Modelos de sistemas en tiempo discreto

Los modelos de sistemas en tiempo discreto son esquemas de representación de filtros digitales. El entorno de cálculo técnico MATLAB^® es compatible con varios modelos de sistemas en tiempo discreto, que se describen en las siguientes secciones:

• Función de transferencia

• Polos, ceros y ganancia

• Espacio de estados

• Expansión en fracciones parciales (forma de residuo)

• Secciones de segundo orden (SOS)

• Estructura de malla

• Matriz de convolución

Función de transferencia

La función de transferencia es una representación básica en el dominio Z de un filtro digital, que expresa el filtro como una relación de dos polinomios. Se trata del principal modelo en tiempo discreto de esta toolbox. La descripción del modelo de la función de transferencia para la transformada Z de la ecuación de diferencia de un filtro digital es

$$Y(z)=\frac{b(1)+b(2)z^{-1}+\dots +b(n+1)z^{-n}}{a(1)+a(2)z^{-1}+\dots +a(m+1)z^{-m}}X(z).$$

En este caso, las constantes b(i) y a(i) son los coeficientes del filtro, y el orden del filtro es el mayor de n y m. En el entorno MATLAB, se almacenan estos coeficientes en dos vectores (vectores fila por convención), un vector fila para el numerador y otro para el denominador. Consulte Filtros y funciones de transferencia para obtener más información sobre la forma de la función de transferencia.

Polos, ceros y ganancia

La forma factorizada o polos, ceros y ganancia de una función de transferencia es

$$H(z)=\frac{q(z)}{p(z)}=k\frac{(z-q(1))(z-q(2))\mathrm{...}(z-q(n))}{(z-p(1))(z-p(2))\mathrm{...}(z-p(n))}.$$

Por convención, los coeficientes de los polinomios se almacenan en vectores fila y las raíces de los polinomios en vectores columna. Por lo tanto, en la forma de polos, ceros y ganancia, las ubicaciones del cero y del polo para el numerador y el denominador de una función de transferencia residen en vectores columna. La ganancia de la función de transferencia factorizada k es un escalar en MATLAB.

Las funciones poly y roots convierten entre representaciones polinómica y de polos, ceros y ganancia. Por ejemplo, un filtro IIR simple es

b = [2 3 4];
a = [1 3 3 1];

Los ceros y polos de este filtro son

q = roots(b)
p = roots(a)
% Gain factor
k = b(1)/a(1)

Volviendo a los polinomios originales,

bb = k*poly(q)
aa = poly(p)

Tenga en cuenta que, en este caso, b y a representan la función de transferencia:

$$H(z)=\frac{2+3z^{-1}+4z^{-2}}{1+3z^{-1}+3z^{-2}+z^{-3}}=\frac{z(2z^2+3z+4)}{z^3+3z^2+3z+1}.$$

En b = [2 3 4], la función roots pierde el cero si z es igual a 0. De hecho, la función pierde los polos y ceros para z igual a 0, siempre que la función de transferencia de entrada tenga más polos que ceros, o viceversa. Esto es aceptable en la mayoría de los casos. Sin embargo, para evitar el problema, basta con añadir ceros para que los vectores tengan la misma longitud antes de utilizar la función roots, por ejemplo, b = [b 0].

Espacio de estados

Siempre se puede representar un filtro digital, o un sistema de ecuaciones de diferencias, como un conjunto de ecuaciones de diferencias de primer orden. En una matriz o forma de espacio de estados, se pueden escribir las ecuaciones como

$$\begin{array}{c}x(n+1)=Ax(n)+Bu(n)\\ y(n)=Cx(n)+Du(n),\end{array}$$

donde u es la entrada, x es el vector de estado e y es la salida. Para los sistemas monocanal, A es una matriz m por m donde m es el orden del filtro, B es un vector columna, C es un vector fila y D es un escalar. La notación del espacio de estados es especialmente conveniente para los sistemas multicanal en los que la entrada u y la salida y se convierten en vectores, y B, C y D se convierten en matrices.

La representación del espacio de estados se extiende fácilmente al entorno MATLAB. A, B, C y D son arreglos rectangulares y las funciones de MATLAB las tratan como variables individuales.

Al tomar la transformada Z de las ecuaciones del espacio de estados y combinarlas, muestra la equivalencia de las formas del espacio de estados y de la función de transferencia:

$$Y(z)=H(z)U(z)\text{, where }H(z)=C{(zI-A)}^{-1}B+D$$

No se preocupe si no está familiarizado con la representación del espacio de estados de los sistemas lineales. Algunos de los algoritmos de diseño de filtros utilizan internamente la forma del espacio de estados, pero precisan conocimientos específicos de los conceptos del espacio de estados para utilizarlos con éxito. Sin embargo, si sus aplicaciones utilizan ampliamente el procesamiento de señales basado en el espacio de estados, consulte el producto Control System Toolbox™, donde encontrará una completa biblioteca de herramientas en materia de espacio de estados.

Expansión en fracciones parciales (forma de residuo)

Cada función de transferencia tiene también su correspondiente representación en forma de expansión en fracciones parciales o residuo, dada por

$$\frac{b(z)}{a(z)}=\frac{r(1)}{1-p(1)z^{-1}}+\mathrm{...}+\frac{r(n)}{1-p(n)z^{-1}}+k(1)+k(2)z^{-1}+\mathrm{...}+k(m-n+1)z^{-(m-n)}$$

siempre que H(z) no tenga polos repetidos. En este caso, n es el grado del polinomio denominador de la función de transferencia racional b(z)/a(z). Si r es un polo de multiplicidad s_r, H(z) tendrá términos de la forma:

$$\frac{r(j)}{1-p(j)z^{-1}}+\frac{r(j+1)}{{(1-p(j)z^{-1})}^2}\mathrm{...}+\frac{r(j+s_r-1)}{{(1-p(j)z^{-1})}^{s_r}}$$

La función Signal Processing Toolbox™ residuez convierte las funciones de transferencia a y desde la forma de expansión de fracción parcial. La “z” al final de residuez hace referencia al dominio z, o dominio discreto. residuez devuelve los polos en un vector columna p, los residuos correspondientes a los polos en un vector columna r y cualquier parte impropia de la función de transferencia original en un vector fila k. residuez determina que dos polos son iguales si la magnitud de su diferencia es menor que el 0,1% de cualquiera de las magnitudes de los polos.

La expansión en fracciones parciales surge en el procesamiento de señales como un método para encontrar la transformada Z inversa de una función de transferencia. Por ejemplo, la expansión en fracciones parciales de

$$H(z)=\frac{-4+8z^{-1}}{1+6z^{-1}+8z^{-2}}$$

es

b = [-4 8];
a = [1 6 8];
[r,p,k] = residuez(b,a)

que corresponde a

$$H(z)=\frac{-12}{1+4z^{-1}}+\frac{8}{1+2z^{-1}}$$

Para hallar la transformada Z inversa de H(z), habrá de dar con la suma de las transformadas Z inversas de los dos sumandos de H(z), dando la respuesta al impulso causal:

$$h(n)=-12{(-4)}^n+8{(-2)}^n,n=0,1,2,\dots$$

Para comprobarlo en el entorno MATLAB, escriba

imp = [1 0 0 0 0];
resptf = filter(b,a,imp)
respres = filter(r(1),[1 -p(1)],imp)+...
  filter(r(2),[1 -p(2)],imp)

Secciones de segundo orden (SOS)

Cualquier función de transferencia H(z) tiene una representación de secciones de segundo orden

$$H(z)={\displaystyle \prod _{k=1}^L{H}_k}(z)={\displaystyle \prod _{k=1}^L\frac{b_{0k}+b_{1k}{z}^{-1}+b_{2k}{z}^{-2}}{a_{0k}+a_{1k}{z}^{-1}+a_{2k}{z}^{-2}}}$$

donde L es el número de secciones de segundo orden que describen el sistema. El entorno MATLAB representa la forma de sección de segundo orden de un sistema de tiempo discreto como un arreglo sos de L por 6. Cada fila de sos contiene una única sección de segundo orden, donde los elementos de la fila son los tres coeficientes del numerador y los tres del denominador que describen la sección de segundo orden.

$$\text{sos}=\left(\begin{array}{llllll}{b}_{01}\hfill & b_{11}\hfill & b_{21}\hfill & a_{01}\hfill & a_{11}\hfill & a_{21}\hfill \\ b_{02}\hfill & b_{12}\hfill & b_{22}\hfill & a_{02}\hfill & a_{12}\hfill & a_{22}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill \\ b_{0L}\hfill & b_{1L}\hfill & b_{2L}\hfill & a_{0L}\hfill & a_{1L}\hfill & a_{2L}\hfill \end{array}\right)$$

Existen muchas formas de representar un filtro en forma de sección de segundo orden. Mediante un cuidadoso emparejamiento de los pares de polos y ceros, la ordenación de secciones en la cascada y el escalado multiplicativo de las secciones, se puede reducir la ganancia de ruido de cuantificación y evitar el desbordamiento en algunas implementaciones de filtros de punto fijo. Las funciones zp2sos y ss2sos, descritas en Linear System Transformations, realizan el emparejamiento de polos y ceros, el escalado de secciones y el ordenamiento de secciones.

Nota

Todas las transformaciones de sección de segundo orden de Signal Processing Toolbox se aplican solo a los filtros digitales.

Estructura de malla

Para un filtro discreto de N-ésimo orden, todos los polos o todos los ceros descritos por los coeficientes polinómicos a(n), n = 1, 2,... , N+1 hay N coeficientes de estructura de malla correspondientes k(n), n = 1, 2,... , N. Los parámetros k(n) también se denominan coeficientes de reflexión del filtro. Con estos coeficientes de reflexión, se puede implementar un filtro discreto como se muestra a continuación.

Diagramas de estructura de malla de los filtros FIR e IIR

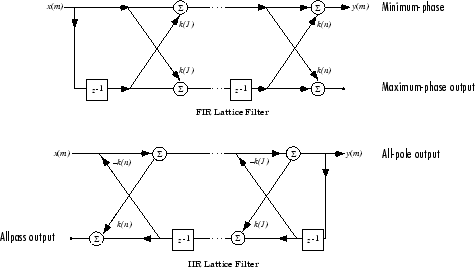
Para un filtro IIR general de polos y ceros descritos por coeficientes polinómicos a y b, hay coeficientes de malla k(n) para el denominador a y coeficientes en escalera v(n) para el numerador b. El filtro de malla/escalera puede implementarse como

Diagrama del filtro de malla/escalera

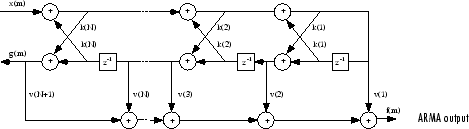
La función tf2latc de la toolbox acepta un filtro FIR o IIR en forma polinómica y devuelve los coeficientes de reflexión correspondientes. Un ejemplo de filtro FIR en forma polinómica es

b = [1.0000   0.6149   0.9899   0.0000   0.0031  -0.0082];

La representación de la malla (coeficiente de reflexión) de este filtro es

k = tf2latc(b)

En el caso de los filtros IIR, la magnitud de los coeficientes de reflexión permite comprobar fácilmente la estabilidad. Si todos los coeficientes de reflexión correspondientes a un polinomio tienen una magnitud menor que 1, todas las raíces de ese polinomio se encontrarán dentro del círculo de la unidad. Por ejemplo, si tenemos en cuenta un filtro IIR con el polinomio del numerador b por arriba y el polinomio del denominador:

a = [1 1/2 1/3];

La representación de malla del filtro es

[k,v] = tf2latc(b,a);  

Como abs(k) < 1 para todos los coeficientes de reflexión de k, el filtro es estable.

La función latc2tf calcula los coeficientes polinómicos de un filtro a partir de sus coeficientes de malla (reflexión). Dado el vector de coeficientes de reflexión k, la forma polinómica correspondiente es

b = latc2tf(k);

Los coeficientes de malla/escalera pueden utilizarse para implementar el filtro mediante la función latcfilt.

Matriz de convolución

En el procesamiento de señales, la convolución de dos vectores o matrices equivale a filtrar uno de los operandos de entrada por el otro. Esta relación permite representar un filtro digital como una matriz de convolución.

Dado cualquier vector, la función convmtx de la toolbox genera una matriz cuyo producto interior con otro vector es equivalente a la convolución de los dos vectores. La matriz generada representa un filtro digital que se puede aplicar a cualquier vector de longitud apropiada; la dimensión interna de los operandos debe coincidir para calcular el producto interno.

La matriz de convolución de un vector b, que representa los coeficientes del numerador de un filtro digital, es

b = [1 2 3];
x = randn(3,1);
C = convmtx(b',3);

Las siguientes son dos formas equivalentes de convolucionar b con x.

y1 = C*x;
y2 = conv(b,x);