La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

Distribución chi-cuadrado

Visión general

La distribución chi-cuadrado (χ²) es una familia de curvas de un parámetro. La distribución chi-cuadrado se utiliza habitualmente en la comprobación de hipótesis, en particular en la prueba de bondad de ajuste de chi-cuadrado.

Statistics and Machine Learning Toolbox™ ofrece varias formas de trabajar con la distribución chi-cuadrado.

• Utilice funciones específicas de la distribución (chi2cdf, chi2inv, chi2pdf, chi2rnd y chi2stat) con parámetros de distribución especificados. Las funciones específicas de la distribución pueden aceptar parámetros de varias distribuciones chi-cuadrado.

• Utilice funciones de distribución genéricas (cdf, icdf, pdf, random) con un nombre de distribución específico ('Chisquare') y parámetros.

Parámetros

La distribución chi-cuadrado utiliza el siguiente parámetro.

Parámetro	Descripción	Soporte
nu (ν)	Grados de libertad	ν = 1, 2, 3,...

El parámetro de grados de libertad suele ser un número entero, pero las funciones chi-cuadrado aceptan cualquier valor positivo.

La suma de dos variables aleatorias chi-cuadrado con grados de libertad de ν₁ y ν₂ es una variable aleatoria chi-cuadrado con grados de libertad de ν = ν₁ + ν₂.

Función de densidad de probabilidad

La función de densidad de probabilidad (pdf) de la distribución chi-cuadrado es

$$y=f\left(x|\nu \right)=\frac{x^{\left(\nu -2\right)/2}{e}^{-x/2}}{2^{\frac{\nu }{2}}\Gamma \left(\nu /2\right)},$$

donde ν son los grados de libertad, y Γ( · ) es la función gamma.

Para ver un ejemplo, consulte Calcular la pdf de una distribución chi-cuadrado.

Función de distribución acumulativa

La función de distribución acumulativa (cdf) de la distribución chi-cuadrado es

$$p=F(x|\nu )={\displaystyle {\int }_0^x\frac{t^{(\nu -2)/2}{e}^{-t/2}}{2^{\nu /2}\Gamma (\nu /2)}dt},$$

, donde ν son los grados de libertad y Γ( · ) es la función gamma. El resultado p es la probabilidad de que una sola observación a partir de la distribución chi-cuadrado con ν grados de libertad se incluya en el intervalo [0, x].

Para ver un ejemplo, consulte Calcular la cdf de una distribución chi-cuadrado.

Función de distribución acumulativa inversa

La función de distribución acumulativa inversa (icdf) de la distribución chi-cuadrado es

$$x=F^{-1}(p|\nu )=\{x:F(x|\nu )=p\},$$

donde

$$p=F(x|\nu )={\displaystyle {\int }_0^x\frac{t^{(\nu -2)/2}{e}^{-t/2}}{2^{\nu /2}\Gamma (\nu /2)}}dt,$$

ν son los grados de libertad, y Γ( · ) es la función gamma. El resultado p es la probabilidad de que una sola observación a partir de la distribución chi-cuadrado con ν grados de libertad se incluya en el intervalo [0, x].

Estadística descriptiva

La media de la distribución chi-cuadrado es ν.

La varianza de la distribución chi-cuadrado es 2ν.

Ejemplos

Calcular la pdf de una distribución chi-cuadrado

Calcule la pdf de una distribución chi-cuadrado con 4 grados de libertad.

x = 0:0.2:15;
y = chi2pdf(x,4);

Represente la pdf.

figure;
plot(x,y)
xlabel('Observation')
ylabel('Probability Density')

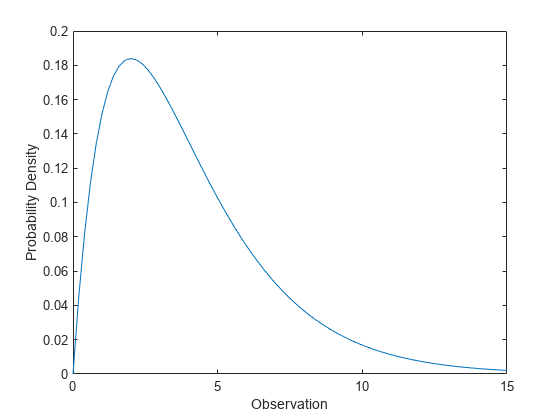
La distribución chi-cuadrado está sesgada a la derecha, especialmente cuando hay pocos grados de libertad.

Calcular la cdf de una distribución chi-cuadrado

Calcule la cdf de una distribución chi-cuadrado con 4 grados de libertad.

x = 0:0.2:15;
y = chi2cdf(x,4);

Represente la cdf.

figure;
plot(x,y)
xlabel('Observation')
ylabel('Cumulative Probability')

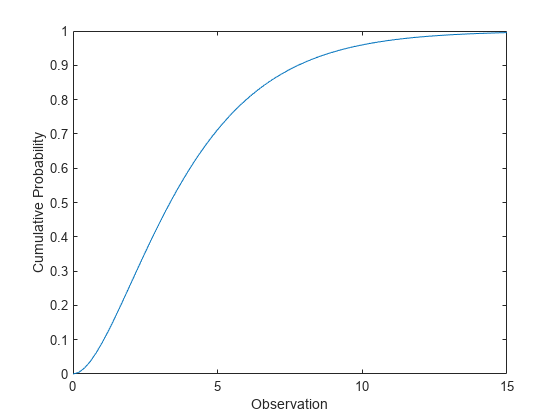
Distribuciones relacionadas

• F Distribution: la distribución F es una distribución de dos parámetros que tiene los parámetros ν₁ (grados de libertad del numerador) y ν₂ (grados de libertad del denominador). La distribución F puede definirse como el cociente $$F=\frac{\raisebox{1ex}{${\chi }_1^2$}\!\left/ \!\raisebox{-1ex}{${\nu }_1$}\right.}{\raisebox{1ex}{${\chi }_2^2$}\!\left/ \!\raisebox{-1ex}{${\nu }_2$}\right.}$$, donde χ²₁ y χ²₂ son ambas distribuciones chi-cuadrado con ν₁ y ν₂ grados de libertad, respectivamente.

• Distribución gamma: la distribución gamma es una distribución continua de dos parámetros que tiene los parámetros a (forma) y b (escala). La distribución chi-cuadrado es igual a la distribución gamma con 2a = ν y b = 2.

• Noncentral Chi-Square Distribution: la distribución chi-cuadrado no central es una distribución continua de dos parámetros que tiene los parámetros ν (grados de libertad) y δ (no centralidad). La distribución chi-cuadrado no central es igual a la distribución chi-cuadrado cuando δ = 0.

• Distribución normal — La distribución normal es una distribución continua de dos parámetros que tiene los parámetros μ (media) y σ (desviación estándar). La distribución normal estándar se produce cuando μ = 0 y σ = 1.

  Si Z₁, Z₂, …, Z_n son variables aleatorias normales estándar, $${\displaystyle \sum _{i=1}^n{Z}_i{}^2}$$ tiene una distribución chi-cuadrado con grados de libertad de ν = n – 1.

  Si un conjunto de n observaciones está distribuido normalmente con la varianza σ² y s² es la varianza de la muestra, $$\frac{\left(n-1\right)s^2}{{\sigma }^2}$$ tiene una distribución chi-cuadrado con grados de libertad de ν = n – 1. Esta relación se utiliza para calcular intervalos de confianza para la estimación del parámetro normal σ² en la función normfit.

• Distribución t de Student: la distribución t de Student es una distribución continua de un parámetro que tiene el parámetro ν (grados de libertad). Si Z tiene una distribución normal estándar y χ² tiene una distribución chi-cuadrado con grados de libertad de ν, $$\text{t = }\frac{Z}{\sqrt{{\chi }^2/\nu }}$$ tiene una distribución t de Student con grados de libertad de ν.

• Wishart Distribution: la distribución de Wishart es un análogo de mayor dimensión de la distribución chi-cuadrado.

Referencias

[1] Abramowitz, Milton, and Irene A. Stegun, eds. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables. 9. Dover print.; [Nachdr. der Ausg. von 1972]. Dover Books on Mathematics. New York, NY: Dover Publ, 2013.

[2] Devroye, Luc. Non-Uniform Random Variate Generation. New York, NY: Springer New York, 1986. https://doi.org/10.1007/978-1-4613-8643-8

[3] Evans, M., N. Hastings, and B. Peacock. Statistical Distributions. 2nd ed., Hoboken, NJ: John Wiley & Sons, Inc., 1993.

[4] Kreyszig, Erwin. Introductory Mathematical Statistics: Principles and Methods. New York: Wiley, 1970.

Consulte también

chi2cdf | chi2pdf | chi2inv | chi2stat | chi2gof | chi2rnd

Temas relacionados

• Working with Probability Distributions
• Distribuciones admitidas