allmargin
Gain margin, phase margin, delay margin, and crossover frequencies
Description
S = allmargin(L)L. The negative feedback loop is computed as
feedback(L,eye(M)), where M is the number
of inputs and outputs in L.
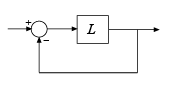
For a MIMO system, allmargin returns loop-at-a-time stability
margins for the negative-feedback closed loop system. Use
allmargin to find classical margins of any SISO or MIMO
model, including models with delays.
S = allmargin(L,Focus=[fmin,fmax])fmin,fmax], ignoring stability issues
outside this range. For instance, use this syntax to ignore very low frequency
dynamics for the purpose of computing stability margins. (since R2024a)
Examples
Input Arguments
Output Arguments
Tips
allmarginassumes that the system with open-loop responseLis a negative-feedback system. To compute the classical stability margins of the positive feedback systemfeedback(L,eye(M),+1), useallmargin(-L).To compute classical margins for a system modeled in Simulink®, first linearize the model to obtain the open-loop response at a particular operating point. Then, use
allmarginto compute classical stability margins for the linearized system. For more information, see Stability Margins of a Simulink Model (Robust Control Toolbox).If you have Robust Control Toolbox™ software, you can use
diskmargin(Robust Control Toolbox) to compute disk-based margins that define a range of "safe" gain and phase variations for which the feedback loop remains stable.
Version History
Introduced before R2006aSee Also
Linear System Analyzer | margin | diskmargin (Robust Control Toolbox)
Topics
- Stability Margins of a Simulink Model (Robust Control Toolbox)