initial

Respuesta del sistema al modelo de espacio de estados inicial

Sintaxis

initial(sys,x0)

initial(sys,x0,tFinal)

initial(sys,x0,t)

initial(sys1,sys2,...,sysN,x0,___)

initial(sys1,LineSpec1,...,sysN,LineSpecN,x0,___)

[y,tOut,x] = initial(sys,x0)

[y,tOut,x] = initial(sys,x0,___)

Descripción

Gráficas de respuesta inicial

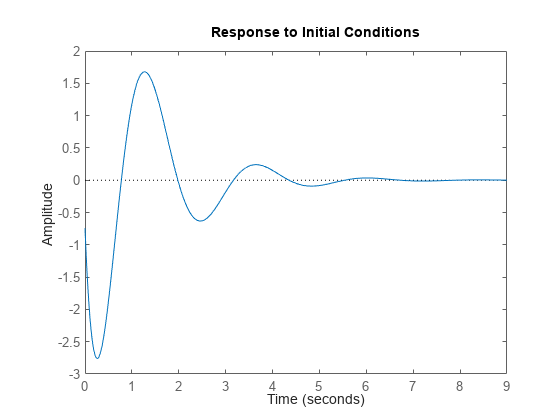
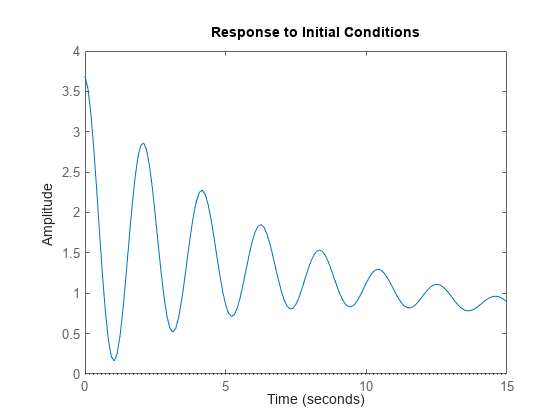
initial(sys,x0) representa la respuesta no forzada del sistema a un modelo de espacio de estados inicial (ss) sys con una condición inicial de los estados que especifica el vector x0:

$$\begin{array}{cc}\dot{x}=Ax,& x(0)=x_0\\ y=Cx& \end{array}$$

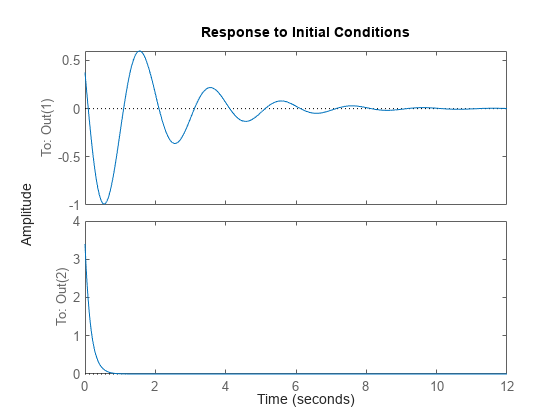
El modelo de espacio de estados sys puede ser de tiempo continuo o discreto, así como SISO o MIMO. En los sistemas de espacio de estados MIMO, la gráfica muestra las respuestas para las salidas de cada canal. initial determina automáticamente las unidades de tiempo y la duración de la simulación en función de la dinámica del sistema.

initial(sys,x0,tFinal) representa la respuesta desde t = 0 hasta el tiempo final t = tFinal. La función utiliza la dinámica del sistema para determinar las unidades de tiempo que intervienen.

initial(sys,x0,t) representa la respuesta en los tiempos especificados en el vector t.

initial(sys1,sys2,...,sysN,x0,___) representa la respuesta de varios sistemas dinámicos en la misma gráfica. Todos los sistemas deben contar con el mismo número de entradas y salidas. Puede utilizar varios sistemas dinámicos con cualquiera de las combinaciones de entrada/argumento anteriores.

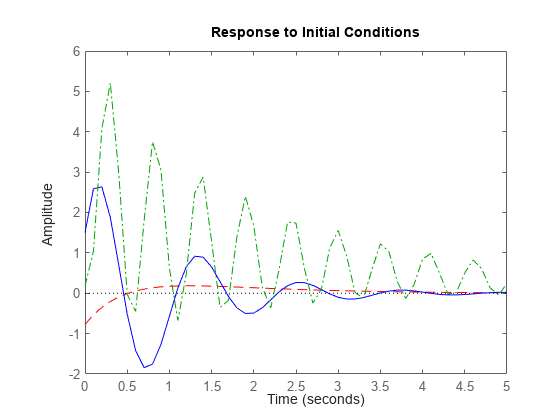
initial(sys1,LineSpec1,...,sysN,LineSpecN,x0,___) especifica un color, un estilo de línea y un marcador para cada sistema de la gráfica de respuesta. Puede utilizar LineSpec con cualquiera de las combinaciones de entrada/argumento anteriores. Cuando necesite opciones de personalización de gráficas adicionales, utilice en su lugar initialplot.

Datos de respuesta inicial

[y,tOut,x] = initial(sys,x0) devuelve la respuesta de salida y, el vector de tiempo tOut y las trayectorias de estado x. El arreglo y tiene tantas filas como muestras de tiempo (longitud de tOut) y tantas columnas como salidas. Del mismo modo, x tiene length(tOut) filas y tantas columnas como estados.

[y,tOut,x] = initial(sys,x0,___) también utiliza el tiempo de respuesta especificado como t o tFinal para devolver los datos de respuesta.

Ejemplos

Gráfica de respuesta a las condiciones iniciales

Para este ejemplo, genere un modelo de espacio de estados aleatorio con 5 estados y cree la gráfica para la respuesta del sistema a los estados iniciales.

rng("default")
sys = rss(5);
x0 = [1,2,3,4,5];
initial(sys,x0)

Respuesta del modelo de espacio de estados a la condición inicial

Represente la respuesta del siguiente modelo de espacio de estados:

$$\begin{array}{rcl}\left[\begin{array}{l}{\underset{}{\overset{\dot{}}{x}}}_1\\ {\underset{}{\overset{\dot{}}{x}}}_2\end{array}\right]& =& \left[\begin{array}{cc}-0.5572& -0.7814\\ 0.7814& 0\end{array}\right]\left[\begin{array}{l}{x}_1\\ x_2\end{array}\right]\\ y& =& \left[\begin{array}{cc}1.9691& 6.4493\end{array}\right]\left[\begin{array}{l}{x}_1\\ x_2\end{array}\right].\end{array}$$

Utilice la siguiente condición inicial:

$$x(0)=\left[\begin{array}{l}1\\ 0\end{array}\right].$$

a = [-0.5572, -0.7814; 0.7814, 0];
c = [1.9691  6.4493];
x0 = [1 ; 0];

sys = ss(a,[],c,[]);
initial(sys,x0)

Gráfica de respuesta a la condición inicial del sistema MIMO

Considere el siguiente sistema dinámico de dos entradas y dos salidas.

$$sys(s)=\left[\begin{array}{cc}0& {\displaystyle \frac{3s}{s^2+s+10}}\\ {\displaystyle \frac{s+1}{s+5}}& {\displaystyle \frac{2}{s+6}}\end{array}\right].$$

Convierta el modelo sys al formato de espacio de estados dado que las gráficas de respuesta a la condición inicial se admiten únicamente para modelos de espacio de estados.

sys = ss([0, tf([3 0],[1 1 10]) ; tf([1 1],[1 5]), tf(2,[1 6])]);
size(sys)

State-space model with 2 outputs, 2 inputs, and 4 states.

El modelo de espacio de estados resultante tiene cuatro estados. Por tanto, proporcione un vector de la condición inicial con cuatro elementos.

x0 = [0.3,0.25,1,4];

Cree la gráfica de respuesta a la condición inicial.

initial(sys,x0);

La gráfica resultante contiene dos subgráficas, una para cada salida de sys.

Gráfica de respuesta a las condiciones iniciales en un tiempo especificado

Para este ejemplo, examine la respuesta a la condición inicial del siguiente modelo cero-polo-ganancia y limite la gráfica a tFinal = 15 s.

En primer lugar, convierta el modelo zpk a un modelo ss, dado que initial solo admite modelos de espacio de estados.

sys = ss(zpk(-1,[-0.2+3j,-0.2-3j],1)*tf([1 1],[1 0.05]));
tFinal = 15;
x0 = [4,2,3];

Ahora, cree la gráfica de respuesta a las condiciones iniciales.

initial(sys,x0,tFinal);

Respuestas a la condición inicial de varios sistemas

Para este ejemplo, represente las respuestas a la condición inicial de los tres sistemas dinámicos.

En primer lugar, cree los tres modelos y proporcione las condiciones iniciales. Todos los sistemas deberían contar con el mismo número de estados.

rng('default');
sys1 = rss(4); 
sys2 = rss(4);
sys3 = rss(4);
x0 = [1,1,1,1];

Represente las respuestas a la condición inicial de los tres modelos con el vector de tiempo t que abarca 5 segundos.

t = 0:0.1:5;
initial(sys1,'r--',sys2,'b',sys3,'g-.',x0,t)

Datos de respuesta a la condición inicial del modelo de espacio de estados

Extraiga los datos de respuesta a la condición inicial del siguiente modelo de espacio de estados con dos estados:

$$\begin{array}{rcl}\left[\begin{array}{l}{\underset{}{\overset{\dot{}}{x}}}_1\\ {\underset{}{\overset{\dot{}}{x}}}_2\end{array}\right]& =& \left[\begin{array}{cc}-0.5572& -0.7814\\ 0.7814& 0\end{array}\right]\left[\begin{array}{l}{x}_1\\ x_2\end{array}\right]\\ y& =& \left[\begin{array}{cc}1.9691& 6.4493\end{array}\right]\left[\begin{array}{l}{x}_1\\ x_2\end{array}\right].\end{array}$$

Utilice las siguientes condiciones iniciales:

$$x(0)=\left[\begin{array}{l}1\\ 0\end{array}\right].$$

a = [-0.5572, -0.7814; 0.7814, 0];
c = [1.9691  6.4493];
x0 = [1 ; 0];
sys = ss(a,[],c,[]);
[y,tOut,x] = initial(sys,x0);

El arreglo y tiene tantas filas como muestras de tiempo (longitud de tOut) y tantas columnas como salidas. Del mismo modo, x tiene tantas filas como muestras de tiempo (longitud de tOut) y tantas columnas como estados.

Datos de respuesta a la condición con tiempo especificado

Para este ejemplo, extraiga los datos de respuesta a la condición inicial de un modelo con 6 estados, 3 salidas y 2 entradas.

En primer lugar, cree el modelo y proporcione las condiciones iniciales.

rng('default');
sys = rss(6,3,2); 
x0 = [0.1,0.3,0.05,0.4,0.75,1];

Extraiga las respuestas a la condición inicial del modelo con el vector de tiempo t que abarca 15 segundos.

t = 0:0.1:15;
[y,tOut,x] = initial(sys,x0,t);

El arreglo y tiene tantas filas como muestras de tiempo (longitud de tOut) y tantas columnas como salidas. Del mismo modo, x tiene tantas filas como muestras de tiempo (longitud de tOut) y tantas columnas como estados.

Argumentos de entrada

sys — Sistema dinámico

modelo de sistema dinámico | arreglo de modelos

Sistema dinámico, especificado como un modelo de sistema dinámico SISO o MIMO, o bien un arreglo de modelos de sistemas dinámicos. Puede utilizar únicamente modelos de espacio de estados de los siguientes tipos:

• Modelos numéricos de tiempo continuo o de tiempo discreto ss.

• Modelos LTI generalizados o con incertidumbre, como modelos genss o uss. El uso de modelos con incertidumbre requiere el software Robust Control Toolbox™.

  • En el caso de los bloques de diseño de control ajustables, la función evalúa el modelo con su valor actual tanto para representar como para devolver los datos de respuesta.

  • En el caso de los bloques de diseño de control con incertidumbre, la función representa el valor nominal y muestras aleatorias del modelo. Cuando utiliza argumentos de salida, la función devuelve únicamente datos de respuesta para el modelo nominal.

• Modelos dispersos de espacio de estados, como modelos sparss y mechss. Debe especificar el tiempo final tFinal para los modelos dispersos de espacio de estados.

Si sys es un arreglo de modelos, la función representa las respuestas de todos los modelos del arreglo en los mismos ejes.

tFinal — Tiempo final para calcular la respuesta

escalar positivo

Tiempo final para calcular la respuesta, especificado como un valor escalar positivo. initial simula la respuesta desde t = 0 hasta t = tFinal.

• En el caso de los sistemas de tiempo continuo, la función determina automáticamente el tamaño en escalón y el número de puntos a partir de la dinámica del sistema. Exprese tFinal en las unidades de tiempo del sistema, especificadas en la propiedad TimeUnit de sys.

• En el caso de los sistemas de tiempo discreto, la función utiliza el tiempo de muestreo de sys como tamaño en escalón. Exprese tFinal en las unidades de tiempo del sistema, especificadas en la propiedad TimeUnit de sys.

• Para sistemas de tiempo discreto con tiempo de muestreo no especificado (Ts = -1), initial interpreta tFinal como el número de períodos de muestreo que simular.

t — Vector de tiempo

vector

Vector de tiempo en el que se desea calcular la respuesta, especificado como un vector de valores escalares positivos. Exprese t en las unidades de tiempo del sistema, especificadas en la propiedad TimeUnit de sys.

• En el caso de modelos de tiempo continuo, especifique t en formato Ti:dt:Tf. Para obtener la respuesta en cada unidad de tiempo, la función utiliza dt como tiempo de muestreo de una aproximación discreta al sistema continuo.

• En el caso de modelos de tiempo discreto, especifique t en formato Ti:Ts:Tf, donde Ts es el tiempo de muestreo de sys.

initial aplica siempre la entrada en t = 0, independientemente de Ti.

LineSpec — Estilo de línea, marcador y color

vector de caracteres | cadena

Estilo de línea, marcador y color, especificados como una cadena o vector de uno, dos o tres caracteres. Los caracteres pueden aparecer en cualquier orden. No es necesario que especifique las tres características (estilo de línea, marcador y color). Por ejemplo, si omite el estilo de línea y especifica el marcador, la gráfica mostrará únicamente el marcador y ninguna línea. Para obtener más información sobre cómo configurar este argumento, consulte el argumento de entrada LineSpec de la función plot.

Ejemplo: 'r--' especifica una línea discontinua roja

Ejemplo: '*b' especifica marcadores de asterisco azul

Ejemplo: 'y' especifica una línea amarilla

x0 — Condición inicial de los estados

vector

Condición inicial de los estados, especificada como un vector. x0 debe tener la misma longitud que el número de estados en sys.

Argumentos de salida

y — Datos de respuesta

arreglo

Datos de respuesta, devueltos como un arreglo.

• En los sistemas SISO, y es un vector columna de la misma longitud que t (si se indica) o tOut (si no se indica t).

• En los sistemas de una entrada y varias salidas, y es una matriz con tantas filas como muestras de tiempo y tantas columnas como salidas. Así, la j-ésima columna de y, o y(:,j), contiene la respuesta desde la entrada hasta la j-ésima salida.

• En los sistemas MIMO, las dimensiones de y son N por Ny, donde:

  • N es el número de muestras de tiempo.

  • Ny es el número de salidas del sistema.

tOut — Tiempos en los que se calcula la respuesta

vector

Tiempos en los que se calcula la respuesta, devueltos como un vector. Cuando no proporciona un vector específico t de tiempos, initial elige este vector de tiempo en función de la dinámica del sistema. Los tiempos se expresan en las unidades de tiempo de sys.

x — Trayectorias de estado

arreglo

Trayectorias de estado, devueltas como un arreglo. x contiene la evolución de los estados de sys en cada tiempo de t o tOut. Las dimensiones de x son N por Nx, donde:

• N es el número de muestras de tiempo.

• Nx es el número de estados.

Historial de versiones

Introducido antes de R2006a

Consulte también

initialplot | impulse | lsim | Linear System Analyzer | step

Temas

• Formas de personalizar gráficas
• Response from Initial Conditions

×

Abrir ejemplo

Tiene una versión modificada de este ejemplo. ¿Desea abrir este ejemplo con sus modificaciones?

No, sobrescribir la versión modificada Sí