Pressure Compensator Valve (TL)
Libraries:
Simscape /
Fluids /
Thermal Liquid /
Valves & Orifices /
Pressure Control Valves
Description
The Pressure Compensator Valve (TL) block represents a pressure compensator in a thermal liquid network, such as a pressure relief valve or pressure reducing valve. Use this block to maintain the pressure at the valve based on signals from another part of the system.
The pressure differential between ports X and Y is the control pressure, Pcontrol. When this value meets or exceeds the set pressure, the valve area opens or closes depending on the Valve specification parameter. The pressure regulation range begins at the set pressure, Pset.
Pressure Control
The block regulates pressure when Pcontrol exceeds Pset. The block continues to regulate the pressure up to Pmax, the sum of Pset and the pressure regulation range. The block supports two modes of regulation:
When you set Set pressure control to
Controlledand connect a pressure signal to port Ps, the block keeps the pressure regulation range constant. The valve regulates pressure when Pcontrol is greater than the value of the signal at port Ps and less than Pmax.When you set Set pressure control to
Constant, the Set pressure differential parameter defines a constant set pressure.
Conservation of Mass
The block conserves mass such that
The block calculates the mass flow rate through the valve as
where:
Cd is the value of the Discharge coefficient parameter.
Avalve is the instantaneous valve open area.
Aport is the value of the Cross-sectional area at ports A and B parameter.
is the average fluid density.
Δp is the valve pressure difference pA – pB.
The critical pressure difference, Δpcrit, is the pressure differential specified by the Critical Reynolds number parameter, Recrit. This parameter represents the flow regime transition point between laminar and turbulent flow. The block finds the critical pressure difference as
where μ is the dynamic viscosity of the thermal liquid.
The pressure loss, PRloss, describes the reduction of pressure in the valve due to a decrease in area. The block calculates the pressure loss as:
The pressure recovery describes the positive pressure change in the valve due to an increase in area. When you clear the Pressure recovery check box, the block sets PRloss to 1.
The block calculates Avalve using the opening parameterization and the valve opening dynamics.
Valve Opening Parameterization
When you set Opening parameterization to
Linear, the valve area for normally open valves is
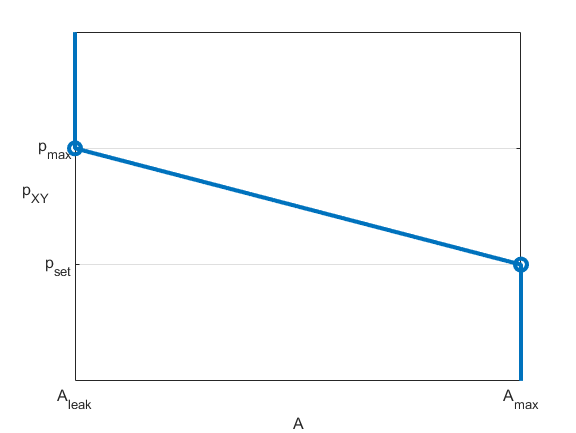
where Aleak is the value of the Leakage Area parameter and Amax is the value of the Maximum opening area parameter. This figure shows how the block controls the opening area for a normally open valve using the linear parameterization.
For normally closed valves, the block uses
This figure show how the block controls the opening area for a normally closed valve using the linear parameterization.

The normalized pressure, , is
When the valve is in a near-open or near-closed position in the linear parameterization, you can maintain numerical robustness in your simulation by adjusting the Smoothing factor parameter. If the Smoothing factor parameter is nonzero, the block smoothly saturates the control pressure between pset and pmax. For more information, see Numerical Smoothing.
When you set Opening parameterization to
Tabulated, Aleak and
Amax are the first and last parameters of the
Opening area vector parameter, respectively. The block calculates the
opening area as
where:
pcontrol,TLU,ref = pTLU + poffset.
pTLU is the Pressure differential vector parameter.
poffset is an internal pressure offset that causes the valve to start closing when pcontrol,TLU,ref = pset.
ATLU is the Opening area vector parameter.
This figure demonstrates how the block controls the opening area for a normally open valve using the tabulated data parameterization.
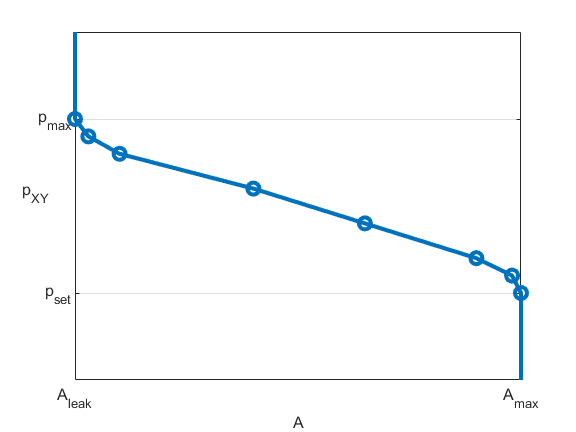
This figure demonstrates how the block controls the opening area for a normally closed valve using the tabulated data parameterization.

Opening Dynamics
When you select Opening dynamics, the block introduces a control pressure lag where pcontrol becomes the dynamic control pressure, pdyn. The block calculates the instantaneous change in dynamic control pressure based on the Opening time constant parameter, τ:
By default, the block clears the Opening dynamics
check box. When Opening parameterization is
Linear, a nonzero value for the Smoothing
factor parameter provides additional numerical stability when the orifice is in
near-closed or near-open position.
The block calculates the steady-state dynamics according to the Opening parameterization parameter based on the control pressure, pcontrol.
Energy Balance
The energy conservation equation in the valve is
where:
ϕA is the energy flow rate into the valve through port A.
ϕB is the energy flow rate into the valve through port B.
Faults
To model a fault, in the Faults section, click the Add fault hyperlink next to the fault that you want to model. Use the fault parameters to specify the fault properties. For more information about fault modeling, see Introduction to Simscape Faults.
You can set the Opening area when faulted parameter to:
Closed— The valve area stops at its smallest value, depending on the Opening parameterization parameter setting:Linear— The valve area stops at the value of the Leakage area parameter.Tabulated— The valve area stops at the smallest element of the Opening area vector parameter.
Open— The valve stops at its largest value, depending on the Opening parameterization parameter setting:Linear— The valve area stops at the value of the Maximum opening area parameter.Tabulated— The valve area stops at the largest element of the Opening area vector parameter.
Maintain last value— The valve area stops at the valve open area when the trigger occurred.
Due to numerical smoothing at the extremes of the valve area, the minimum area the block uses is larger than the leakage area, and the maximum is smaller than the value of the Maximum orifice area parameter. This effect is in proportion to the amount of smoothing you apply.
After the fault triggers, the valve remains at the faulted area for the rest of the simulation.
