Modelar una pelota que rebota en tiempo continuo
Este ejemplo muestra cómo configurar un gráfico de Stateflow® que simula una pelota que rebota en tiempo continuo. La pelota se mueve continuamente por el aire hasta que toca el suelo, momento en el que se produce una discontinuidad. Como resultado, la pelota cambia de velocidad y de dirección repentinamente. Para obtener más información, consulte Continuous-Time Modeling in Stateflow.
El modelo sf_bounce contiene un gráfico que se actualiza en tiempo continuo. Las variables locales describen la dinámica de una pelota en caída libre en términos de posición y velocidad. Durante la simulación, el modelo utiliza la detección de cruce por cero para determinar cuándo la pelota toca el suelo.
Dinámica de una pelota que rebota
Puede especificar cómo una pelota cae en caída libre por la fuerza de la gravedad en términos de posición p y velocidad v con este sistema de ecuaciones diferenciales de primer orden:
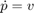
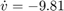
Cuando p <= 0, la pelota toca el suelo y rebota. Puede modelar el rebote actualizando la posición y la velocidad de la pelota:
Restablezca la posición a p = 0.
Restablezca la velocidad al negativo de su valor justo antes de que la pelota toque el suelo.
Para tener en cuenta la pérdida de energía, multiplique la velocidad nueva por un coeficiente de distribución (-0.8).
Configurar un gráfico para una simulación en tiempo continuo
En el modelo, el gráfico BouncingBall implementa la lógica modal para simular la dinámica continua de la caída libre y los cambios discretos asociados al rebote. En el cuadro de diálogo de propiedades del gráfico, esta configuración permite que el gráfico BouncingBall simule en tiempo continuo:
Update method es
Continuous, por lo que el gráfico utiliza simulación en tiempo continuo para modelar la dinámica de la pelota que rebota.Enable zero-crossing detection está seleccionado, por lo que el solver de Simulink® puede determinar exactamente cuándo la pelota toca el suelo. De lo contrario, el modelo de Simulink no puede simular la física de forma exacta y parece que la pelota sigue descendiendo por debajo del suelo.
Definir variables de tiempo continuo
El gráfico BouncingBall tiene dos variables de tiempo continuo: p para posición y v para velocidad. Para cada una de estas variables:
Scope es
Local.Type es
double.Update Method es
Continuous.
Para exponer el estado continuo del gráfico al modelo de Simulink, el gráfico BouncingBall tiene dos variables de salida: p_out y v_out. Para cada una de estas variables:
Scope es
Output.Type es
double.Update Method es
Discrete.
El gráfico define la derivada de tiempo de variables de tiempo continuo implícitamente:
p_dotes la derivada de la posiciónp.v_dotes la derivada de la velocidadv.
En Model Explorer, puede ver las variables locales de tiempo continuo y las correspondientes salidas en el gráfico. Las variables de derivadas implícitas no aparecen en Model Explorer ni en el panel Symbols.

Modelar la dinámica continua de una caída libre
El gráfico BouncingBall consta de un estado único denominado Falling que resuelve numéricamente las ecuaciones diferenciales de la caída libre. La transición predeterminada al estado establece la posición inicial en 10 m y la velocidad inicial en 15 m/s. Las acciones during del estado:
Definen las derivadas de la posición y la velocidad
Asignan los valores de la posición y velocidad de la pelota a las variables de salida
p_outyv_out

Modelar efectos discretos del rebote
El estado Falling tiene una transición de autobucle que modela la discontinuidad del rebote como un cambio de modo instantáneo cuando la pelota cambia de dirección repentinamente. La condición en la transición llama al operador de detección de flancos falling. Este operador determina cuándo la pelota toca el suelo detectando el momento en el que la posición supera un umbral de cero y se convierte en negativa. Si la condición es válida, la acción de condición restablece la posición y velocidad cuando la pelota toca el suelo.
Validar la semántica de un gráfico
El gráfico BouncingBall cumple los requisitos de diseño definidos en Guidelines for Continuous-Time Simulation. En particular, el gráfico:
Inicializa las variables locales p y v en la transición predeterminada
Asigna valores a las derivadas p_dot y v_dot en una acción
duringEscribe en las variables locales p y v en una acción de transición
No contiene eventos, transiciones internas, lógica temporal basada en eventos u operadores de detección de cambios
Ver los resultados de la simulación
Después de ejecutar el modelo, el bloque Scope representa la posición y la velocidad de la pelota. La gráfica de la posición muestra el patrón de rebote esperado.
