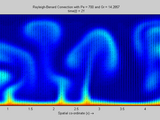
Rayleigh Benard Convection
Natural convection due to thermal gradients are simulated in a 2D rectangular domain. The Navier-Stokes equations are solved by the pressure projection method on a staggered grid. The hyperbolic flux terms are discretized explicitly (CD, MacCormack and Richtmyer) while the diffusive terms are dealt with both explicitly and implicitly. The energy transport equation is explicitly discretized (CD) for the advective fluxes along with an option for implicit or explicit method for the conduction terms. The Pressure Poisson equation is solved implicitly. The top and bottom surfaces are isothermal while the sides are adiabatic. No-slip is enforced for velocity on all sides and homogenous boundary conditions are employed for pressure. Both velocity and temperature field are used for visualization purposes. For specific (critical) values of Pe,Gr and Re, Rayleigh Benard convective rolls are observed.
Citar como
Suraj Shankar (2024). Rayleigh Benard Convection (https://www.mathworks.com/matlabcentral/fileexchange/38093-rayleigh-benard-convection), MATLAB Central File Exchange. Recuperado .
Compatibilidad con la versión de MATLAB
Compatibilidad con las plataformas
Windows macOS LinuxCategorías
Etiquetas
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Descubra Live Editor
Cree scripts con código, salida y texto formateado en un documento ejecutable.
| Versión | Publicado | Notas de la versión | |
|---|---|---|---|
| 1.0.0.0 |