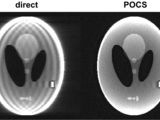
MRI Partial Fourier reconstruction with POCS
POCS (Projection Onto Convex Sets) is often used to reconstruct partial Fourier MRI data.
This implementation works with 2D or 3D data on a Cartesian grid. It is optimized for speed and automatically detects the asymmetrically sampled dimension.
Input data is generally assumed to be a multi-channel k-space signal, with the first dimension for the channels (or coils). You can, however, pass a pure 2D array.
[im, kspFull] = pocs( kspIn, iter, watchProgr )
=== Input ===
kspIn: Reduced Cartesian MRI Data-Set
Any dimension may be reduced,
but only one reduction dim. is allowed due to Physics/Math.
Allowed shapes for kspIn are...
... Ny x Nx
... Nc x Ny x Nx
... Nc x Ny x Nx x Nz
With Nc == number of receive Channels / Coils.
kspIn can either be a zero-padded array, so the partial Fourier property is obvious.
Or kspIn can be the measured data only, then we try to find k-space centre automagically
and create a zero-padded array with the full size, first.
Errors are however more likely to occur in the latter case.
iter: No. of iterations
(optional) default: iter = 20
Try on your own if larger iter improves your results!
watchProgr: true/false; Whether the progress of the reconstruction should
(optional) be monitored in an image window.
In 3D data, only the central partition will be shown.
=== Output ===
im: Reconstructed Images (channels not combined)
kspFull: Reconstructed full k-space data (just the Fourier transformed im)
Citar como
Michael Völker (2024). MRI Partial Fourier reconstruction with POCS (https://www.mathworks.com/matlabcentral/fileexchange/39350-mri-partial-fourier-reconstruction-with-pocs), MATLAB Central File Exchange. Recuperado .
Compatibilidad con la versión de MATLAB
Compatibilidad con las plataformas
Windows macOS LinuxCategorías
- Sciences > Neuroscience > Human Brain Mapping > MRI >
Etiquetas
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Descubra Live Editor
Cree scripts con código, salida y texto formateado en un documento ejecutable.