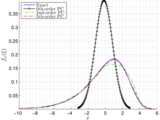
Polynomial chaos approximation
The main file 'PC_examples_1D.m' contains basic examples, in which several probability distributions are approximated using the polynomial chaos (PC) expansion. The key components of this method lie in the calculation of the orthogonal polynomials and the computation of the PC coefficients:
i). Functions to compute N-dimensional Hermite, Charlier and Jacobi polynomial are provided; extension to other types of orthogonal polynomials is straightforward.
ii). The PC coefficients are estimated using the projection method, where the integral is solved using a Gauss-Hermite quadrature. This step was only programmed for the case of 1D Hermite polynomials. Therefore, further extension to other types of orthogonal polynomials is required. An implementation of the regression method for the estimation of the PC coefficients can deal with this problem (hopefully, it will be included in a future version).
Citar como
Felipe (2024). Polynomial chaos approximation (https://www.mathworks.com/matlabcentral/fileexchange/51171-polynomial-chaos-approximation), MATLAB Central File Exchange. Recuperado .
Compatibilidad con la versión de MATLAB
Compatibilidad con las plataformas
Windows macOS LinuxCategorías
- MATLAB > Mathematics > Elementary Math > Polynomials >
Etiquetas
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Descubra Live Editor
Cree scripts con código, salida y texto formateado en un documento ejecutable.
polynomial_chaos/
| Versión | Publicado | Notas de la versión | |
|---|---|---|---|
| 1.0.0.0 |