Feedback Interconnection of Passive Systems
This example illustrates the properties of a feedback interconnection of passive systems.
Feedback Interconnection of Passive Systems
Consider an interconnection of two subsystems and in feedback. The interconnected system maps the input to the output .
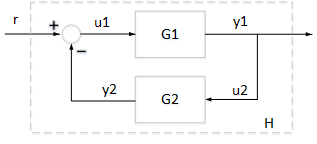
If both systems and are passive, then the interconnected system is guaranteed to be passive. Take for example
Both systems are passive as confirmed by
G1 = tf([1,1,1],[1,1,4]); isPassive(G1)
ans = logical
1
G2 = tf([1,2],[1,5]); isPassive(G2)
ans = logical
1
The interconnected system is therefore passive.
H = feedback(G1,G2); isPassive(H)
ans = logical
1
This is confirmed by verifying that the Nyquist plot of is positive real.
nyquist(H)

Passivity Indices for Feedback Interconnection
There is a relationship between the passivity indices of and and the passivity indices of the interconnected system . Let and denote the input passivity indices for and , and let and denote the output passivity indices. If all these indices are positive, then the input passivity index and the output passivity index for the feedback interconnection satisfy
In other words, we can infer some minimum level of input and output passivity for the closed-loop system from the input and output passivity indices of and . For details, see the paper by Zhu, F. and Xia, M and Antsaklis, P.J., "Passivity analysis and passivation of feedback systems using passivity indices," American Control Conference , 2014, pp. 1833-1838. Verify the lower bound for the input passivity index .
% Input passivity index for G1 nu1 = getPassiveIndex(G1,'input'); % Output passivity index for G2 rho2 = getPassiveIndex(G2,'output'); % Input passivity index for H nu = getPassiveIndex(H,'input')
nu = 0.1293
% Lower bound
nu1*rho2/(nu1+rho2)ans = 7.1402e-11
Similarly, verify the lower bound for the output passivity index of .
% Output passivity index for G1 rho1 = getPassiveIndex(G1,'output'); % Input passivity index for G2 nu2 = getPassiveIndex(G2,'input'); % Output passivity index for H rho = getPassiveIndex(H,'output')
rho = 0.4441
% Lower bound
rho1+nu2ans = 0.4000