Continuous-Time Transfer Function Estimation
This example shows how to use the Discrete Transfer Function Estimator block to estimate the magnitude and phase response of a continuous-time analog filter.
Example Model
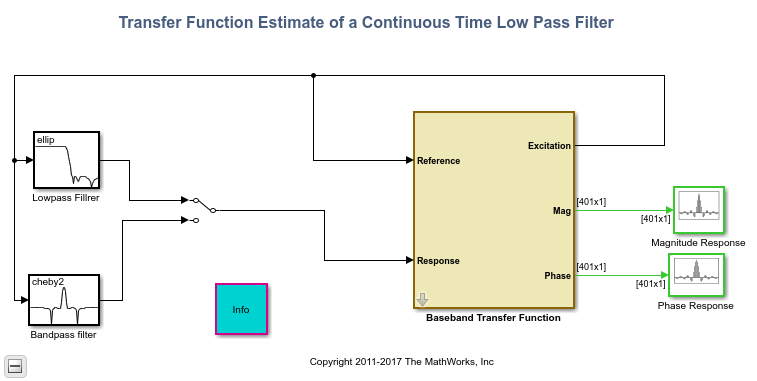

Exploring the Example
This example estimates the magnitude and phase response of two analog filters:
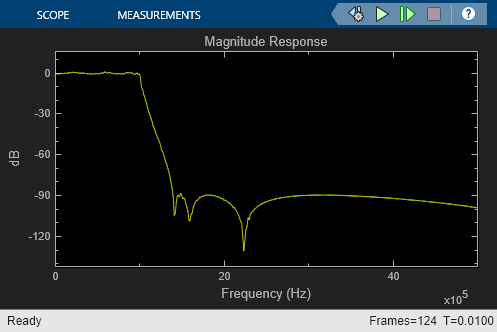
a. A lowpass, eighth-order elliptical filter with a passband edge frequency of 1 MHz.
b. A bandpass, eighth-order Chebyshev II filter with lower and upper stopband edge frequencies of 2 MHz and 3 MHz, respectively.
You can use the manual switch block to toggle between the two filters while the model is running.
You can specify the following on the dialog of the Baseband Transfer Function block: the alias-free signal bandwidth (BW), the FFT length used in transfer estimation, and the number of spectral averages used to smooth the estimate.
The excitation input is a random signal with uniform distribution. We feed the excitation through the filters under test. We pass both excitation and filtered signals through anti-alias analog filters with bandwidth BW Hz, and then we then transform them to discrete-time signals using Zero-Order Hold blocks with a sampling frequency of 2.56*BW Hz. The discrete excitation and output signals are fed to the Discrete Transfer Estimator block. The phase response is computed using a Phase Extractor block. We use array plot scopes to visualize the estimated filter magnitude and phase response.