Esta página se ha traducido mediante traducción automática. Haga clic aquí para ver la última versión en inglés.

Realización de una optimización multiobjetivo mediante el algoritmo genético

Abrir script

Este ejemplo muestra cómo realizar una optimización multiobjetivo utilizando la función de algoritmo genético multiobjetivo gamultiobj en Global Optimization Toolbox.

Problema de optimización multiobjetivo simple

gamultiobj se puede utilizar para resolver problemas de optimización multiobjetivo en varias variables. Aquí queremos minimizar dos objetivos, cada uno con una variable de decisión.

   min F(x) = [objective1(x); objective2(x)]
    x
   where, objective1(x) = (x+2)^2 - 10, and
          objective2(x) = (x-2)^2 + 20
% Plot two objective functions on the same axis
x = -10:0.5:10;
f1 = (x+2).^2 - 10;
f2 = (x-2).^2 + 20;
plot(x,f1);
hold on;
plot(x,f2,'r');
grid on;
title('Plot of objectives ''(x+2)^2 - 10'' and ''(x-2)^2 + 20''');

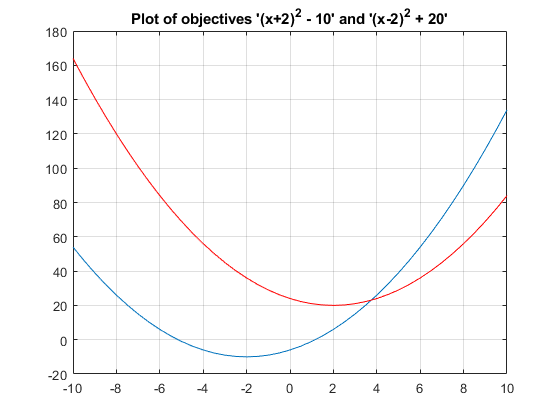
Los dos objetivos tienen sus mínimos en x = -2 y x = +2 respectivamente. Sin embargo, en un problema multiobjetivo, x = -2, x = 2 y cualquier solución en el rango -2 <= x <= 2 son igualmente óptimas. No existe una única solución para este problema multiobjetivo. El objetivo del algoritmo genético multiobjetivo es encontrar un conjunto de soluciones en ese rango (idealmente con una buena dispersión). El conjunto de soluciones también se conoce como frente de Pareto. Todas las soluciones en el frente de Pareto son óptimas.

Codificación de la función de aptitud

Creamos un archivo MATLAB® llamado simple_multiobjective.m:

   function y = simple_multiobjective(x)
   y(1) = (x+2)^2 - 10;
   y(2) = (x-2)^2 + 20;

El solucionador del algoritmo genético asume que la función de aptitud tomará una entrada x, donde x es un vector de fila con tantos elementos como el número de variables en el problema. La función de aptitud calcula el valor de cada función objetivo y devuelve estos valores en una única salida vectorial y.

Minimizar empleando gamultiobj

Para utilizar la función gamultiobj, necesitamos proporcionar al menos dos argumentos de entrada, una función de aptitud y el número de variables en el problema. Los dos primeros argumentos de salida devueltos por gamultiobj son X, los puntos en el frente de Pareto, y FVAL, los valores de la función objetivo en los valores X. Un tercer argumento de salida, exitFlag, le indica el motivo por el cual gamultiobj se detuvo. Un cuarto argumento, OUTPUT, contiene información sobre el rendimiento del solucionador. gamultiobj también puede devolver un quinto argumento, POPULATION, que contiene la población cuando finalizó gamultiobj y un sexto argumento, SCORE, que contiene los valores de función de todos los objetivos para POPULATION cuando finalizó gamultiobj.

FitnessFunction = @simple_multiobjective;
numberOfVariables = 1;
[x,fval] = gamultiobj(FitnessFunction,numberOfVariables);

gamultiobj stopped because it exceeded options.MaxGenerations.

La X devuelta por el solucionador es una matriz en la que cada fila es el punto en el frente de Pareto para las funciones objetivo. FVAL es una matriz en la que cada fila contiene el valor de las funciones objetivo evaluadas en el punto correspondiente en X.

size(x)
size(fval)

ans =

    18     1


ans =

    18     2

Problema de optimización multiobjetivo restringido

gamultiobj puede manejar problemas de optimización con desigualdad lineal, igualdad y restricciones de límites simples. Aquí queremos agregar restricciones de límites a un problema multiobjetivo simple resuelto previamente.

   min F(x) = [objective1(x); objective2(x)]
    x
   subject to  -1.5 <= x <= 0 (bound constraints)
   where, objective1(x) = (x+2)^2 - 10, and
          objective2(x) = (x-2)^2 + 20

gamultiobj acepta restricciones de desigualdad lineales en la forma A*x <= b y restricciones de igualdad lineales en la forma Aeq*x = beq y restricciones de límite en la forma lb <= x <= ub. Pasamos A y Aeq como matrices y b, beq, lb y ub como vectores. Como no tenemos restricciones lineales en este ejemplo, pasamos [] para esas entradas.

A = []; b = [];
Aeq = []; beq = [];
lb = -1.5;
ub = 0;
x = gamultiobj(FitnessFunction,numberOfVariables,A,b,Aeq,beq,lb,ub);

gamultiobj stopped because it exceeded options.MaxGenerations.

Todas las soluciones en X (cada fila) satisfarán todas las restricciones lineales y de límites dentro de la tolerancia especificada en options.ConstraintTolerance. Sin embargo, si utiliza su propia función de cruce o mutación, asegúrese de que los nuevos individuos sean factibles con respecto a las restricciones de límites lineales y simples.

Añadir visualización

gamultiobj puede aceptar una o más funciones de representación a través del argumento de opciones. Esta función es útil para visualizar el rendimiento del solucionador en tiempo de ejecución. Las funciones de representación se pueden seleccionar utilizando optimoptions .

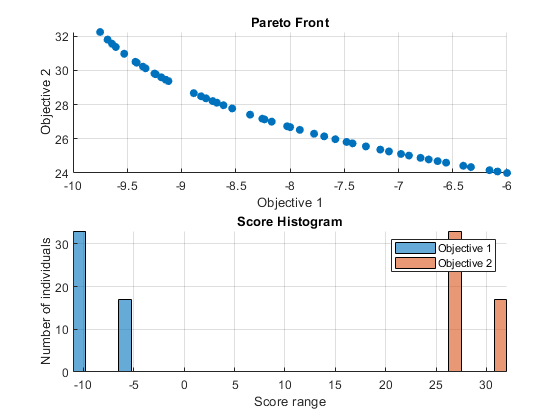
Aquí usamos optimoptions para seleccionar dos funciones de gráfico. La primera función de representación es gaplotpareto, que traza el frente de Pareto (limitado a tres objetivos) en cada generación. La segunda función de gráfico es gaplotscorediversity, que traza la diversidad de puntuaciones para cada objetivo. Las opciones se pasan como último argumento al solucionador.

options = optimoptions(@gamultiobj,'PlotFcn',{@gaplotpareto,@gaplotscorediversity});
gamultiobj(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub,options);

gamultiobj stopped because it exceeded options.MaxGenerations.

Vectorización de la función de aptitud

Consideremos nuevamente las funciones de aptitud anteriores:

   objective1(x) = (x+2)^2 - 10, and
   objective2(x) = (x-2)^2 + 20

De forma predeterminada, el solucionador gamultiobj solo pasa un punto a la vez a la función de aptitud. Sin embargo, si la función de aptitud se vectoriza para aceptar un conjunto de puntos y devuelve un conjunto de valores de función, puede acelerar su solución.

Por ejemplo, si el solucionador necesita evaluar cinco puntos en una llamada a esta función de aptitud, entonces llamará a la función con una matriz de tamaño 5 por 1, es decir, 5 filas y 1 columna (recuerde que 1 es el número de variables).

Crea un archivo MATLAB llamado vectorized_multiobjective.m:

   function scores = vectorized_multiobjective(pop)
     popSize = size(pop,1); % Population size
     numObj = 2;  % Number of objectives
     % initialize scores
     scores = zeros(popSize, numObj);
     % Compute first objective
     scores(:,1) = (pop + 2).^2 - 10;
     % Compute second objective
     scores(:,2) = (pop - 2).^2 + 20;

Esta versión vectorizada de la función de aptitud toma una matriz pop con un número arbitrario de puntos, las filas de pop, y devuelve una matriz de tamaño populationSize por numberOfObjectives.

Necesitamos especificar que la función de aptitud se vectoriza usando las opciones creadas usando optimoptions. Las opciones se pasan como noveno argumento.

FitnessFunction = @(x) vectorized_multiobjective(x);
options = optimoptions(@gamultiobj,'UseVectorized',true);
gamultiobj(FitnessFunction,numberOfVariables,[],[],[],[],lb,ub,options);

gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.

Consulte también

Temas