globe
Frame for 3-D map display on axesm-based map
Classification
Spherical
Identifier
globe
Graticule
This map display is based on a coordinate transformation and is not a true map projection.
Meridians, parallels, and displayed map data appear in a 3-D view that depends on the
view and camera settings of the axesm-based map. Change the view
interactively or by using the view function. Change the camera
settings using the camposm, camtargm, and camupm functions.
Features
In the 3-D sense, globe is true in scale, equal-area, conformal, minimum
error, and equidistant everywhere.
While globe has none of the distortions inherent in planar
projections, it cannot be displayed without distortion or in its entirety. In order to
render the globe in a figure window, either a perspective or orthographic transformation
must be applied, both of which necessarily involve setting a viewpoint, hiding the back
side and distortions of shape, scale, and angles.
Parallels
The globe requires no standard parallels.
Remarks
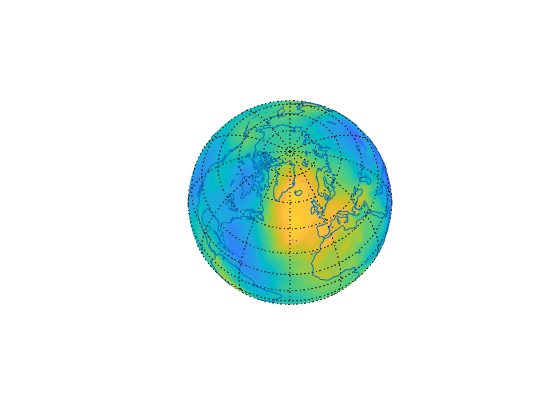
The globe display allows you to visualize terrain relief or other
data for an entire planet viewed from space. Its underlying transformation maps
latitude, longitude, and elevation to a 3-D Cartesian frame. The
globe display is different from other transformations because
it can render relative relief of elevations above, below, or on a sphere.
When displayed, the globe looks like an orthographic azimuthal projection, provided
that the Projection property of the
axesm-based map is set to 'orthographic'.
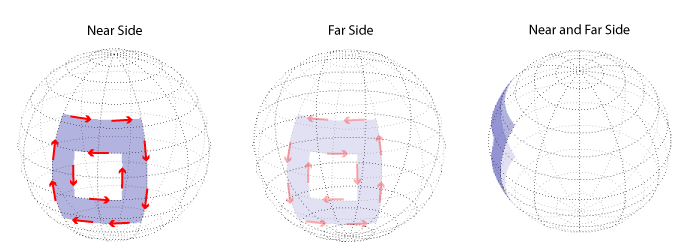
Examples
Version History
Introduced before R2006a