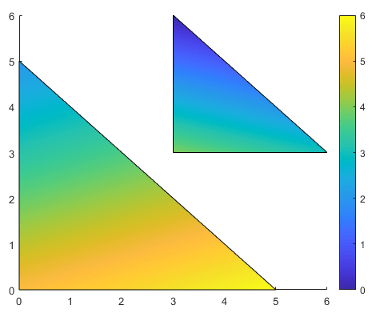Cómo se relacionan los datos de parches a un mapa de colores
Cuando crea gráficas que utilizan objetos de Patch, puede controlar el esquema de colores general llamando a la función colormap. También puede controlar la relación entre el mapa de colores y su parche:
asignando colores específicos a las caras
asignando colores específicos a los vértices que rodean cada cara
El modo en que controla dichas relaciones depende de cómo especifique sus parches: como las coordenadas -x, -y y -z o como datos vértice-cara.
Relación del mapa de colores del arreglo de las coordenadas -x, -y y -z
Si crea un objeto de Patch con un arreglo de coordenadas -x, -y y -z, la propiedad de CData del objeto de Patch contiene un arreglo de indexación C. El arreglo controla la relación entre el mapa de colores y su parche. Para asignar colores a las caras, especifique C como un arreglo con las siguientes características:
Ces un arreglo n por 1, donde n es el número de caras.El valor de
C(i)controla el color de la carai.
A continuación se muestra un ejemplo de C y su relación con el mapa de colores y las tres caras. El valor de C(i) controla el color de la cara definida por los vértices (X(i,:), Y(i,:)).
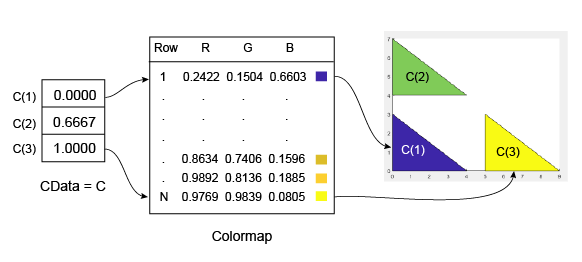
El valor más pequeño de C es 0. Se asigna a la primera fila del mapa de colores. El valor más grande de C es 1 y se asigna a la última fila del mapa de colores. Los valores intermedios de C se asignan de forma lineal a las filas intermedias del mapa de colores. En este caso, C(2) se asigna al color ubicado a dos tercios del comienzo del mapa de colores. Este código crea el objeto Patch que se describe en la ilustración anterior.
X = [0 0 5; 0 0 5; 4 4 9]; Y = [0 4 0; 3 7 3; 0 4 0]; C = [0; .6667; 1]; p = patch(X,Y,C); colorbar
Para asignar colores a los vértices, especifique C como un arreglo con las siguientes características:
Ces un arreglo m por n, donde m es el número de vértices por cara y n es el número de caras.El valor de
C(i,j)controla el color del vérticeide la caraj.
A continuación se muestra un ejemplo de C y su relación con el mapa de colores y los seis vértices. El valor de C(i,j) controla el color de los vértices (X(i,j), Y(i,j)).
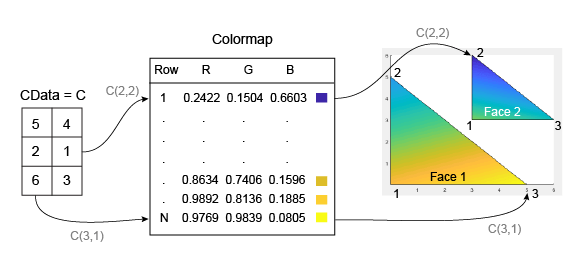
Al igual que con las caras del parche, MATLAB® ajusta los valores de C al número de filas del mapa de colores. En este caso, el valor más pequeño es C(2,2)=1 y se asigna a la primera fila del mapa de colores. El valor más grande es C(3,1)=6 y se asigna a la última fila del mapa de colores.
Este código crea el objeto Patch que se describe en la ilustración anterior. La propiedad FaceColor se establece en 'interp' para hacer que los colores de los vértices se mezclen en cada cara.
clf X = [0 3; 0 3; 5 6]; Y = [0 3; 5 6; 0 3]; C = [5 4; 2 0; 6 3]; p = patch(X,Y,C,'FaceColor','interp'); colorbar
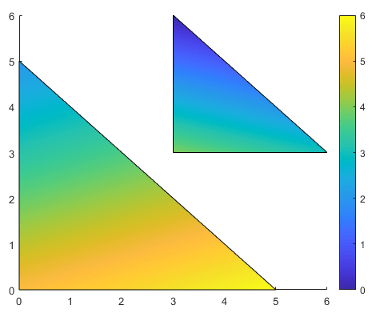
Relación del mapa de colores con los datos vértice-cara
Si crea parche de con datos vértice-cara, la propiedad de FaceVertexCData del objeto de Patch contiene un arreglo de indexación C. El arreglo controla la relación entre el mapa de colores y su parche.
Para asignar colores a las caras, especifique C como un arreglo con las siguientes características:
Ces un arreglo n por 1, donde n es el número de caras.El valor de
C(i)controla el color de la carai.
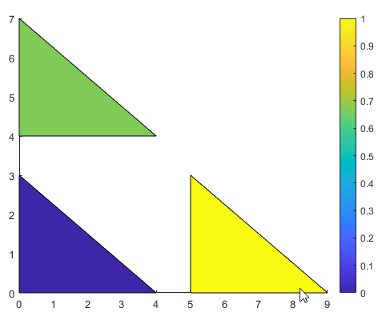
A continuación se muestra un ejemplo de C y su relación con el mapa de colores y las tres caras.
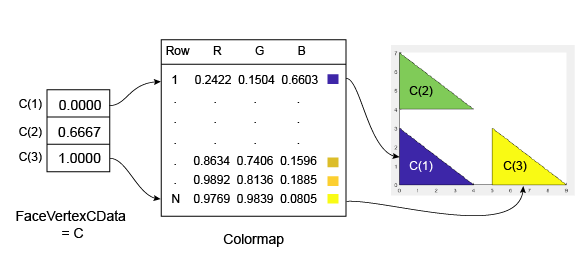
El valor más pequeño en C es 0 y se asigna a la primera fila del mapa de colores. El valor más grande en C es 1 y se asigna al último valor del mapa de colores. Los valores intermedios de C se asignan de forma lineal a las filas intermedias del mapa de colores. En este caso, C(2) se asigna al color ubicado a dos tercios del final del mapa de colores.
Este código crea el objeto Patch que se describe en la ilustración anterior. La propiedad FaceColor se establece en 'flat' para mostrar los colores del mapa de colores en lugar del color predeterminado, que es negro.
clf vertices = [0 0; 0 3; 4 0; 0 4; 0 7; 4 4; 5 0; 5 3; 9 0]; faces = [1 2 3; 4 5 6; 7 8 9]; C = [0; 0.6667; 1]; p = patch('Faces',faces,'Vertices',vertices,'FaceVertexCData',C); p.FaceColor = 'flat'; colorbar

Para asignar colores a los vértices, especifique la propiedad FaceVertexCData del objeto de Patch como un arreglo C con las siguientes características:
Ces un arreglo n por 1, donde n es el número de vértices.El valor de
C(i)controla el color del vérticei.
A continuación se muestra un ejemplo de C y su relación con el mapa de colores y los seis vértices.
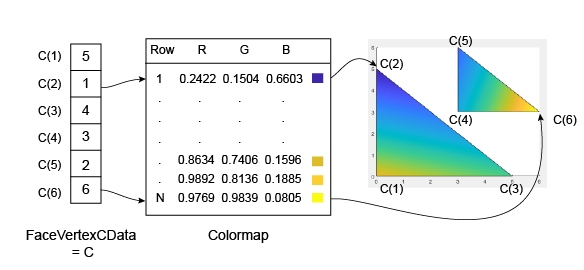
Al igual que con las caras del parche, MATLAB ajusta los valores de C al número de filas del mapa de colores. En este caso, el valor más pequeño es C(2)=1 y se asigna a la primera fila del mapa de colores. El valor más grande es C(6)=6 y se asigna a la última fila del mapa de colores.
Este código crea el objeto Patch que se describe en la ilustración anterior. La propiedad FaceColor se establece en 'interp' para que los colores del vértice se mezclen en cada cara.
clf vertices = [0 0; 0 5; 5 0; 3 3; 3 6; 6 3]; faces = [1 2 3; 4 5 6]; C = [5; 1; 4; 3; 2; 6]; p = patch('Faces',faces,'Vertices',vertices,'FaceVertexCData',C); p.FaceColor = 'interp'; colorbar