La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

Matemáticas de precisión simple

Abrir script en vivo

Este ejemplo muestra cómo ejecutar aritmética y álgebra lineal con datos de precisión simple. También muestra cómo los resultados se calculan de forma adecuada en precisión simple o doble precisión, dependiendo de la entrada.

Crear datos de doble precisión

Creemos primero algunos datos, que de forma predeterminada son de doble precisión.

Ad = [1 2 0; 2 5 -1; 4 10 -1]

Ad = 3×3

     1     2     0
     2     5    -1
     4    10    -1

Convertir a precisión simple

Se pueden convertir datos a precisión simple con la función single.

A = single(Ad); % or A = cast(Ad,'single');

Crear ceros y unos de precisión simple

También se pueden crear ceros y unos de precisión simple con sus respectivas funciones.

n = 1000;
Z = zeros(n,1,'single');
O = ones(n,1,'single');

Examinemos las variables en el espacio de trabajo.

whos A Ad O Z n

  Name         Size            Bytes  Class     Attributes

  A            3x3                36  single              
  Ad           3x3                72  double              
  O         1000x1              4000  single              
  Z         1000x1              4000  single              
  n            1x1                 8  double

Vemos que algunas de las variables son de tipo single y que la variable A (la versión en precisión simple de Ad) necesita para su almacenamiento la mitad de la cantidad de bytes de memoria porque los valores simples requieren únicamente cuatro bytes (32 bits), mientras que los valores dobles requieren 8 bytes (64 bits).

Aritmética y álgebra lineal

Se puede ejecutar aritmética estándar y álgebra lineal con valores simples.

B = A'    % Matrix Transpose

B = 3x3 single matrix

     1     2     4
     2     5    10
     0    -1    -1

whos B

  Name      Size            Bytes  Class     Attributes

  B         3x3                36  single

Vemos que el resultado de esta operación, B, es un valor simple.

C = A * B % Matrix multiplication

C = 3x3 single matrix

     5    12    24
    12    30    59
    24    59   117

C = A .* B % Elementwise arithmetic

C = 3x3 single matrix

     1     4     0
     4    25   -10
     0   -10     1

X = inv(A) % Matrix inverse

X = 3x3 single matrix

     5     2    -2
    -2    -1     1
     0    -2     1

I = inv(A) * A % Confirm result is identity matrix

I = 3x3 single matrix

     1     0     0
     0     1     0
     0     0     1

I = A \ A  % Better way to do matrix division than inv

I = 3x3 single matrix

     1     0     0
     0     1     0
     0     0     1

E = eig(A) % Eigenvalues

E = 3x1 single column vector

    3.7321
    0.2679
    1.0000

F = fft(A(:,1)) % FFT

F = 3x1 single column vector

   7.0000 + 0.0000i
  -2.0000 + 1.7321i
  -2.0000 - 1.7321i

S = svd(A) % Singular value decomposition

S = 3x1 single column vector

   12.3171
    0.5149
    0.1577

P = round(poly(A)) % The characteristic polynomial of a matrix

P = 1x4 single row vector

     1    -5     5    -1

R = roots(P) % Roots of a polynomial

R = 3x1 single column vector

    3.7321
    1.0000
    0.2679

Q = conv(P,P) % Convolve two vectors

Q = 1x7 single row vector

     1   -10    35   -52    35   -10     1

R = conv(P,Q)

R = 1x10 single row vector

     1   -15    90  -278   480  -480   278   -90    15    -1

stem(R); % Plot the result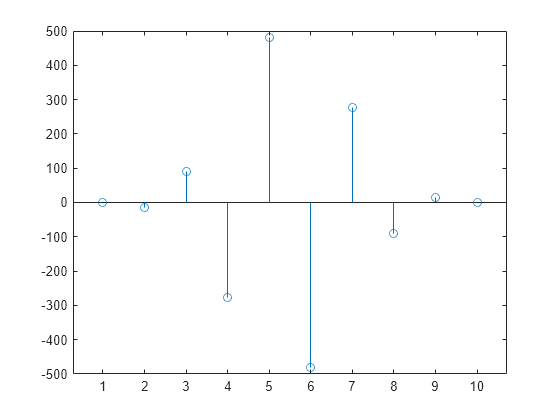

Figure contains an axes object. The axes object contains an object of type stem.

Un programa que trabaja tanto en precisión simple como en doble precisión

Veamos ahora una función para calcular suficientes términos en la sucesión de Fibonacci para que la relación sea menor que el épsilon de la máquina correcto (eps) para tipos de datos simples o dobles.

% How many terms needed to get single precision results?
fibodemo('single')

ans = 19

% How many terms needed to get double precision results?
fibodemo('double')

ans = 41

% Now let's look at the working code.
type fibodemo

function nterms = fibodemo(dtype)
%FIBODEMO Used by SINGLEMATH demo.
% Calculate number of terms in Fibonacci sequence.

% Copyright 1984-2014 The MathWorks, Inc.

fcurrent = ones(dtype);
fnext = fcurrent;
goldenMean = (ones(dtype)+sqrt(5))/2;
tol = eps(goldenMean);
nterms = 2;
while abs(fnext/fcurrent - goldenMean) >= tol
   nterms = nterms + 1;
   temp  = fnext;
   fnext = fnext + fcurrent;
   fcurrent = temp;
end

Observe que se inicializan varias de las variables, fcurrent, fnext y goldenMean, con valores que dependen del tipo de datos de entrada, y que la tolerancia tol depende también de ese tipo. La precisión simple requiere que se calculen menos términos que en el cálculo equivalente de doble precisión.