Elevator
This example models an elevator system comprising a car with passengers, a counterweight, a hoist cable, and a compensating cable. The motor drives a top pulley. A PID controller senses the car's velocity and adjusts the motor torque to achieve the velocity command. In this scenario, the elevator starts at rest, moves upward at 1 m/s, stops, then moves downward at -1 m/s, and stops again. Sensors measure the car's height, velocity, and acceleration, as well as the motor's torque, power, and energy.
The building height is 144 meters, and the elevator well depth is 5 meters. The car mass is 1000 kg, while the passenger mass is 375 kg. The counterweight mass is 1500 kg. The hoist cable runs from the top of the car, over the top pulley, to the top of the counterweight. The compensating cable runs from the bottom of the car, under the bottom pulley, to the bottom of the counterweight. The hoist and compensating cables have matching linear densities of 11.1 kg/m. If the combined weight of the car and passengers equals the counterweight, minimal energy is required to move the car. In this scenario, since the car and passengers weigh less than the counterweight, the motor absorbs power while the car travels upwards. The motor exerts power while the car travels downwards.
Model

The model uses four cable blocks to represent the hoist and compensating cables on both sides of the pulleys. As shown in the dialog box of Hoist Cable 1, the cable blocks account for variable rest length, linear density, and gravity. The L input signal to each block represents the cable length, which is the sum of the cable's rest length and stretch. The velocity at the cable's B and F ports represents the material velocity at instantaneous contact points. The cable's rest length changes as the contact points travel to new material points on the cables. Consequently, the cable stiffness and mass change as the rest length changes. The cable block models half of the cable mass at port B and half of the cable mass at port F.

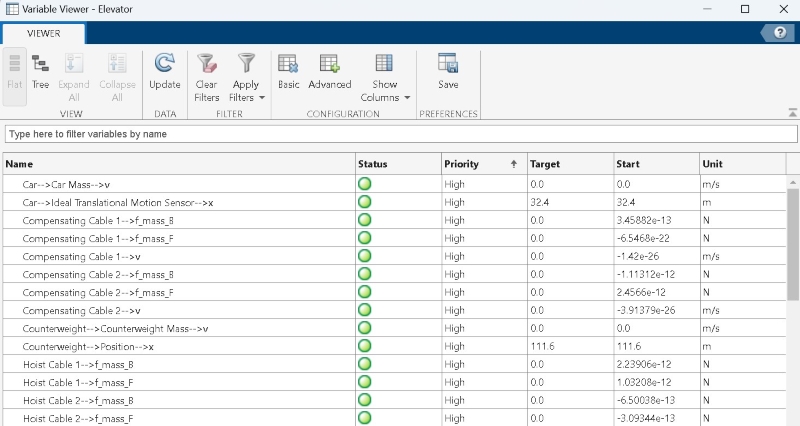
To initialize the system at rest, the car and counterweight masses have high priority target velocities of 0 m/s. The cables have none priority targets for stretch and high priority targets of 0 N for the force of mass acceleration at both ports. The force of mass acceleration at each cable port equals half the cable mass multiplied by the port acceleration. Setting this force to 0 allows the Simscape solver to balance the cable stiffness forces with the gravity forces. The PID controller provides an initial torque command to the motor to offset the gravity imbalance of the car and counterweight. The Variable Viewer, shown below, indicates all of the high priority targets for Simscape blocks in the model.
Car Subsystem
The Car subsystem models the mass and acceleration force of the car and passengers.

Gravity Force Subsystem
The Gravity Force subsystem models the downward force of gravity acting on the car and passengers.
Simulation Results from Scopes
In this model, positive translational velocity indicates upward movement. Positive rotational velocity indicates counterclockwise rotation. Gravity acts downward, exerting negative forces on the passengers, car, counterweight, and cables.
Since the counterweight is heavier than the car and passengers, the motor must apply negative (counterclockwise) torque to keep the car stationary. To start moving the car upward, the motor applies a burst of positive (clockwise) torque. The motor then switches to applying negative torque to maintain a constant upward velocity of the car. As the car moves, damping effects on the car and counterweight reduce the motor torque needed to maintain the commanded speed. When slowing the car to a stop, the motor applies negative torque. To accelerate the car downward, the motor applies another burst of negative torque. A final burst of positive torque slows the car to a stop again.
Due to the weight difference between the car and counterweight, the motor absorbs power while moving the car upward and exerts power while moving the car downward. Since the car ends the scenario 10 meters lower than where it started, the motor has a net positive energy expenditure.

