Prediction Polynomial
This example shows how to obtain the prediction polynomial from an autocorrelation sequence. The example also shows that the resulting prediction polynomial has an inverse that produces a stable all-pole filter. You can use the all-pole filter to filter a wide-sense stationary white noise sequence to produce a wide-sense stationary autoregressive process.
Create an autocorrelation sequence defined by
k = 0:2; rk = (24/5)*2.^(-k)-(27/10)*3.^(-k);
Use ac2poly to obtain the prediction polynomial of order 2, which is
A = ac2poly(rk);
Examine the pole-zero plot of the FIR filter to see that the zeros are inside the unit circle.
zplane(A,1) grid
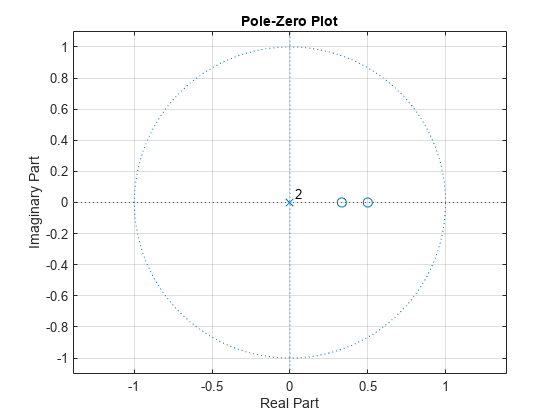
The inverse all-pole filter is stable with poles inside the unit circle.
zplane(1,A)
grid
title('Poles and Zeros')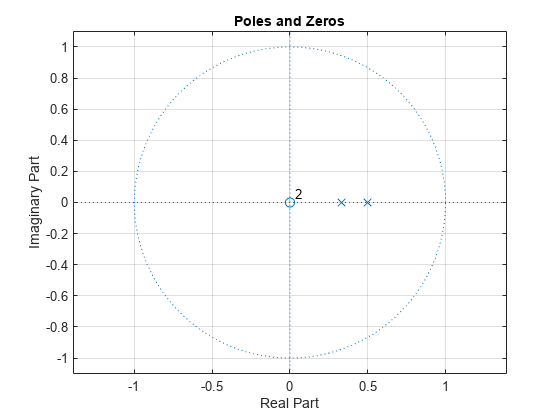
Use the all-pole filter to produce a realization of a wide-sense stationary AR(2) process from a white-noise sequence. Set the random number generator to the default settings for reproducible results.
rng default
x = randn(1000,1);
y = filter(1,A,x);Compute the sample autocorrelation of the AR(2) realization and show that the sample autocorrelation is close to the true autocorrelation.
[xc,lags] = xcorr(y,2,'biased');
[xc(3:end) rk']ans = 3×2
2.2401 2.1000
1.6419 1.5000
0.9980 0.9000