Modelar y depurar un motor de CC en Stateflow
Este ejemplo muestra el modelo de un motor de CC de imanes permanentes. Tanto la lógica del modo como la dinámica del motor de CC se modelizan mediante Stateflow®.
El gráfico de estados del motor de CC consta de dos superestados: powerOn (encendido) y powerOff (apagado). Si el motor está encendido, puede estar en uno de dos subestados: arriba o abajo, lo que indica la dirección del movimiento.
Nota: Se trata de un modelo simplista de un motor de CC. Puede crear modelos de motores de CC más sofisticados con Simscape™, que amplía Simulink® con herramientas para modelización y simulación de sistemas físicos multidominio, como aquellos con componentes mecánicos, hidráulicos y eléctricos.
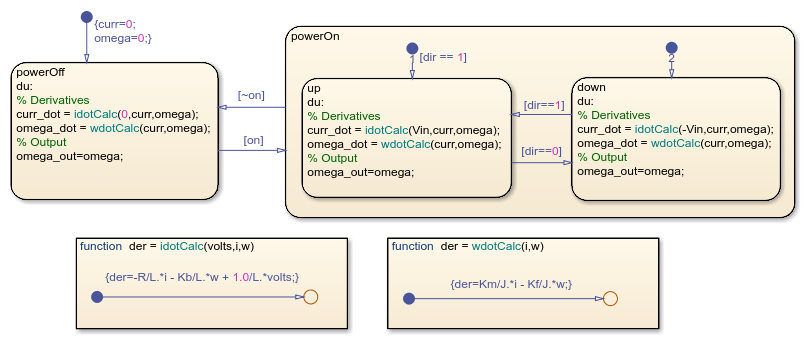
La dinámica del motor se define directamente en el gráfico de estados mediante funciones gráficas y cambia según el estado del motor. Por ejemplo, cuando el motor está en estado powerOff, la tensión aplicada es igual a cero. Cuando el motor está en estado powerOn, la tensión aplicada es positiva o negativa, según la dirección del motor.
Para repasar, las ecuaciones diferenciales que definen un motor de CC de imanes permanentes son las siguientes:
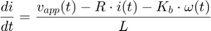

donde

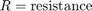


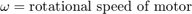
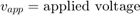
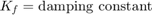
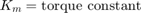
Activar una salida de estado activo
Para activar la monitorización de la salida de estado activo, primero seleccione el estado powerOn. Después, en la pestaña Simulation, haga clic en Log Child Activity.
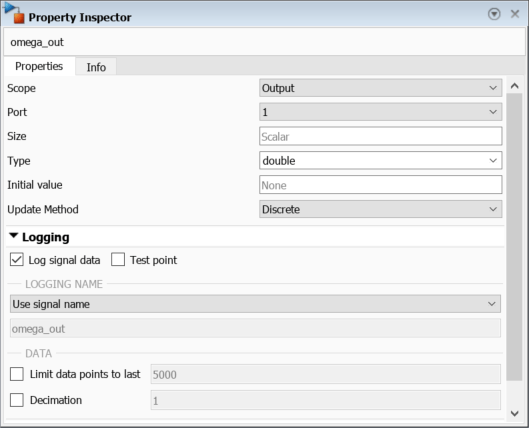
Ejecute la simulación.
En la sección Review Results de la pestaña Simulation, el botón Data Inspector está resaltado, lo que significa que hay una señal registrada disponible para su visualización. Haga clic en el botón Data Inspector para ver los datos de la simulación.
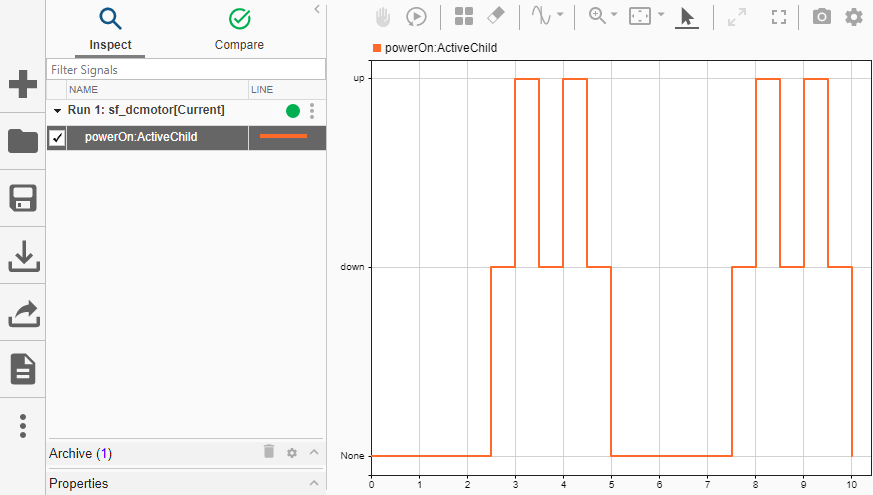
En esta gráfica, los datos de color naranja muestran qué estado secundario de powerOn está activo. La gráfica muestra que los estados secundarios alternan entre down y up.
Depurar con una salida de estado activo
Las salidas de estado activo también pueden ayudar a depurar gráficos de Stateflow. Para esta parte del ejemplo, introduzca un error en el gráfico de Stateflow eliminando la transición desde up hasta down. Elimine la transición predeterminada desde down y elimine la condición de la transición predeterminada hasta up.
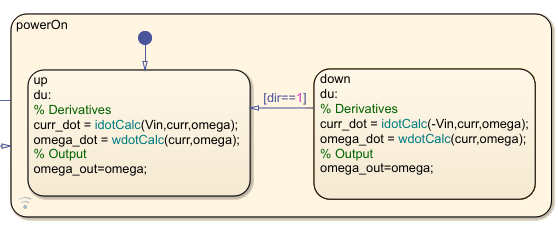
Ejecute la simulación.
De nuevo, el botón Data Inspector muestra que se han registrado datos nuevos. Abra Data Inspector para observar la señal.

En esta gráfica, puede observar que el único estado secundario de powerOn que se activa es up.