Random Subspace Classification
This example shows how to use a random subspace ensemble to increase the accuracy of classification. It also shows how to use cross validation to determine good parameters for both the weak learner template and the ensemble.
Load the data
Load the ionosphere data. This data has 351 binary responses to 34 predictors.
load ionosphere;
[N,D] = size(X)N = 351
D = 34
resp = unique(Y)
resp = 2×1 cell
{'b'}
{'g'}
Choose the number of nearest neighbors
Find a good choice for k, the number of nearest neighbors in the classifier, by cross validation. Choose the number of neighbors approximately evenly spaced on a logarithmic scale.
rng(8000,'twister') % for reproducibility K = round(logspace(0,log10(N),10)); % number of neighbors cvloss = zeros(numel(K),1); for k=1:numel(K) knn = fitcknn(X,Y,... 'NumNeighbors',K(k),'CrossVal','On'); cvloss(k) = kfoldLoss(knn); end figure; % Plot the accuracy versus k semilogx(K,cvloss); xlabel('Number of nearest neighbors'); ylabel('10 fold classification error'); title('KNN classification');
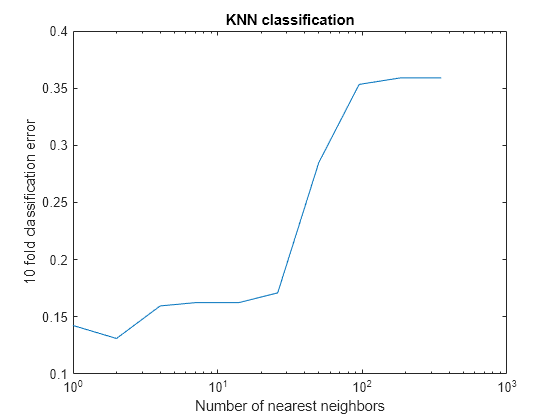
The lowest cross-validation error occurs for k = 2.
Create the ensembles
Create ensembles for 2-nearest neighbor classification with various numbers of dimensions, and examine the cross-validated loss of the resulting ensembles.
This step takes a long time. To keep track of the progress, print a message as each dimension finishes.
NPredToSample = round(linspace(1,D,10)); % linear spacing of dimensions cvloss = zeros(numel(NPredToSample),1); learner = templateKNN('NumNeighbors',2); for npred=1:numel(NPredToSample) subspace = fitcensemble(X,Y,'Method','Subspace','Learners',learner, ... 'NPredToSample',NPredToSample(npred),'CrossVal','On'); cvloss(npred) = kfoldLoss(subspace); fprintf('Random Subspace %i done.\n',npred); end
Random Subspace 1 done. Random Subspace 2 done. Random Subspace 3 done. Random Subspace 4 done. Random Subspace 5 done. Random Subspace 6 done. Random Subspace 7 done. Random Subspace 8 done. Random Subspace 9 done. Random Subspace 10 done.
figure; % plot the accuracy versus dimension plot(NPredToSample,cvloss); xlabel('Number of predictors selected at random'); ylabel('10 fold classification error'); title('KNN classification with Random Subspace');
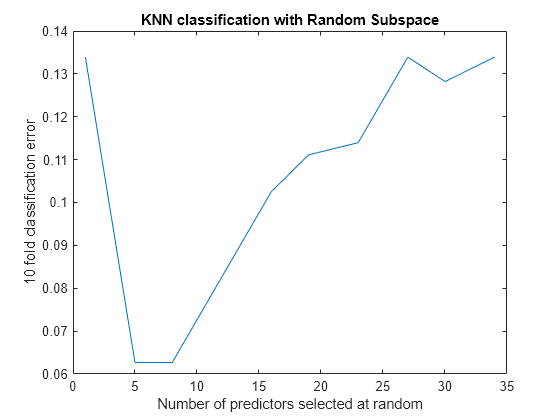
The ensembles that use five and eight predictors per learner have the lowest cross-validated error. The error rate for these ensembles is about 0.06, while the other ensembles have cross-validated error rates that are approximately 0.1 or more.
Find a good ensemble size
Find the smallest number of learners in the ensemble that still give good classification.
ens = fitcensemble(X,Y,'Method','Subspace','Learners',learner, ... 'NPredToSample',5,'CrossVal','on'); figure; % Plot the accuracy versus number in ensemble plot(kfoldLoss(ens,'Mode','Cumulative')) xlabel('Number of learners in ensemble'); ylabel('10 fold classification error'); title('KNN classification with Random Subspace');
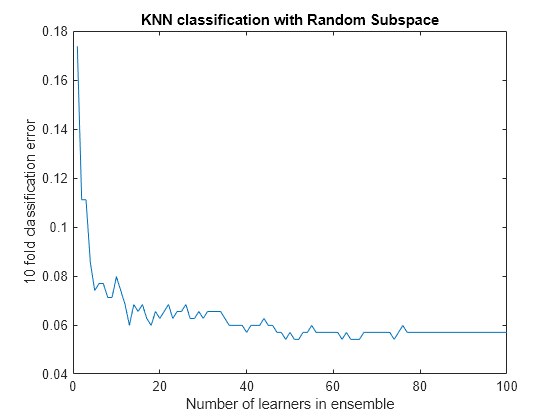
There seems to be no advantage in an ensemble with more than 50 or so learners. It is possible that 25 learners gives good predictions.
Create a final ensemble
Construct a final ensemble with 50 learners. Compact the ensemble and see if the compacted version saves an appreciable amount of memory.
ens = fitcensemble(X,Y,'Method','Subspace','NumLearningCycles',50,... 'Learners',learner,'NPredToSample',5); cens = compact(ens); s1 = whos('ens'); s2 = whos('cens'); [s1.bytes s2.bytes] % si.bytes = size in bytes
ans = 1×2
1760904 1529460
The compact ensemble is about 10% smaller than the full ensemble. Both give the same predictions.
See Also
fitcknn | fitcensemble | kfoldLoss | templateKNN | compact