Límites de confianza y predicción
Sobre los límites de confianza y predicción
El software de la Curve Fitting Toolbox™ le permite calcular límites de confianza para los coeficientes ajustados y límites de predicción para las nuevas observaciones o para la función ajustada. Además, en el caso de los límites de predicción, puede calcular límites simultáneos (que tienen en cuenta todos los valores predictores) o no simultáneos (que solo tienen en cuenta valores predictores individuales). Los límites de confianza de coeficientes se presentan de forma numérica. Los límites de predicción se muestran gráficamente, además de estar disponibles de forma numérica.
A continuación, se resumen los límites de confianza y predicción que existen.
Tipos de límites de confianza y predicción
Tipo de intervalo | Descripción |
|---|---|
Coeficientes ajustados | Límites de confianza para los coeficientes ajustados |
Nueva observación | Límites de predicción para una nueva observación (valor de respuesta) |
Nueva función | Límites de predicción para el valor de una nueva función |
Nota
A menudo, los límites de predicción se describen como límites de confianza porque se calcula un intervalo de confianza para una respuesta prevista.
Los límites de confianza y predicción definen los valores inferior y superior del intervalo asociado, así como la anchura de este. La anchura del intervalo indica su grado de incertidumbre sobre los coeficientes ajustados, la observación prevista o el ajuste previsto. Por ejemplo, un intervalo muy ancho para los coeficientes ajustados puede indicar que debería usar más datos para hacer un ajuste antes de poder afirmar algo con certeza sobre los coeficientes.
Los límites se definen con el nivel de certidumbre que especifique. A menudo, el nivel de certidumbre es de 95%, pero puede tomar cualquier valor como 90%, 99%, 99,9%, etc. Por ejemplo, es posible que quiera arriesgarse a fallar en la predicción de una nueva observación con una probabilidad del 5%. En ese caso, calcularía un intervalo de predicción del 95%. Este intervalo indica que tiene una probabilidad del 95% de que la nueva observación se encuentre entre los límites de predicción inferior y superior.
Límites de confianza en los coeficientes
Los límites de confianza para los coeficientes ajustados vienen dados por
donde b son los coeficientes producidos por el ajuste, t depende del nivel de confianza y se calcula usando la inversa de la función de distribución acumulada t de Student, y S es un vector de los elementos diagonales de la matriz de covarianzas estimada de las estimaciones de los coeficientes, (XTX)–1s2. En un ajuste lineal, X es la matriz de diseño; en el caso de un ajuste no lineal, X es el jacobiano de los valores ajustados respecto a los coeficientes. XT es la traspuesta de X y s2 es el error cuadrático medio.
Los límites de confianza se muestran en el panel Results de la app Curve Fitter con el siguiente formato.
p1 = 1.275 (1.113, 1.437)
El valor ajustado del coeficiente p1 es 1,275, el límite inferior es 1,113, el límite superior es 1,437 y la anchura del intervalo es 0,324. De forma predeterminada, el nivel de confianza para los límites es del 95%.
Puede calcular intervalos de confianza en la línea de comandos con la función confint.
Límites de predicción en los ajustes
Como ya se ha mencionado, puede calcular los límites de predicción para la curva ajustada. La predicción se basa en un ajuste existente de los datos. Además, los límites pueden ser simultáneos (y medir la confianza para todos los valores predictores) o no simultáneos (y medir la confianza solo para un único valor predictor predeterminado). Si está prediciendo una nueva observación, los límites no simultáneos miden la confianza en que la nueva observación quede dentro del intervalo dado un único valor predictor. Los límites simultáneos miden la confianza en que la nueva observación quede dentro del intervalo con independencia del valor predictor.
| Tipo de límites | Observación | Funcional |
|---|---|---|
| Simultáneo |
|
|
| No simultáneo |
|
|
Donde:
s2 es el error cuadrático medio;
t depende del nivel de confianza y se calcula usando la inversa de la función de distribución acumulada t de Student;
f depende del nivel de confianza y se calcula usando la inversa de la función de distribución acumulada F;
S es la matriz de covarianzas de las estimaciones de coeficientes, (XTX)–1s2;
x es un vector fila del jacobiano o la matriz de diseño evaluado según un valor predictor concreto.
Puede mostrar gráficamente los límites de predicción mediante la app Curve Fitter. La app Curve Fitter le permite mostrar límites de predicción no simultáneos para nuevas observaciones. En la pestaña Curve Fitter, en la sección Visualization, seleccione un nivel de certidumbre de la lista Prediction Bounds. Puede cambiar este nivel por cualquier otro valor seleccionando Custom de la lista.
Puede mostrar cualquier tipo de límites de predicción numéricos en la línea de comandos con la función predint.
Para comprender las cantidades asociadas con cada tipo de intervalo de predicción, recuerde que los datos, el ajuste y los valores residuales están relacionados mediante la fórmula
datos = ajuste + valores residuales
donde los términos ajuste y valores residuales son estimaciones de los términos de la fórmula
datos = modelo + error aleatorio
Supongamos que prevé realizar una nueva observación del valor predictor xn+1. Llame a la nueva observación yn+1(xn+1) y al error asociado εn+1. Entonces,
yn+1(xn+1) = f(xn+1) + εn+1
donde f(xn+1) es la función verdadera pero desconocida que desea estimar en xn+1. Los límites de predicción no simultáneos proporcionan los valores probables de la nueva observación o de la función estimada.
Si en lugar de ello desea que el valor probable de la nueva observación esté asociado con cualquier valor predictor, la ecuación anterior se convierte en
yn+1(x) = f(x) + ε
Los límites de predicción simultáneos proporcionan los valores probables de esta nueva observación o de la función estimada.
A continuación, se resumen los tipos de límites de predicción.
Tipos de límites de predicción
Tipo de límite | Simultáneo o no simultáneo | Ecuación asociada |
|---|---|---|
Observación | No simultáneo | yn+1(xn+1) |
Simultáneos | yn+1(x) para todo x | |
Función | No simultáneo | f(xn+1) |
Simultáneos | f(x) para todo x |
A continuación, se muestran los límites de predicción simultáneos y no simultáneos para una nueva observación y la función ajustada. Cada gráfica contiene tres curvas: el ajuste, el límite de confianza inferior y el límite de confianza superior. El ajuste es una exponencial de un solo término de los datos generados y los límites reflejan un nivel de confianza del 95%. Tenga en cuenta que los intervalos asociados con una nueva observación son mayores que los intervalos de funciones ajustados debido a la incertidumbre adicional al predecir un nuevo valor de respuesta (la curva más los errores aleatorios).

Calcular intervalos de predicción desde la línea de comandos
Calcule y represente intervalos de predicción funcionales y de las observaciones para ajustar datos ruidosos.
Genere datos ruidosos mediante una tendencia exponencial.
x = (0:0.2:5)'; y = 2*exp(-0.2*x) + 0.5*randn(size(x));
Ajuste una curva a los datos mediante una exponencial de un solo término.
fitresult = fit(x,y,'exp1');Calcule intervalos de predicción funcionales y de las observaciones del 95%, tanto simultáneos como no simultáneos. Los límites no simultáneos son para elementos individuales de x; los límites simultáneos son para todos los elementos de x.
p11 = predint(fitresult,x,0.95,'observation','off'); p12 = predint(fitresult,x,0.95,'observation','on'); p21 = predint(fitresult,x,0.95,'functional','off'); p22 = predint(fitresult,x,0.95,'functional','on');
Represente los datos, el ajuste y los intervalos de predicción. Los límites de las observaciones son mayores que los funcionales porque miden la incertidumbre al predecir la curva ajustada más la variación aleatoria de la nueva observación.
subplot(2,2,1) plot(fitresult,x,y), hold on, plot(x,p11,'m--'), xlim([0 5]), ylim([-1 5]) title('Nonsimultaneous Observation Bounds','FontSize',9) legend off subplot(2,2,2) plot(fitresult,x,y), hold on, plot(x,p12,'m--'), xlim([0 5]), ylim([-1 5]) title('Simultaneous Observation Bounds','FontSize',9) legend off subplot(2,2,3) plot(fitresult,x,y), hold on, plot(x,p21,'m--'), xlim([0 5]), ylim([-1 5]) title('Nonsimultaneous Functional Bounds','FontSize',9) legend off subplot(2,2,4) plot(fitresult,x,y), hold on, plot(x,p22,'m--'), xlim([0 5]), ylim([-1 5]) title('Simultaneous Functional Bounds','FontSize',9) legend({'Data','Fitted curve', 'Prediction intervals'},... 'FontSize',8,'Location','northeast')
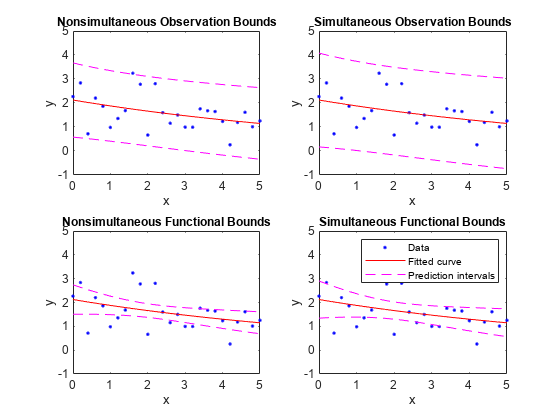
Calcular límites de predicción con la app Curve Fitter
Cargue el conjunto de datos census.
load censusLas variables cdate y pop contienen datos sobre la fecha y la población cuando se realizó el censo.
Abra la app Curve Fitter.
curveFitter
En la app, seleccione las variables de datos para el ajuste. En la sección Data de la pestaña Curve Fitter, haga clic en Select Data. En el cuadro de diálogo Select Fitting Data, seleccione cdate como el valor X data y pop como el valor Y data.

La app representa los puntos de datos a medida que selecciona las variables.

La gráfica muestra los datos del censo y el ajuste lineal para los datos.
Represente los límites de predicción del 95% para el ajuste. En la sección Visualization de la pestaña Curve Fitter, seleccione 95% para Prediction Bounds.
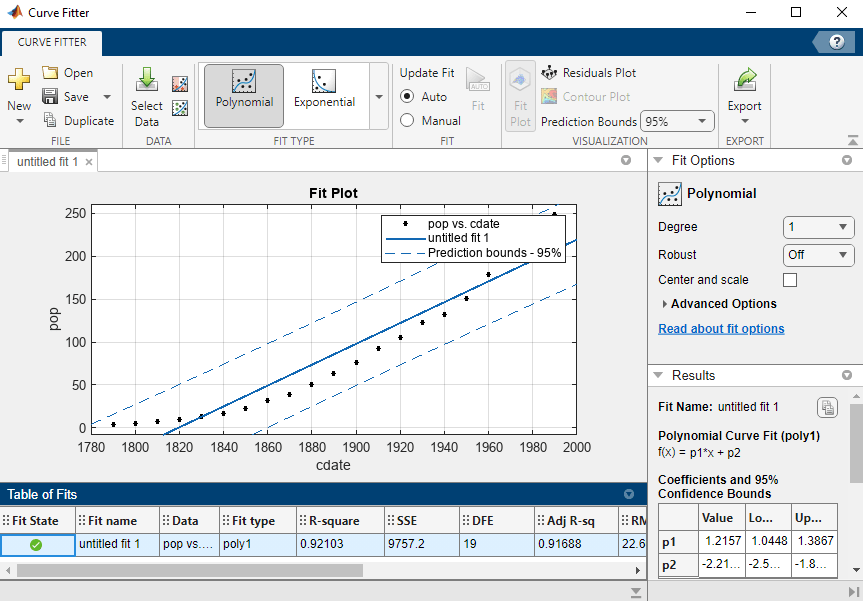
Ahora la gráfica muestra los intervalos de predicción del 95%, además de los datos del censo y el ajuste lineal.
Para representar los límites de predicción del 60% para el ajuste, debe especificar un nivel de confianza personalizado. En la sección Visualization de la pestaña Curve Fitter, seleccione Custom para Prediction Bounds. En el cuadro de diálogo Set Prediction Bounds, introduzca 60 en el cuadro Confidence level (%) y haga clic en OK.


Ahora la gráfica muestra los intervalos de predicción del 60%, además de los datos del censo y el ajuste lineal. Juntas, las dos gráficas muestran que los intervalos de predicción del 60% se encuentran más cerca del ajuste lineal que los intervalos de predicción del 95%.