fnxtr

Extrapolar un spline

Sintaxis

pp = fnxtr(f,order)

pp = fnxtr(f)

Descripción

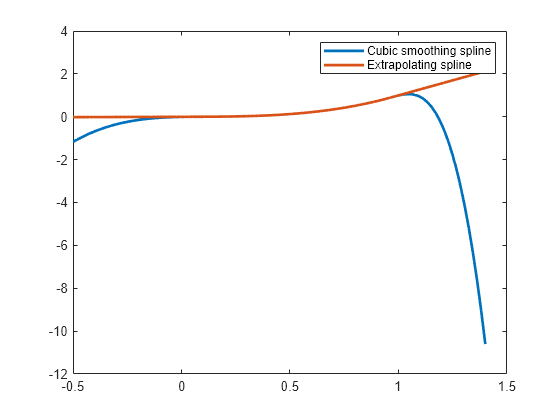
pp = fnxtr(f,order) devuelve un spline de orden order que extrapola el spline f. pp es igual a f en su intervalo básico, pero pp es un polinomio del orden dado fuera de ese intervalo. pp satisface al menos order condiciones de suavidad en los extremos del intervalo básico de f, es decir, en los nuevos saltos. Resulta más útil utilizar un valor positivo de order que sea inferior al orden de f.

pp = fnxtr(f) utiliza un orden de extrapolación igual a 2. Es equivalente a fnxtr(f,2).

Ejemplos

Extrapolar spline cúbico de suavizado

Cree un spline cúbico de suavizado en el intervalo de la unidad.

x = rand(1,21);
spline = csaps(x,x.^3); 

Cree un spline de extrapolación de orden 2.

order = 2;
extrSpline = fnxtr(spline,order);

Represente el spline original junto con el spline de extrapolación.

fnplt(spline,[-.5 1.4])
hold on
fnplt(extrSpline,[-.5 1.4])
legend('Cubic smoothing spline','Extrapolating spline')
hold off

Extrapolar un B-spline bivariado

Cree y represente un B-spline bivariado.

spline = spmak({0:3,0:4},1);
fnplt(spline)

Cree un spline de extrapolación. Para extrapolar solo en la primera variable, especifique un entero negativo como el orden de extrapolación en la segunda variable.

order = [3,-1];
extrSpline = fnxtr(spline,order);
fnplt(extrSpline)

Argumentos de entrada

f — Spline que se desea extrapolar

estructura

Spline que se desea extrapolar, especificado como estructura. f debe ser un spline en formato B-form, BBform o ppform.

Tipos de datos: struct

order — Orden del spline de extrapolación

valor entero | vector de enteros

Orden del spline de extrapolación, especificado como entero o vector de enteros.

Si order es cero, el spline de extrapolación describe el mismo spline como fn2fm(f,'B-'), pero está en formato ppform y tiene un intervalo básico más grande.

Si order es al menos tan grande como el orden de f, el spline de extrapolación es el mismo spline que gn2fm(f,'pp'), pero utiliza dos tramos más y tiene un intervalo básico más grande.

Si f es m-variado, order puede ser un vector con m elementos, donde order(i) es el orden utilizado para extrapolar en la i-ésima variable. Para excluir la i-ésima variable y que no se utilice en la extrapolación, especifique order(i) como entero negativo.

Ejemplo: 1

Argumentos de salida

pp — Spline en formato ppform

estructura de spline

Spline en formato ppform, devuelto como estructura con los siguientes campos.

Form — Forma del spline

pp

Forma del spline, devuelta como pp. pp indica que el spline tiene forma polinomial por tramos.

Breaks — Ubicaciones de los nudos del spline

vector | arreglo de celdas

Posiciones de los nudos del spline, devueltas como un vector o un arreglo de celdas de vectores en el caso de datos multivariantes. Los vectores contienen elementos estrictamente crecientes que representan el inicio y el fin de cada uno de los intervalos en los que se definen los tramos polinomiales.

Coefs — Coeficientes de los polinomios

matriz | arreglo

Coeficientes de los polinomios para cada tramo, devueltos como una matriz o como un arreglo en el caso de datos multivariantes.

Pieces — Número de tramos polinomiales

escalar | vector

Número de tramos polinomiales que describen el spline, devuelto como un escalar o como un vector de números de tramos de cada variable en el caso de datos multivariantes.

Order — Orden de los polinomios

escalar | vector

Orden de la función polinómica que describe cada tramo polinomial del spline, devuelta como un escalar o como un vector que contiene el orden de cada variable en el caso de datos multivariantes.

Dim — Dimensionalidad

escalar

Dimensionalidad de la función de destino, devuelta como un escalar.

Historial de versiones

Introducido en R2006a

Consulte también

ppmak | spmak | fn2fm