La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

trainAutoencoder

Entrenar un codificador automático

Sintaxis

autoenc = trainAutoencoder(X)

autoenc = trainAutoencoder(X,hiddenSize)

autoenc = trainAutoencoder(___,Name,Value)

Descripción

autoenc = trainAutoencoder(X) devuelve un codificador automático, autoenc, entrenado usando los datos de entrenamiento de X.

autoenc = trainAutoencoder(X,hiddenSize) devuelve un codificador automático autoenc, con el tamaño de la representación oculta de hiddenSize.

autoenc = trainAutoencoder(___,Name,Value) devuelve un codificador automático autoenc, para cualquiera de los argumentos de entrada anteriores con opciones adicionales especificadas por uno o varios argumentos de par Name,Value.

Por ejemplo, puede especificar la proporción de escasez o el número máximo de iteraciones de entrenamiento.

Ejemplos

Entrenar un codificador automático disperso

Cargue los datos de muestra.

X = abalone_dataset;

X es una matriz de 8 por 4177 que define ocho atributos para 4177 conchas de abulón diferentes: sexo (M, F e I [para crías]), longitud, diámetro, altura, peso total, peso desconchado, peso de las vísceras y peso de la concha. Para obtener más información sobre el conjunto de datos, escriba help abalone_dataset en la línea de comandos.

Entrene un codificador automático disperso con la configuración predeterminada.

autoenc = trainAutoencoder(X);

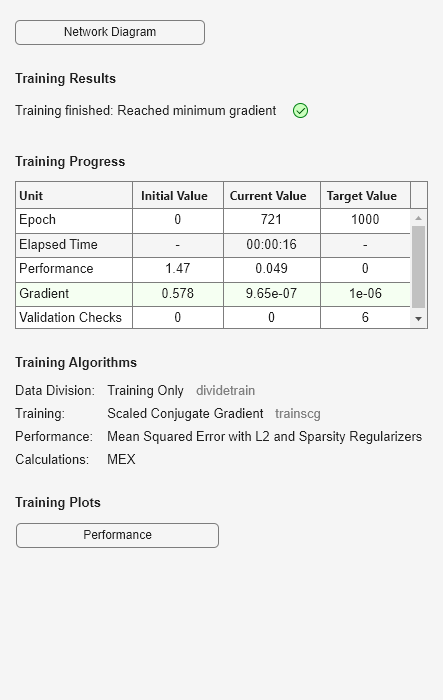
Reconstruya los datos de anillos de conchas de abulón utilizando el codificador automático entrenado.

XReconstructed = predict(autoenc,X);

Calcule el error de reconstrucción cuadrático medio.

mseError = mse(X-XReconstructed)

mseError = 0.0167

Entrenar un codificador automático con opciones especificadas

Cargue los datos de muestra.

X = abalone_dataset;

X es una matriz de 8 por 4177 que define ocho atributos para 4177 conchas de abulón diferentes: sexo (M, F e I [para crías]), longitud, diámetro, altura, peso total, peso desconchado, peso de las vísceras y peso de la concha. Para obtener más información sobre el conjunto de datos, escriba help abalone_dataset en la línea de comandos.

Entrene un codificador automático disperso con tamaño oculto 4, 400 épocas máximas y función de transferencia lineal para el decodificador.

autoenc = trainAutoencoder(X,4,'MaxEpochs',400,...
'DecoderTransferFunction','purelin');

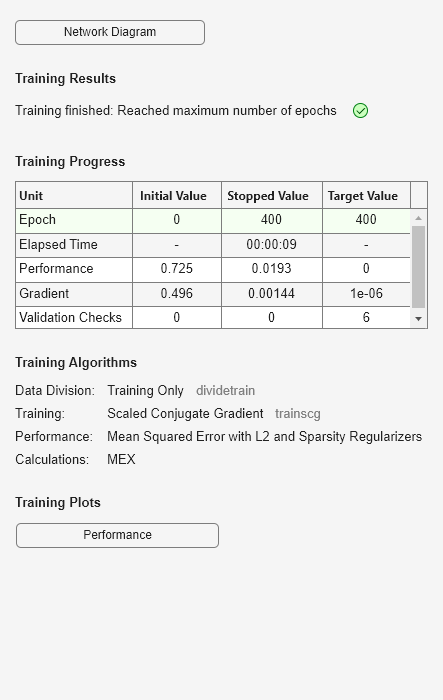
Reconstruya los datos de anillos de conchas de abulón utilizando el codificador automático entrenado.

XReconstructed = predict(autoenc,X);

Calcule el error de reconstrucción cuadrático medio.

mseError = mse(X-XReconstructed)

mseError = 0.0044

Reconstruir observaciones con un codificador automático disperso

Genere los datos de entrenamiento.

rng(0,'twister'); % For reproducibility
n = 1000;
r = linspace(-10,10,n)';
x = 1 + r*5e-2 + sin(r)./r + 0.2*randn(n,1);

Entrene el codificador automático con los datos de entrenamiento.

hiddenSize = 25;
autoenc = trainAutoencoder(x',hiddenSize,...
        'EncoderTransferFunction','satlin',...
        'DecoderTransferFunction','purelin',...
        'L2WeightRegularization',0.01,...
        'SparsityRegularization',4,...
        'SparsityProportion',0.10);

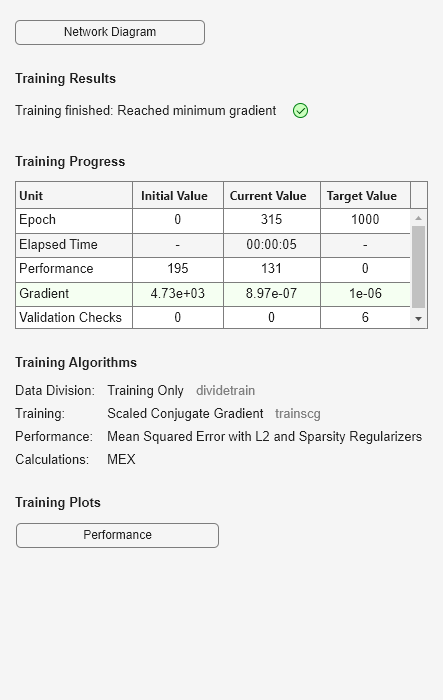
Genere los datos de prueba.

n = 1000;
r = sort(-10 + 20*rand(n,1));
xtest = 1 + r*5e-2 + sin(r)./r + 0.4*randn(n,1);

Prediga los datos de prueba con el codificador automático entrenado, autoenc.

xReconstructed = predict(autoenc,xtest');

Represente los datos de prueba reales y las predicciones.

figure;
plot(xtest,'r.');
hold on
plot(xReconstructed,'go');

Reconstruir imágenes de dígitos manuscritos con el codificador automático disperso

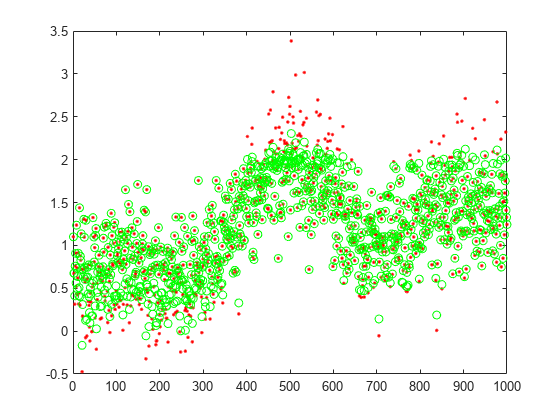
Cargue los datos de entrenamiento.

XTrain = digitTrainCellArrayData;

Los datos de entrenamiento son un arreglo de 1 por 5000 celdas, donde cada celda contiene una matriz de 28 por 28 que representa una imagen sintética de un dígito manuscrito.

Entrene un codificador automático con una capa oculta que contenga 25 neuronas.

hiddenSize = 25;
autoenc = trainAutoencoder(XTrain,hiddenSize,...
        'L2WeightRegularization',0.004,...
        'SparsityRegularization',4,...
        'SparsityProportion',0.15);

Cargue los datos de prueba.

XTest = digitTestCellArrayData;

Los datos de prueba son un arreglo de 1 por 5000 celdas, donde cada celda contiene una matriz de 28 por 28 que representa una imagen sintética de un dígito manuscrito.

Reconstruya los datos de imagen de prueba con el codificador automático entrenado, autoenc.

xReconstructed = predict(autoenc,XTest);

Visualice los datos de prueba reales.

figure;
for i = 1:20
    subplot(4,5,i);
    imshow(XTest{i});
end

Visualice los datos de prueba reconstruidos.

figure;
for i = 1:20
    subplot(4,5,i);
    imshow(xReconstructed{i});
end

Argumentos de entrada

X — Datos de entrenamiento

matriz | arreglo de celdas de datos de imagen

Datos de entrenamiento, especificados como una matriz de muestras de entrenamiento o un arreglo de celdas de datos de imagen. Si X es una matriz, entonces cada columna contiene una sola muestra. Si X es un arreglo de celdas de datos de imagen, entonces los datos de cada celda deben tener el mismo número de dimensiones. Los datos de imagen pueden ser datos de intensidad de píxeles para imágenes en escala de grises, en cuyo caso cada celda contiene una matriz de m por n. De forma alternativa, los datos de imagen pueden ser datos RGB, en cuyo caso cada celda contiene una matriz de m por n por 3.

Tipos de datos: single | double | cell

hiddenSize — Tamaño de la representación oculta del codificador automático

10 (predeterminado) | valor entero positivo

Tamaño de la representación oculta del codificador automático, especificado como un valor entero positivo. Este número es el número de neuronas de la capa oculta.

Tipos de datos: single | double

Argumentos de par nombre-valor

Especifique pares de argumentos opcionales como Name1=Value1,...,NameN=ValueN, donde Name es el nombre del argumento y Value es el valor correspondiente. Los argumentos de nombre-valor deben aparecer después de otros argumentos. Sin embargo, el orden de los pares no importa.

En las versiones anteriores a la R2021a, utilice comas para separar cada nombre y valor, y encierre Name entre comillas.

Ejemplo: 'EncoderTransferFunction','satlin','L2WeightRegularization',0.05 especifica la función de transferencia para el codificador como la función de transferencia lineal saturante positiva y la regularización del peso L2 como 0,05.

EncoderTransferFunction — Función de transferencia del codificador

'logsig' (predeterminado) | 'satlin'

Función de transferencia del codificador, especificada como el par separado por comas que consta de 'EncoderTransferFunction' y uno de los siguientes:

Opción de la función de transferencia	Definición
'logsig'	Función sigmoide logística $$f\left(z\right)=\frac{1}{1+e^{-z}}$$
'satlin'	Función de transferencia lineal saturada positiva $$f\left(z\right)=\{\begin{array}{cc}0,& \text{if }z\le 0\\ z\text{,}& \text{if }0<z<1\\ 1,& \text{if}z\ge 1\end{array}$$

Ejemplo: 'EncoderTransferFunction','satlin'

DecoderTransferFunction — Función de transferencia del decodificador

'logsig' (predeterminado) | 'satlin' | 'purelin'

Función de transferencia del decodificador, especificada como el par separado por comas que consta de 'DecoderTransferFunction' y uno de los siguientes:

Opción de la función de transferencia	Definición
'logsig'	Función sigmoide logística $$f\left(z\right)=\frac{1}{1+e^{-z}}$$
'satlin'	Función de transferencia lineal saturada positiva $$f\left(z\right)=\{\begin{array}{cc}0,& \text{if }z\le 0\\ z\text{,}& \text{if }0<z<1\\ 1,& \text{if}z\ge 1\end{array}$$
'purelin'	Función de transferencia lineal $$f\left(z\right)=z$$

Ejemplo: 'DecoderTransferFunction','purelin'

MaxEpochs — Número máximo de épocas de entrenamiento

1000 (predeterminado) | valor entero positivo

Número máximo de épocas de entrenamiento o iteraciones, especificado como el par separado por comas que consta de 'MaxEpochs' y un entero positivo.

Ejemplo: 'MaxEpochs',1200

L2WeightRegularization — El coeficiente para el regularizador de peso L₂

0.001 (predeterminado) | un valor escalar positivo

El coeficiente para el regularizador de peso L₂ en la función de coste (LossFunction), especificado como el par separado por comas que consta de 'L2WeightRegularization' y un valor escalar positivo.

Ejemplo: 'L2WeightRegularization',0.05

LossFunction — Función de pérdida que se desea usar para el entrenamiento

'msesparse' (predeterminado)

Función de pérdida que se desea usar para el entrenamiento, especificada como el par separado por comas que consta de 'LossFunction' y 'msesparse'. Corresponde a la función de error cuadrático medio ajustada para entrenar un codificador automático disperso de la siguiente manera:

$$E=\underset{\text{mean squared error}}{\underbrace{\frac{1}{N}{\displaystyle \sum _{n=1}^N{\displaystyle \sum _{k=1}^K{\left(x_{kn}-{\widehat{x}}_{kn}\right)}^2}}}}+\lambda *\underset{\begin{array}{c}{L}_2\\ \text{regularization}\end{array}}{\underbrace{{\Omega }_{weights}}}+\beta *\underset{\begin{array}{c}\text{sparsity}\\ \text{regularization}\end{array}}{\underbrace{{\Omega }_{sparsity}}},$$

donde λ es el coeficiente del término de regularización L₂ y β es el coeficiente del término de regularización de escasez. Puede especificar los valores de λ y β utilizando los argumentos de par nombre-valor L2WeightRegularization y SparsityRegularization, respectivamente, mientras entrena un codificador automático.

ShowProgressWindow — Indicador para mostrar la ventana de entrenamiento

true (predeterminado) | false

Indicador para mostrar la ventana de entrenamiento, especificado como el par separado por comas que consta de 'ShowProgressWindow' y true o false.

Ejemplo: 'ShowProgressWindow',false

SparsityProportion — Proporción deseada de ejemplos de entrenamiento a los que reacciona una neurona

0.05 (predeterminado) | valor escalar positivo que oscila entre 0 y 1

Proporción deseada de ejemplos de entrenamiento a los que reacciona una neurona, especificada como el par separado por comas que consta de 'SparsityProportion' y un valor escalar positivo. La proporción de escasez es un parámetro del regularizador de escasez. Controla la escasez de la salida desde la capa oculta. Un valor bajo de SparsityProportion generalmente lleva a que cada neurona de la capa oculta se "especialice" al proporcionar solo una salida alta para una pequeña cantidad de ejemplos de entrenamiento. Por lo tanto, una proporción de escasez baja fomenta un mayor grado de escasez. Consulte Sparse Autoencoders.

Ejemplo: 'SparsityProportion',0.01 equivale a decir que cada neurona de la capa oculta debe tener una salida media de 0,1 en los ejemplos de entrenamiento.

SparsityRegularization — Coeficiente que controla el impacto del regularizador de escasez

1 (predeterminado) | un valor escalar positivo

Coeficiente que controla el impacto del regularizador de escasez en la función de coste, especificado como el par separado por comas que consta de 'SparsityRegularization' y un valor escalar positivo.

Ejemplo: 'SparsityRegularization',1.6

TrainingAlgorithm — El algoritmo que se desea utilizar para entrenar el codificador automático

'trainscg' (predeterminado)

El algoritmo que se desea utilizar para entrenar el codificador automático, especificado como el par separado por comas que consta de 'TrainingAlgorithm' y 'trainscg'. Significa gradiente descendente conjugado escalado [1].

ScaleData — Indicador para volver a escalar los datos de entrada

true (predeterminado) | false

Indicador para volver a escalar los datos de entrada, especificado como el par separado por comas que consta de 'ScaleData' y true o false.

Los codificadores automáticos intentan replicar la entrada en la salida. Para que sea posible, el rango de los datos de entrada debe coincidir con el rango de la función de transferencia del decodificador. trainAutoencoder escala automáticamente los datos de entrenamiento para que se ajusten a este rango al entrenar un codificador automático. Si los datos se escalaron durante el entrenamiento de un codificador automático, los métodos predict, encode y decode también escalan los datos.

Ejemplo: 'ScaleData',false

UseGPU — Indicador para usar la GPU para el entrenamiento

false (predeterminado) | true

Indicador para usar la GPU para el entrenamiento, especificado como el par separado por comas que consta de 'UseGPU' y true o false.

Ejemplo: 'UseGPU',true

Argumentos de salida

autoenc — Codificador automático entrenado

objeto Autoencoder

Codificador automático entrenado, devuelto como objeto Autoencoder. Para obtener información sobre las propiedades y los métodos de este objeto, consulte la página de clase Autoencoder.

Más acerca de

Codificadores automáticos

Un codificador automático es una red neuronal entrenada para replicar su entrada en su salida. El entrenamiento de un codificador automático no está supervisado en el sentido de que no se necesitan datos etiquetados. El proceso de entrenamiento todavía se basa en la optimización de una función de coste. La función de coste mide el error entre la entrada x y su reconstrucción en la salida $$\widehat{x}$$.

Un codificador automático está compuesto de un codificador y un decodificador. El codificador y decodificador pueden tener varias capas, pero por simplicidad considere que cada uno de ellos tiene una sola capa.

Si la entrada a un codificador automático es un vector $$x\in {ℝ}^{D_x}$$, entonces el codificador asigna el vector x a otro vector $$z\in {ℝ}^{D^{\left(1\right)}}$$ de la siguiente manera:

$$z=h^{{}^{\left(1\right)}}\left(W^{\left(1\right)}x+b^{\left(1\right)}\right),$$

donde el superíndice (1) indica la primera capa. $$h^{\left(1\right)}:{ℝ}^{D^{\left(1\right)}}\to {ℝ}^{D^{\left(1\right)}}$$ es una función de transferencia del codificador, $$W^{\left(1\right)}\in {ℝ}^{D^{\left(1\right)}\times D_{{}^x}}$$ es una matriz de peso y $$b^{\left(1\right)}\in {ℝ}^{D^{\left(1\right)}}$$ es un vector de sesgo. A continuación, el decodificador asigna la representación codificada z nuevamente a una estimación del vector de entrada original, x, de la siguiente manera:

$$\widehat{x}=h^{{}^{\left(2\right)}}\left(W^{\left(2\right)}z+b^{\left(2\right)}\right),$$

donde el superíndice (2) representa la segunda capa. $$h^{\left(2\right)}:{ℝ}^{D_x}\to {ℝ}^{D_x}$$ es la función de transferencia del decodificador, $$W^{\left(1\right)}\in {ℝ}^{D_{{}^x}\times D^{\left(1\right)}}$$ es una matriz de peso y $$b^{\left(2\right)}\in {ℝ}^{D_x}$$ es un vector de sesgo.

Codificadores automáticos dispersos

Es posible fomentar la escasez de un codificador automático añadiendo un regularizador a la función de coste [2]. Este regularizador es una función del valor medio de activación de salida de una neurona. La medida media de activación de salida de una neurona i se define como:

$${\widehat{\rho }}_i=\frac{1}{n}{\displaystyle \sum _{j=1}^n{z}_i^{\left(1\right)}\left(x_j\right)}=\frac{1}{n}{\displaystyle \sum _{j=1}^{n}h\left(w_i^{\left(1\right)T}{x}_j+b_i^{\left(1\right)}\right)},$$

donde n es el número total de ejemplos de entrenamiento. x_j es el j-ésimo ejemplo de entrenamiento, $$w_i^{\left(1\right)T}$$ es la i-ésima fila de la matriz de peso $$W^{\left(1\right)}$$ y $$b_i^{\left(1\right)}$$ es la i-ésima entrada del vector de sesgo, $$b^{\left(1\right)}$$. Se considera que una neurona está "disparándose" si su valor de activación de salida es alto. Un valor de activación de salida bajo significa que la neurona de la capa oculta se activa en respuesta a una pequeña cantidad de ejemplos de entrenamiento. Añadir un término a la función de coste que limite los valores de $${\widehat{\rho }}_i$$ para que sean bajos fomenta que el codificador automático aprenda una representación, donde cada neurona de la capa oculta se activa ante una pequeña cantidad de ejemplos de entrenamiento. Es decir, cada neurona se especializa respondiendo a alguna característica que solo está presente en un pequeño subconjunto de los ejemplos de entrenamiento.

Regularización de escasez

El regularizador de escasez intenta imponer una restricción a la escasez de la salida desde la capa oculta. Se puede fomentar la escasez añadiendo un término de regularización que tome un valor grande cuando el valor de activación medio, $${\widehat{\rho }}_i$$, de una neurona i y su valor deseado, $$\rho$$, no tienen un valor similar [2]. Uno de estos términos de regularización de escasez puede ser la divergencia de Kullback-Leibler.

$${\Omega }_{sparsity}={\displaystyle \sum _{i=1}^{D^{\left(1\right)}}KL\left(\rho \parallel {\widehat{\rho }}_i\right)}={\displaystyle \sum _{i=1}^{D^{\left(1\right)}}\rho \log \left(\frac{\rho }{{\widehat{\rho }}_i}\right)+\left(1-\rho \right)\log \left(\frac{1-\rho }{1-{\widehat{\rho }}_i}\right)}$$

La divergencia de Kullback-Leibler es una función que mide cuán diferentes son dos distribuciones. En este caso, toma el valor cero cuando $$\rho$$ y $${\widehat{\rho }}_i$$ son iguales entre sí y aumenta a medida que divergen entre sí. Minimizar la función de coste obliga a que este término sea pequeño y, por lo tanto, a que $$\rho$$ y $${\widehat{\rho }}_i$$ estén cerca el uno del otro. Puede definir el valor deseado para el valor de activación medio utilizando el argumento de par nombre-valor SparsityProportion mientras entrena un codificador automático.

Regularización L₂

Al entrenar un codificador automático disperso, es posible hacer que el regularizador de dispersión sea pequeño aumentando los valores de los pesos w^(l) y disminuyendo los valores de z⁽¹⁾ [2]. Añadir un término de regularización en los pesos de la función de coste evita que esto suceda. Este término se denomina el término de regularización L₂ y se define como:

$${\Omega }_{weights}=\frac{1}{2}{\displaystyle \sum _{l=1}^L{\displaystyle \sum _{j=1}^{n_l}{\displaystyle \sum _{i=1}^{k_l}{\left(w_{ji}^{(l)}\right)}^2}}},$$

donde L es el número de capas ocultas, n_l es el tamaño de salida de la capa l y k_l es el tamaño de entrada de la capa l. El término de regularización L₂ es la suma de los cuadrados de los elementos de las matrices de peso para cada capa.

Función de coste

La función de coste para entrenar un codificador automático disperso es una función de error cuadrático medio ajustada de la siguiente manera:

$$E=\underset{\text{mean squared error}}{\underbrace{\frac{1}{N}{\displaystyle \sum _{n=1}^N{\displaystyle \sum _{k=1}^K{\left(x_{kn}-{\widehat{x}}_{kn}\right)}^2}}}}+\lambda *\underset{\begin{array}{c}{L}_2\\ \text{regularization}\end{array}}{\underbrace{{\Omega }_{weights}}}+\beta *\underset{\begin{array}{c}\text{sparsity}\\ \text{regularization}\end{array}}{\underbrace{{\Omega }_{sparsity}}},$$

donde λ es el coeficiente del término de regularización L₂ y β es el coeficiente del término de regularización de escasez. Puede especificar los valores de λ y β utilizando los argumentos de par nombre-valor L2WeightRegularization y SparsityRegularization, respectivamente, mientras entrena un codificador automático.

Referencias

[1] Moller, M. F. “A Scaled Conjugate Gradient Algorithm for Fast Supervised Learning”, Neural Networks, Vol. 6, 1993, pp. 525–533.

[2] Olshausen, B. A. and D. J. Field. “Sparse Coding with an Overcomplete Basis Set: A Strategy Employed by V1.” Vision Research, Vol.37, 1997, pp.3311–3325.

Historial de versiones

Introducido en R2015b

Consulte también

trainSoftmaxLayer | Autoencoder | encode | stack

Temas

• Train Stacked Autoencoders for Image Classification