Deep learning usando la optimización bayesiana
En este ejemplo se muestra cómo aplicar la optimización bayesiana a deep learning y encontrar los hiperparámetros óptimos de la red, así como las opciones de entrenamiento para redes neuronales convolucionales.
Para entrenar una red neuronal profunda, debe especificar la arquitectura de la red neuronal, así como las opciones del algoritmo de entrenamiento. Seleccionar estos hiperparámetros y ajustarlos puede ser difícil y llevar tiempo. La optimización bayesiana es un algoritmo bien adaptado para optimizar hiperparámetros de modelos de clasificación y regresión. La optimización bayesiana se puede utilizar para optimizar funciones no diferenciables, discontinuas y laboriosas de evaluar. El algoritmo mantiene internamente un modelo de proceso gaussiano de la función objetivo y utiliza evaluaciones de la función objetivo para entrenar este modelo.
En este ejemplo se muestra cómo llevar a cabo las operaciones siguientes:
Descargar y preparar el conjunto de datos CIFAR-10 para el entrenamiento de la red. Este conjunto de datos es uno de los conjuntos de datos más utilizados para realizar pruebas con modelos de clasificación de imágenes.
Especificar las variables que se desea optimizar usando la optimización bayesiana. Estas variables son opciones del algoritmo de entrenamiento, así como parámetros de la arquitectura de la misma red.
Definir la función objetivo, que toma los valores de las variables de optimización como entradas, especifica la arquitectura de la red y las opciones de entrenamiento, entrena y valida la red, y guarda la red entrenada en el disco. La función objetivo se define al final de este script.
Realizar la optimización bayesiana minimizando el error de clasificación en el conjunto de validación.
Cargar la mejor red desde el disco y evaluarla en el conjunto de prueba.
Como alternativa, puede utilizar la optimización bayesiana para encontrar opciones de entrenamiento óptimas en Experiment Manager. Para obtener más información, consulte Tune Experiment Hyperparameters by Using Bayesian Optimization.
Preparar los datos
Descargue el conjunto de datos CIFAR-10 [1]. Este conjunto de datos contiene 60.000 imágenes, y cada imagen tiene un tamaño de 32 por 32 píxeles y 3 canales de color (RGB). El tamaño del conjunto de datos completo es de 175 MB. Según la conexión a Internet, el proceso de descarga puede tardar algún tiempo.
datadir = tempdir; downloadCIFARData(datadir);
Cargue el conjunto de datos CIFAR-10 como imágenes y etiquetas de entrenamiento, y como imágenes y etiquetas de prueba. Para habilitar la validación de la red, use 5.000 de las imágenes de prueba para la validación.
[XTrain,YTrain,XTest,YTest] = loadCIFARData(datadir); idx = randperm(numel(YTest),5000); XValidation = XTest(:,:,:,idx); XTest(:,:,:,idx) = []; YValidation = YTest(idx); YTest(idx) = [];
Puede visualizar una muestra de las imágenes de entrenamiento usando el código siguiente.
figure; idx = randperm(numel(YTrain),20); for i = 1:numel(idx) subplot(4,5,i); imshow(XTrain(:,:,:,idx(i))); end
Elegir las variables que desea optimizar
Especifique las variables que desea optimizar usando la optimización bayesiana y especifique los intervalos en los que se debe buscar. Especifique también si las variables son enteros y si desea buscar el intervalo en espacio logarítmico. Optimice las variables siguientes:
Profundidad de la sección de la red. Este parámetro controla la profundidad de la red. La red tiene tres secciones, cada una con capas convolucionales idénticas
SectionDepth. El número total de capas convolucionales es3*SectionDepth. La función objetivo más adelante en el script toma el número de filtros convolucionales en cada capa proporcional a1/sqrt(SectionDepth). Como resultado, el número de parámetros y la cantidad de cálculo requeridos para cada iteración son aproximadamente iguales para diferentes profundidades de sección.Tasa de aprendizaje inicial. La mejor tasa de aprendizaje puede depender de sus datos, así como de la red que está entrenando.
Momento del gradiente descendente estocástico. El momento añade inercia a las actualizaciones de los parámetros haciendo que la actualización actual contenga una contribución proporcional a la actualización en la iteración anterior. Esto da como resultado actualizaciones de parámetros más suaves y una reducción del ruido inherente al gradiente descendente estocástico.
Intensidad de regularización L2. Utilice la regularización para evitar el sobreajuste. Busque el espacio de intensidad de regularización para encontrar un buen valor. El aumento de datos y la normalización de lotes también ayudan a regularizar la red.
optimVars = [
optimizableVariable('SectionDepth',[1 3],'Type','integer')
optimizableVariable('InitialLearnRate',[1e-2 1],'Transform','log')
optimizableVariable('Momentum',[0.8 0.98])
optimizableVariable('L2Regularization',[1e-10 1e-2],'Transform','log')];Realizar una optimización bayesiana
Cree la función objetivo para el optimizador bayesiano utilizando los datos de entrenamiento y validación como entradas. La función objetivo entrena una red neuronal convolucional y devuelve el error de clasificación en el conjunto de validación. Esta función se define al final de este script. Puesto que bayesopt utiliza la tasa de error en el conjunto de validación para elegir el mejor modelo, es posible que la red final sobreajuste el conjunto de validación. El modelo final seleccionado se prueba en el conjunto de prueba independiente para hacer una estimación del error de generalización.
ObjFcn = makeObjFcn(XTrain,YTrain,XValidation,YValidation);
Realice la optimización bayesiana minimizando el error de clasificación en el conjunto de validación. Especifique el tiempo de optimización total en segundos. Para aprovechar al máximo la potencia de la optimización bayesiana, se deben realizar al menos 30 evaluaciones de la función objetivo. Para entrenar redes en paralelo en múltiples unidades GPU, establezca el valor de 'UseParallel' en true. Si dispone de una sola GPU y establece el valor 'UseParallel' en true, todos los workers comparten esa GPU y no se aumenta la velocidad de entrenamiento, pero sí aumentan las posibilidades de que la GPU se quede sin memoria.
Después de que cada red finalice el entrenamiento, bayesopt imprime los resultados en la ventana de comandos. Entonces, la función bayesopt devuelve los nombres de archivo en BayesObject.UserDataTrace. La función objetivo guarda las redes entrenadas en el disco y devuelve los nombres de archivo a bayesopt.
BayesObject = bayesopt(ObjFcn,optimVars, ... 'MaxTime',14*60*60, ... 'IsObjectiveDeterministic',false, ... 'UseParallel',false);
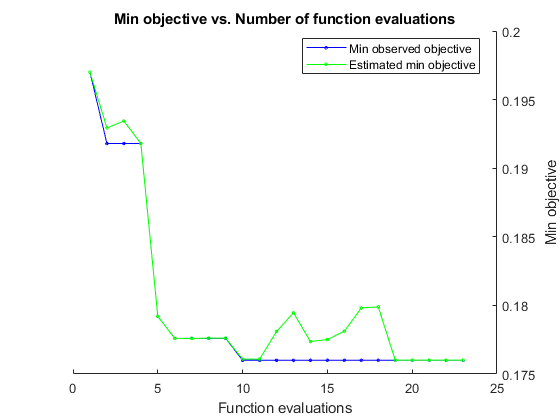
|===================================================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | SectionDepth | InitialLearn-| Momentum | L2Regulariza-| | | result | | runtime | (observed) | (estim.) | | Rate | | tion | |===================================================================================================================================| | 1 | Best | 0.197 | 955.69 | 0.197 | 0.197 | 3 | 0.61856 | 0.80624 | 0.00035179 |
| 2 | Best | 0.1918 | 790.38 | 0.1918 | 0.19293 | 2 | 0.074118 | 0.91031 | 2.7229e-09 |
| 3 | Accept | 0.2438 | 660.29 | 0.1918 | 0.19344 | 1 | 0.051153 | 0.90911 | 0.00043113 |
| 4 | Accept | 0.208 | 672.81 | 0.1918 | 0.1918 | 1 | 0.70138 | 0.81923 | 3.7783e-08 |
| 5 | Best | 0.1792 | 844.07 | 0.1792 | 0.17921 | 2 | 0.65156 | 0.93783 | 3.3663e-10 |
| 6 | Best | 0.1776 | 851.49 | 0.1776 | 0.17759 | 2 | 0.23619 | 0.91932 | 1.0007e-10 |
| 7 | Accept | 0.2232 | 883.5 | 0.1776 | 0.17759 | 2 | 0.011147 | 0.91526 | 0.0099842 |
| 8 | Accept | 0.2508 | 822.65 | 0.1776 | 0.17762 | 1 | 0.023919 | 0.91048 | 1.0002e-10 |
| 9 | Accept | 0.1974 | 1947.6 | 0.1776 | 0.17761 | 3 | 0.010017 | 0.97683 | 5.4603e-10 |
| 10 | Best | 0.176 | 1938.4 | 0.176 | 0.17608 | 2 | 0.3526 | 0.82381 | 1.4244e-07 |
| 11 | Accept | 0.1914 | 2874.4 | 0.176 | 0.17608 | 3 | 0.079847 | 0.86801 | 9.7335e-07 |
| 12 | Accept | 0.181 | 2578 | 0.176 | 0.17809 | 2 | 0.35141 | 0.80202 | 4.5634e-08 |
| 13 | Accept | 0.1838 | 2410.8 | 0.176 | 0.17946 | 2 | 0.39508 | 0.95968 | 9.3856e-06 |
| 14 | Accept | 0.1786 | 2490.6 | 0.176 | 0.17737 | 2 | 0.44857 | 0.91827 | 1.0939e-10 |
| 15 | Accept | 0.1776 | 2668 | 0.176 | 0.17751 | 2 | 0.95793 | 0.85503 | 1.0222e-05 |
| 16 | Accept | 0.1824 | 3059.8 | 0.176 | 0.17812 | 2 | 0.41142 | 0.86931 | 1.447e-06 |
| 17 | Accept | 0.1894 | 3091.5 | 0.176 | 0.17982 | 2 | 0.97051 | 0.80284 | 1.5836e-10 |
| 18 | Accept | 0.217 | 2794.5 | 0.176 | 0.17989 | 1 | 0.2464 | 0.84428 | 4.4938e-06 |
| 19 | Accept | 0.2358 | 4054.2 | 0.176 | 0.17601 | 3 | 0.22843 | 0.9454 | 0.00098248 |
| 20 | Accept | 0.2216 | 4411.7 | 0.176 | 0.17601 | 3 | 0.010847 | 0.82288 | 2.4756e-08 |
|===================================================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | SectionDepth | InitialLearn-| Momentum | L2Regulariza-| | | result | | runtime | (observed) | (estim.) | | Rate | | tion | |===================================================================================================================================| | 21 | Accept | 0.2038 | 3906.4 | 0.176 | 0.17601 | 2 | 0.09885 | 0.81541 | 0.0021184 |
| 22 | Accept | 0.2492 | 4103.4 | 0.176 | 0.17601 | 2 | 0.52313 | 0.83139 | 0.0016269 |
| 23 | Accept | 0.1814 | 4240.5 | 0.176 | 0.17601 | 2 | 0.29506 | 0.84061 | 6.0203e-10 |
__________________________________________________________
Optimization completed.
MaxTime of 50400 seconds reached.
Total function evaluations: 23
Total elapsed time: 53088.5123 seconds
Total objective function evaluation time: 53050.7026
Best observed feasible point:
SectionDepth InitialLearnRate Momentum L2Regularization
____________ ________________ ________ ________________
2 0.3526 0.82381 1.4244e-07
Observed objective function value = 0.176
Estimated objective function value = 0.17601
Function evaluation time = 1938.4483
Best estimated feasible point (according to models):
SectionDepth InitialLearnRate Momentum L2Regularization
____________ ________________ ________ ________________
2 0.3526 0.82381 1.4244e-07
Estimated objective function value = 0.17601
Estimated function evaluation time = 1898.2641
Evaluar la red final
Cargue la mejor red encontrada en la optimización y su precisión de validación.
bestIdx = BayesObject.IndexOfMinimumTrace(end);
fileName = BayesObject.UserDataTrace{bestIdx};
savedStruct = load(fileName);
valError = savedStruct.valErrorvalError = 0.1760
Prediga las etiquetas del conjunto de prueba y calcule el error de prueba. Trate la clasificación de cada imagen del conjunto de prueba como eventos independientes con una cierta probabilidad de éxito, lo que significa que el número de imágenes clasificadas incorrectamente sigue una distribución binomial. Úselo para calcular el error estándar (testErrorSE) y un intervalo de confianza aproximado del 95% (testError95CI) de la tasa de error de generalización. Este método a menudo se conoce como método de Wald. bayesopt determina la mejor red utilizando el conjunto de validación sin exponer la red al conjunto de prueba. Entonces, es posible que el error en la prueba sea superior que el error en la validación.
[YPredicted,probs] = classify(savedStruct.trainedNet,XTest); testError = 1 - mean(YPredicted == YTest)
testError = 0.1910
NTest = numel(YTest); testErrorSE = sqrt(testError*(1-testError)/NTest); testError95CI = [testError - 1.96*testErrorSE, testError + 1.96*testErrorSE]
testError95CI = 1×2
0.1801 0.2019
Represente la matriz de confusión para los datos de prueba. Muestre la precisión y la recuperación de cada clase mediante el uso de resúmenes de columnas y filas.
figure('Units','normalized','Position',[0.2 0.2 0.4 0.4]); cm = confusionchart(YTest,YPredicted); cm.Title = 'Confusion Matrix for Test Data'; cm.ColumnSummary = 'column-normalized'; cm.RowSummary = 'row-normalized';

Puede mostrar algunas imágenes de prueba junto con sus clases predichas y las probabilidades de esas clases usando el código siguiente:
figure idx = randperm(numel(YTest),9); for i = 1:numel(idx) subplot(3,3,i) imshow(XTest(:,:,:,idx(i))); prob = num2str(100*max(probs(idx(i),:)),3); predClass = char(YPredicted(idx(i))); label = [predClass,', ',prob,'%']; title(label) end
Función objetivo para optimización
Defina la función objetivo para optimización. Esta función lleva a cabo los pasos siguientes:
Toma los valores de las variables de optimización como entradas.
bayesoptllama a la función objetivo con los valores actuales de las variables de optimización en una tabla en la que cada nombre de columna es igual al nombre de la variable. Por ejemplo, el valor actual de la profundidad de la sección de la red esoptVars.SectionDepth.Define la arquitectura de la red y las opciones de entrenamiento.
Valida y entrena la red.
Guarda la red entrenada, el error de validación y las opciones de entrenamiento en el disco.
Devuelve el error de validación y el nombre del archivo donde se ha guardado la red.
function ObjFcn = makeObjFcn(XTrain,YTrain,XValidation,YValidation) ObjFcn = @valErrorFun; function [valError,cons,fileName] = valErrorFun(optVars)
Defina la arquitectura de la red neuronal convolucional.
Añada relleno a las capas convolucionales de manera que el tamaño espacial de salida sea siempre el mismo que el tamaño de entrada.
Cada vez que reduzca las dimensiones espaciales por un factor de dos utilizando capas de agrupamiento máximo, aumente la cantidad de filtros por un factor de dos. Esto asegura que la cantidad de cálculos requeridos en cada capa convolucional sea aproximadamente la misma.
Elija el número de filtros proporcional a
1/sqrt(SectionDepth), de manera que las redes de diferentes profundidades tengan aproximadamente el mismo número de parámetros y requieran aproximadamente la misma cantidad de cálculos por iteración. Para aumentar el número de parámetros de la red y la flexibilidad general de la red, aumentenumF. Para entrenar redes aún más profundas, cambie el intervalo de la variableSectionDepth.Utilice
convBlock(filterSize,numFilters,numConvLayers)para crear un bloque de capas convolucionalesnumConvLayers, cada una con unfilterSizeconcreto y filtrosnumFilters, que además van seguidos de una capa de normalización de lotes y una capa ReLU. La funciónconvBlockse define al final de este ejemplo.
imageSize = [32 32 3];
numClasses = numel(unique(YTrain));
numF = round(16/sqrt(optVars.SectionDepth));
layers = [
imageInputLayer(imageSize)
% The spatial input and output sizes of these convolutional
% layers are 32-by-32, and the following max pooling layer
% reduces this to 16-by-16.
convBlock(3,numF,optVars.SectionDepth)
maxPooling2dLayer(3,'Stride',2,'Padding','same')
% The spatial input and output sizes of these convolutional
% layers are 16-by-16, and the following max pooling layer
% reduces this to 8-by-8.
convBlock(3,2*numF,optVars.SectionDepth)
maxPooling2dLayer(3,'Stride',2,'Padding','same')
% The spatial input and output sizes of these convolutional
% layers are 8-by-8. The global average pooling layer averages
% over the 8-by-8 inputs, giving an output of size
% 1-by-1-by-4*initialNumFilters. With a global average
% pooling layer, the final classification output is only
% sensitive to the total amount of each feature present in the
% input image, but insensitive to the spatial positions of the
% features.
convBlock(3,4*numF,optVars.SectionDepth)
averagePooling2dLayer(8)
% Add the fully connected layer and the final softmax and
% classification layers.
fullyConnectedLayer(numClasses)
softmaxLayer
classificationLayer];Especifique opciones para el entrenamiento de la red. Optimice la tasa de aprendizaje inicial, el momento de SGD y la intensidad de regularización L2.
Especifique los datos de validación y elija el valor 'ValidationFrequency' de tal manera que trainNetwork valide la red una vez por época. Entrene durante un número fijo de épocas y reduzca la tasa de aprendizaje 10 veces durante las últimas épocas. Esto reduce el ruido de las actualizaciones de los parámetros y permite que los parámetros de la red se establezcan más cerca de un mínimo de la función de pérdida.
miniBatchSize = 256;
validationFrequency = floor(numel(YTrain)/miniBatchSize);
options = trainingOptions('sgdm', ...
'InitialLearnRate',optVars.InitialLearnRate, ...
'Momentum',optVars.Momentum, ...
'MaxEpochs',60, ...
'LearnRateSchedule','piecewise', ...
'LearnRateDropPeriod',40, ...
'LearnRateDropFactor',0.1, ...
'MiniBatchSize',miniBatchSize, ...
'L2Regularization',optVars.L2Regularization, ...
'Shuffle','every-epoch', ...
'Verbose',false, ...
'Plots','training-progress', ...
'ValidationData',{XValidation,YValidation}, ...
'ValidationFrequency',validationFrequency);Utilice el aumento de datos para voltear aleatoriamente las imágenes de entrenamiento a lo largo del eje vertical y trasladarlas aleatoriamente hasta cuatro píxeles horizontal y verticalmente. El aumento de datos ayuda a evitar que la red se sobreajuste y memorice los detalles exactos de las imágenes de entrenamiento.
pixelRange = [-4 4];
imageAugmenter = imageDataAugmenter( ...
'RandXReflection',true, ...
'RandXTranslation',pixelRange, ...
'RandYTranslation',pixelRange);
datasource = augmentedImageDatastore(imageSize,XTrain,YTrain,'DataAugmentation',imageAugmenter);Entrene la red y represente el progreso del entrenamiento durante el mismo. Cierre todas las gráficas de entrenamiento una vez que finalice el entrenamiento.
trainedNet = trainNetwork(datasource,layers,options);
close(findall(groot,'Tag','NNET_CNN_TRAININGPLOT_UIFIGURE'))
Evalúe la red entrenada en el conjunto de validación, calcule las etiquetas de imagen predichas y calcule la tasa de error en los datos de validación.
YPredicted = classify(trainedNet,XValidation);
valError = 1 - mean(YPredicted == YValidation);Cree un nombre de archivo que contenga el error de validación y guarde la red, el error de validación y las opciones de entrenamiento en el disco. La función objetivo devuelve fileName como un argumento de salida y bayesopt devuelve todos los nombres de archivo de BayesObject.UserDataTrace. El argumento de salida requerido cons adicional especifica las restricciones incluidas en las variables. No hay restricciones de variables.
fileName = num2str(valError) + ".mat"; save(fileName,'trainedNet','valError','options') cons = []; end end
La función convBlock crea un bloque de capas convolucionales numConvLayers, cada una con un filterSize concreto y filtros numFilters, que además van seguidos de una capa de normalización de lotes y una capa ReLU.
function layers = convBlock(filterSize,numFilters,numConvLayers) layers = [ convolution2dLayer(filterSize,numFilters,'Padding','same') batchNormalizationLayer reluLayer]; layers = repmat(layers,numConvLayers,1); end
Referencias
[1] Krizhevsky, Alex. "Learning multiple layers of features from tiny images." (2009). https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf
Consulte también
Experiment Manager | trainnet | trainingOptions | dlnetwork | bayesopt (Statistics and Machine Learning Toolbox)