Moving Variance
Moving variance
Libraries:
DSP System Toolbox /
Statistics
Description
The Moving Variance block computes the moving variance of the input signal along each channel independently over time. The block uses either the sliding window method or the exponential weighting method to compute the moving variance. In the sliding window method, a window of specified length moves over the data sample by sample, and the block computes the variance over the data in the window. In the exponential weighting method, the block subtracts each sample of the data from the average, squares the difference, and multiplies the squared result by a weighting factor. The block then computes the variance by adding all the weighted data. For more details on these methods, see Algorithms.
Examples
Compute Moving Variance of Noisy Square Wave Signal
Compare the sliding window variance method and the exponentially weighted variance method in Simulink® using the Moving Variance block.
Ports
Input
The block computes the moving variance of the data specified at this input port. Specify real- or complex-valued multichannel inputs of the size m-by-n, where m ≥ 1 and n ≥ 1.
When the Allow arbitrary frame length for fixed-size input signals parameter appears and is not selected, and you input a fixed-size signal, the frame length must be a multiple of the hop size (window length − overlap length). In all other cases, the input frame length can be arbitrary.
The block accepts variable-size inputs (frame length changes during simulation). When you input a variable-size signal, the frame length of the signal can be arbitrary.
This port is unnamed until you set Method to
Exponential weighting and select the Specify forgetting
factor from input port parameter.
Data Types: single | double
Complex Number Support: Yes
Specify the forgetting factor as a non-negative real scalar in the range [0,1]. The forgetting factor determines how much weight past data is given. A forgetting factor of 0.9 gives more weight to the older data than does a forgetting factor of 0.1. A forgetting factor of 1.0 indicates infinite memory and all previous samples are given an equal weight. A forgetting factor of 0 indicates no memory and the past samples have no weight on the current computation.
Dependencies
This port appears when you set Method to Exponential
weighting and select the Specify forgetting factor from input
port parameter.
Data Types: single | double
Output
Moving variance output, returned as a vector or a matrix. The block computes the moving variance based on the Method parameter settings using either the sliding window method or the exponential weighting method. For more details, see Algorithms.
This table provides more details on the dimensions of the output signal.
| Input Signal | Input Dimensions | Output Dimensions When Allow arbitrary frame length for fixed-size input signals Appears | Output Dimensions When Allow arbitrary frame length for fixed-size input signals Does Not Appear |
|---|---|---|---|
| Fixed-size signal | m-by-n, where m is a multiple of the hop size (window length − overlap length) | (m/hop size)-by-n | m-by-n |
| Fixed-size signal | m-by-n, where m is not a multiple of the hop size (window length − overlap length) |
If you do not select Allow arbitrary frame length for fixed-size input signals, the block errors. | m-by-n |
| Variable-size signal | m-by-n | ceil(m/hop
size)-by-n | m-by-n |
When the output has an upper bound size of
ceil(m/hop size)-by-n, during
simulation, the size of the first dimension varies within this bound and the size of the
second dimension remains constant. For an example that shows this behavior, see Compute Moving Variance of Noisy Square Wave Signal.
Data Types: single | double
Complex Number Support: Yes
Parameters
If a parameter is listed as tunable, then you can change its value during simulation.
Sliding window— A window of length Window length moves over the input data along each channel. For every sample the window moves over, the block computes the variance over the data in the window.Exponential weighting— The block subtracts each sample of the data from the average, squares the difference, and multiplies the squared result by a weighting factor. The block then computes the variance by adding all the weighted data. The magnitude of the weighting factors decreases exponentially as the age of the data increases, but the magnitude never reaches zero.
For more details on these methods, see Algorithms.
When you select this check box, the length of the sliding window is equal to the value you specify in Window length. When you clear this check box, the length of the sliding window is infinite. In this mode, the block computes the variance of the current sample with respect to all the previous samples in the channel.
Dependencies
To enable this parameter, set Method to Sliding
window.
Specifies the length of the sliding window in samples.
Dependencies
To enable this parameter, set Method to Sliding
window and select the Specify window length check
box.
Specify the overlap length between sliding windows as a nonnegative integer. The value of overlap length varies in the range [0, Window length − 1].
Dependencies
To enable this parameter, set Method to Sliding
window and select the Specify window length check
box.
Specify whether fixed-size input signals (whose size does not change during simulation) can have an arbitrary frame length, where the frame length does not have to be a multiple of the hop size. Hop size is defined as Window length − Overlap length. The block uses this parameter setting only for fixed-size input signals and ignores this parameter if the input has a variable-size.
When the input signal is a variable-size signal, the signal can have arbitrary frame length, that is, the frame length does not have to be a multiple of the hop size.
For fixed-size input signals, if you:
Select the Allow arbitrary frame length for fixed-size input signals parameter, the frame length of the signal does not have to be a multiple of the hop size. If the input is not a multiple of the hop size, then the output is generally a variable-size signal. Therefore, to support arbitrary input size, the block must also support variable-size operations, which you can enable by selecting the Allow arbitrary frame length for fixed-size input signals parameter.
Clear the Allow arbitrary frame length for fixed-size input signals parameter, the input frame length must be a multiple of the hop size.
Dependencies
To enable this parameter, set Method to Sliding
window and select the Specify window length check
box.
When you select this check box, the forgetting factor is input through the lambda port. When you clear this check box, the forgetting factor is specified on the block dialog through the Forgetting factor parameter.
Dependencies
To enable this parameter, set Method to Exponential
weighting.
Specify the exponential weighting factor as a non-negative real scalar in the range [0,1]. This value determines how much weight the past data is given. A forgetting factor of 0.9 gives more weight to the older data than does a forgetting factor of 0.1. A forgetting factor of 1.0 indicates infinite memory and all the past samples are given an equal weight. A forgetting factor of 0 indicates no memory and the past samples have no weight on the current computation.
Tunable: Yes
Dependencies
To enable this parameter, set Method to Exponential
weighting and clear the Specify forgetting factor from input
port check box.
Specify the type of simulation to run. You can set this parameter to:
Interpreted execution–– Simulate model using the MATLAB® interpreter. This option shortens startup time.Code generation–– Simulate model using generated C code. The first time you run a simulation, Simulink generates C code for the block. The C code is reused for subsequent simulations as long as the model does not change. This option requires additional startup time but provides faster subsequent simulations.
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Algorithms
In the sliding window method, the output at the current sample is the variance of the current sample with respect to the data in the window. To compute the first output sample, the algorithm waits until it receives the hop size number of input samples. Hop size is defined as window length – overlap length. Remaining samples in the window are considered to be zero. As an example, if the window length is 5 and the overlap length is 2, then the algorithm waits until it receives 3 samples of input to compute the first sample of the output. After generating the first output, it generates the subsequent output samples for every hop size number of input samples.
When you do not specify the window length, the algorithm chooses an infinite window length. In this mode, the output is the moving variance of the current sample with respect to all previous samples in the channel.
Consider an example of computing the moving variance of a streaming input data using the sliding window method. The algorithm uses a window length of 4 and an overlap length of 3. With each input sample that comes in, the window of length 4 moves along the data.

In the exponential weighting method, the moving variance is computed recursively using these formulas:
To compute the moving variance, the algorithm implements these equations recursively.
— Moving variance of the current data sample with respect to the rest of the data in the channel.
— Moving average at the current sample. For details on computing the moving average, see
dsp.MovingAverage.— Difference between each data sample and the average of the data, squared.
— Difference between each data sample and the average of the data, squared and multiplied with the forgetting factor. All the squared terms are added.
— Weighting factor applied to the sum.
λ — Forgetting factor you can specify through the
ForgettingFactorproperty.
As the age of the data increases, the magnitude of the weighting factor decreases exponentially, and never reaches zero. In other words, the recent data has more influence on the current variance, than the older data.
The value of the forgetting factor determines the rate of change of the weighting factors. A forgetting factor of 0.9 gives more weight to the older data than does a forgetting factor of 0.1. A forgetting factor of 1.0 indicates infinite memory. All the past samples are given an equal weight.
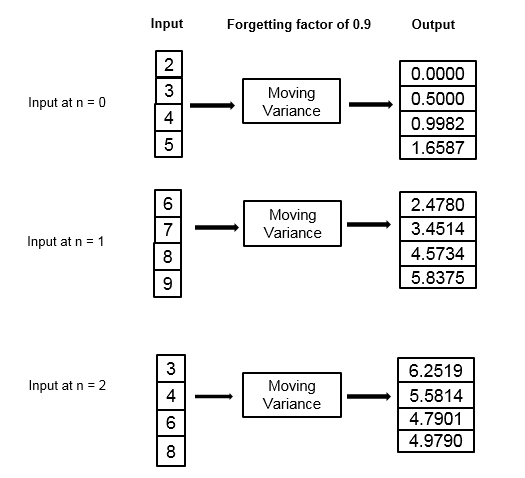
Consider an example of computing the moving variance using the exponential weighting method. The forgetting factor is 0.9.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2016bYou can now specify a forgetting factor of 0 in the Moving Variance block.
The default value of the Simulate using parameter is now
Interpreted execution. With this change, the block uses the
MATLAB interpreter for simulation by default.
Starting in R2022b, you can specify the overlap length between sliding windows using the Overlap length parameter.
Moving Variance block supports input signals with arbitrary frame lengths when the:
Input signal is a fixed-size signal (frame length does not change during simulation) and you select the Allow arbitrary frame length for fixed-size input signals parameter (if enabled).
Input signal is a variable-size signal (frame length changes during simulation).
When this block supports an arbitrary frame length input signal, the input frame length does not have to be a multiple of the hop size.
See Also
Blocks
- Variance | Moving Average | Moving Maximum | Moving Minimum | Moving Standard Deviation | Moving RMS | Median Filter
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
