lifetableconv

Convert life table series into life tables with forced termination

Syntax

[qx,lx,dx] = lifetableconv(x0,lx0)

[qx,lx,dx] = lifetableconv(x0,y0,y0type)

Description

[qx,lx,dx] = lifetableconv(x0,lx0) converts life table with ages x0 and survival counts lx0 into life tables with termination.

[qx,lx,dx] = lifetableconv(x0,y0,y0type) converts life table with ages x0 and series y0, specified by the optional argument y0type, into life tables with termination.

Examples

Convert Life Table Series into Life Tables with Forced Termination

Load the life table data file.

load us_lifetable_2009

Convert life table series into life tables with forced termination.

[qx,lx,dx] = lifetableconv(x,lx);
display(qx(1:20,:))

    0.0064    0.0070    0.0057
    0.0004    0.0004    0.0004
    0.0003    0.0003    0.0002
    0.0002    0.0002    0.0002
    0.0002    0.0002    0.0001
    0.0001    0.0002    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0002    0.0002    0.0002
    0.0003    0.0004    0.0002
    0.0004    0.0005    0.0002
    0.0005    0.0006    0.0003
    0.0005    0.0007    0.0003
    0.0006    0.0009    0.0004
    0.0007    0.0010    0.0004

display(lx(1:20,:))

   1.0e+05 *

    1.0000    1.0000    1.0000
    0.9936    0.9930    0.9943
    0.9932    0.9926    0.9939
    0.9930    0.9923    0.9937
    0.9927    0.9920    0.9935
    0.9926    0.9919    0.9933
    0.9924    0.9917    0.9932
    0.9923    0.9916    0.9931
    0.9922    0.9914    0.9930
    0.9921    0.9913    0.9929
    0.9920    0.9912    0.9928
    0.9919    0.9911    0.9927
    0.9918    0.9910    0.9926
    0.9917    0.9909    0.9925
    0.9915    0.9907    0.9923
    0.9912    0.9903    0.9921
    0.9908    0.9898    0.9919
    0.9904    0.9892    0.9916
    0.9899    0.9885    0.9913
    0.9892    0.9876    0.9909

display(dx(1:20,:))

  637.2266  698.8750  572.6328
   40.4062   43.9297   36.7188
   27.1875   30.0938   24.1406
   20.7656   23.0781   18.3359
   15.9141   17.2109   14.5625
   14.8672   16.3125   13.3516
   13.3672   14.7891   11.8750
   12.1328   13.3828   10.8203
   10.8125   11.6094    9.9844
    9.4609    9.5781    9.3438
    8.6172    8.1328    9.1172
    9.2656    8.8359    9.7188
   12.5938   13.5078   11.6328
   19.1016   22.9844   15.0234
   27.6719   35.5938   19.3516
   36.6328   48.5703   24.0547
   45.0156   60.7109   28.4844
   53.1406   72.8906   32.2812
   60.8984   85.1172   35.2578
   68.3438   97.2266   37.6875

Plot the qx series and display the legend. The series qx is the conditional probability that a person at age x will die between age x and the next age in the series.

plot(x,log(qx))
legend(series)

Convert the Life Table dx Series After Fitting and Generating the Life Table Series

Load the life table data file.

load us_lifetable_2009

Calibrate life table from survival data with the default Heligman-Pollard parametric model.

a = lifetablefit(x,lx)

a = 8×3

    0.0005    0.0006    0.0004
    0.0592    0.0819    0.0192
    0.1452    0.1626    0.1048
    0.0007    0.0011    0.0007
    6.2846    6.7639    1.1036
   24.1387   24.2894   53.1854
    0.0000    0.0000    0.0000
    1.0971    1.0987    1.1100

Generate life table series from the calibrated mortality model.

qx = lifetablegen((0:120),a);
display(qx(1:20,:))

    0.0063    0.0069    0.0057
    0.0005    0.0006    0.0004
    0.0002    0.0003    0.0002
    0.0002    0.0002    0.0002
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0001    0.0001    0.0001
    0.0002    0.0002    0.0001
    0.0002    0.0002    0.0002
    0.0002    0.0003    0.0002
    0.0003    0.0004    0.0002
    0.0004    0.0005    0.0002
    0.0005    0.0006    0.0003
    0.0006    0.0008    0.0003
    0.0007    0.0009    0.0003

Convert life table series into life tables with forced termination.

[~,~,dx] = lifetableconv((0:120),qx,'qx');
display(dx(1:20,:))

  630.9933  686.9434  571.6093
   48.7925   55.1036   40.9874
   24.8017   26.3779   23.6167
   17.0832   17.5878   17.0316
   13.6182   13.8187   13.6141
   11.8663   12.0075   11.6313
   10.9783   11.1572   10.4904
   10.5997   10.8604    9.9488
   10.5758   10.9396    9.8952
   10.8790   11.3612   10.2718
   11.6084   12.2508   11.0419
   12.9920   13.9271   12.1765
   15.3475   16.8834   13.6483
   18.9931   21.6791   15.4302
   24.1383   28.7663   17.4944
   30.7995   38.3212   19.8134
   38.7704   50.1487   22.3603
   47.6526   63.6908   25.1098
   56.9296   78.1271   28.0385
   66.0576   92.5261   31.1257

Plot the dx series and display the legend. The series dx is the number of people who die out of 100,000 alive at birth between age x and the next age in the series.

plot((0:119),dx(1:end-1,:));
legend(series, 'location', 'northwest');
title('\bfLife Table Yearly Decrements');
xlabel('Age');
ylabel('Number Dying within a Given Year');

Input Arguments

x0 — Increasing ages for raw data

vector of nonnegative integer values

Increasing ages for raw data, specified as nonnegative integer values in an N0 vector.

The vector of ages x must contain nonnegative integer values. If the input series is the discrete survival function lx, then the starting age need only be nonnegative. Otherwise, the starting age must be 0.

Data Types: double

lx0 — Collection of num standardized survivor series

matrix

Collection of num standardized survivor series, specified as an N0-by-num matrix. The input lx0 series is the number of people alive at age x, given 100,000 alive at birth. Values of 0 or NaN in the input table lx0 are ignored.

Data Types: double

y0 — Collection of num life table series to be converted

matrix

Collection of num life table series to be converted, specified as an N0-by-num matrix. The default y0 series is lx0.

Data Types: double

y0type — Type of mortality series for input y0 with default 'lx'

'lx' (default) | character vector with values 'qx', 'lx', 'dx'

(Optional) Type of mortality series for input y0, specified as a character vector with one of the following values:

• 'qx' — Input is a table of discrete hazards (qx).

• 'lx' — Input is a table of discrete survival counts (lx).

• 'dx' — Input is a table of discrete decrements (dx).

Whereas the output series have forced termination, the input series (y0) can have one of several types of termination:

• Natural termination runs out to the last person so that lx goes to 0, qx goes to 1, and dx goes to 0. For more information, see Natural Termination.

• Truncated termination stops at a terminal age so that lx is positive, qx is less than 1, and dx is positive. Any ages after the terminal age are NaN values. For more information, see Truncated Termination.

Data Types: char

Output Arguments

qx — Discrete hazard function

matrix

Discrete hazard function, returned as an N0-by-num matrix with forced termination. For more information, see Forced Termination.

The series qx is the conditional probability that a person at age x will die between age x and the next age in the series.

lx — Discrete survival function

matrix

Discrete survival function, returned as an N0-by-num matrix with forced termination. For more information, see Forced Termination.

The series lx is the number of people alive at age x, given 100,000 alive at birth.

dx — Discrete decrements function

matrix

Discrete decrements function, returned as an N0-by-num matrix with forced termination. For more information, see Forced Termination.

The series dx is the number of people who die out of 100,000 alive at birth, between age x and the next age in the series.

More About

Life Table

A life table is a statistical table used in demography and actuarial science to summarize the mortality experience of a population.

A life table provides a detailed breakdown of the probability of death and survival at various ages, allowing for the analysis of life expectancy and the assessment of the health status of a population.

Forced Termination

Most modern life tables have “forced” termination. Forced termination means that the last row of the life table applies for all persons with ages on or after the last age in the life table.

This sample illustrates forced termination.

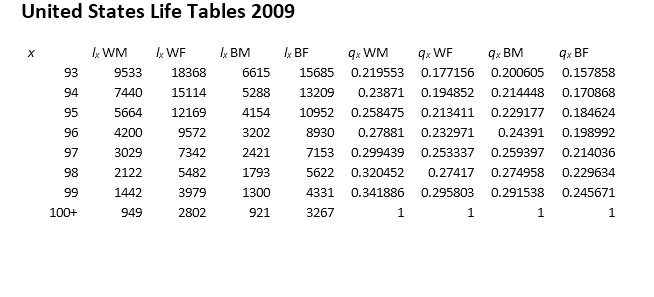
In this case, the last row of the life table applies for all persons aged 100 or older. Specifically, q_x probabilities are ₁q_x for ages less than 100 and, technically, _∞q_x for age 100.

Forced termination has terminal age values that apply to all ages after the terminal age so that lx is positive, qx is 1, and dx is positive. Ages after the terminal age are NaN values, although lx and dx can be 0 and qx can be 1 for input series. Forced termination is triggered by a naturally terminating series, the last age in a truncated series, or the first NaN value in a series.

Natural Termination

Before 1970, life tables were often published with data that included all ages for which persons associated with a given series were still alive. Tables in this form have "natural" termination. In natural termination, the last row of the life table for each series counts the deaths or probabilities of deaths of the last remaining person at the corresponding age. Tables in this form can be problematic due to the granularity of the data and the fact that groups of series can terminate at distinct ages. Natural termination is illustrated in the following sample of the last few years of a life table.

This form for life tables poses a number of issues that go beyond the obvious statistical issues. First, the l_x table on the left terminates at ages 108, 109, 109, and 113 for the four series in the table. Technically, the numbers after these ages are 0, but can also be NaN values because no person is alive after these terminating ages. Second, the probabilities q_x on the right terminate with fluctuating probabilities that go from 0 to 1 in some cases. In this case, however, all probabilities are ₁q_x probabilities (unlike the forced termination probabilities). You can argue that the probabilities after the ages of termination can be 1 (anyone alive at this age is expected to die in the next year), 0 (the age lies outside the support of the probability distribution), or NaN values.

Truncated Termination

Truncated termination occurs with truncation of life tables at an arbitrary age. For example, from 1970–1990, United States life tables truncated at age 85. This format is problematic because life table probabilities must either terminate with probability 1 (forced termination) or discard data that exceeds the terminating age. This sample of the last few years of a life table illustrates truncated termination. The raw data for this table is the l_x series. The q_x series is derived from this series.

This life table format poses problems for termination because, for example, over 27% of the population for the fourth l_x series is still alive at age 85. To claim that the probability of dying for all ages after age 85 is 100% might be true but is uninformative. Notwithstanding the statistical issues, however, tables in this form are completed by forced termination.

References

[1] Arias, E. “United States Life Tables.” National Vital Statistics Reports, U.S. Department of Health and Human Services. Vol. 62, No. 7, 2009.

Version History

Introduced in R2015a