lifetablegen
Generate life table series from calibrated mortality model
Description
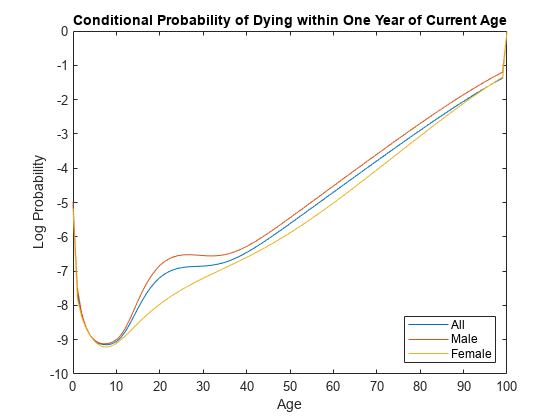
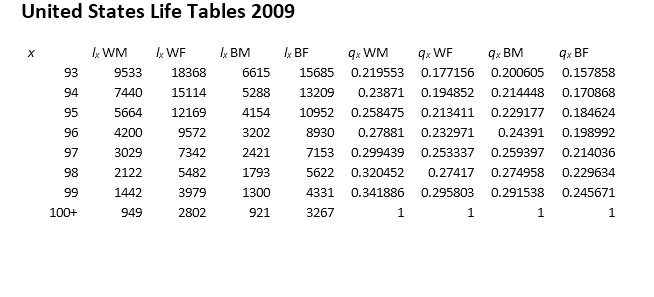
Examples
Input Arguments
Output Arguments
More About
References
[1] Arias, E. “United States Life Tables.” National Vital Statistics Reports, U.S. Department of Health and Human Services. Vol. 62, No. 7, 2009.
[2] Carriere, F. “Parametric Models for Life Tables.” Transactions of the Society of Actuaries. Vol. 44, 1992, pp. 77–99.
[3] Gompertz, B. “On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies.” Philosophical Transactions of the Royal Society. Vol. 115, 1825, pp. 513–582.
[4] Heligman, L. M. A., and J. H. Pollard. “The Age Pattern of Mortality.” Journal of the Institute of Actuaries Vol. 107, Pt. 1, 1980, pp. 49–80.
[5] Makeham, W. M. “On the Law of Mortality and the Construction of Annuity Tables.” Journal of the Institute of Actuaries Vol. 8, 1860, pp. 301–310.
[6] Siler, W. “A Competing-Risk Model for Animal Mortality.” Ecology Vol. 60, pp. 750–757, 1979.
[7] Siler, W. “Parameters of Mortality in Human Populations with Widely Varying Life Spans.” Statistics in Medicine Vol. 2, 1983, pp. 373–380.
Version History
Introduced in R2015a