Frente de Pareto para optimización multiobjetivo basada en problemas
Este ejemplo muestra cómo resolver un problema de optimización multiobjetivo utilizando variables de optimización y cómo graficar la solución.
Formulación del problema
El problema tiene una variable de optimización bidimensional y dos funciones objetivo. Cree la variable de optimización x como un vector de fila, la orientación esperada por los solucionadores multiobjetivo. Establezca límites que especifiquen que los componentes de x van desde –50 hasta 50.
x = optimvar("x",1,2,LowerBound=-50,UpperBound=50);Crear la función objetivo de dos componentes. Incluir la función objetivo en un problema de optimización.
fun(1) = x(1)^4 + x(2)^4 + x(1)*x(2) - x(1)^2*x(2)^2 - 9*x(1)^2;
fun(2) = x(1)^4 + x(2)^4 + x(1)*x(2) - x(1)^2*x(2)^2 + 3*x(2)^3;
prob = optimproblem("Objective",fun);Revise el problema.
show(prob)
OptimizationProblem :
Solve for:
x
minimize :
((((x(1).^4 + x(2).^4) + (x(1) .* x(2))) - (x(1).^2 .* x(2).^2)) - (9 .* x(1).^2))
((((x(1).^4 + x(2).^4) + (x(1) .* x(2))) - (x(1).^2 .* x(2).^2)) + (3 .* x(2).^3))
variable bounds:
-50 <= x(1) <= 50
-50 <= x(2) <= 50
Resolver y representar la solución
Llame a solve para resolver el problema.
rng default % For reproducibility sol = solve(prob)
Solving problem using gamultiobj. gamultiobj stopped because the average change in the spread of Pareto solutions is less than options.FunctionTolerance.
sol =
1x18 OptimizationValues vector with properties:
Variables properties:
x: [2x18 double]
Objective properties:
Objective: [2x18 double]
Represente el frente de Pareto resultante.
paretoplot(sol)

Resuelva el problema nuevamente usando el solucionador paretosearch.
sol2 = solve(prob,Solver="paretosearch");Solving problem using paretosearch. Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
paretoplot(sol2)
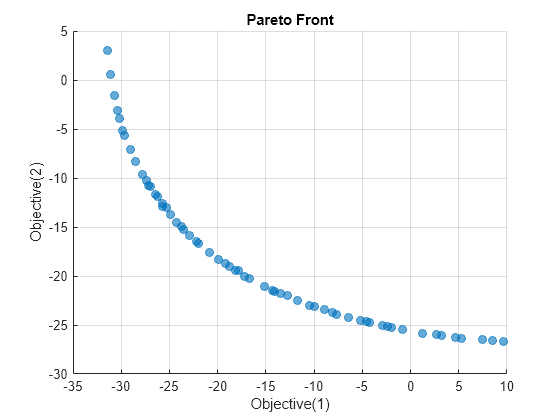
Utilizando las opciones predeterminadas, el solucionador paretosearch obtiene un conjunto más denso de puntos de solución que gamultiobj. Sin embargo, gamultiobj obtiene un rango más amplio de valores.
Partir de soluciones con un único objetivo
Para intentar lograr una mejor dispersión de soluciones, encuentre las soluciones de objetivo único a partir de x = [1 1].
x0.x = [1 1];
prob1 = optimproblem("Objective",fun(1));
solp1 = solve(prob1,x0);Solving problem using fmincon. Local minimum possible. Constraints satisfied. fmincon stopped because the size of the current step is less than the value of the step size tolerance and constraints are satisfied to within the value of the constraint tolerance.
prob2 = optimproblem("Objective",fun(2));
solp2 = solve(prob2,x0);Solving problem using fmincon. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance.
Prepare las soluciones de objetivo único como punto inicial para solve. Cada punto debe pasarse como un vector de columna a la función optimvalues.
start = optimvalues(prob,"x",[solp1.x' solp2.x']);Resuelva el problema multiobjetivo con paretosearch a partir de los puntos start.
sol3 = solve(prob,start,Solver="paretosearch");Solving problem using paretosearch. Pareto set found that satisfies the constraints. Optimization completed because the relative change in the volume of the Pareto set is less than 'options.ParetoSetChangeTolerance' and constraints are satisfied to within 'options.ConstraintTolerance'.
paretoplot(sol3)

Esta vez, paretosearch encuentra un rango más amplio de funciones objetivo, llegando casi a 10 en el Objetivo 2 y casi a 20 en el Objetivo 1. Este rango es similar al rango gamultiobj, excepto por el punto de solución anómalo cerca del Objetivo 1 = –31, Objetivo 2 = 48.
Consulte también
gamultiobj | paretosearch | solve | paretoplot