Flow Coefficient Parameterized Valve (TL)
Valve with flow area modeled in terms of its Cv or Kv flow coefficient
Libraries:
Simscape /
Fluids /
Thermal Liquid /
Valves & Orifices
Description
The Flow Coefficient Parameterized Valve (TL) block models the flow characteristics of a valve using the flow coefficient as a means to relate the flow rate through the ports to the pressure drop across them. The flow coefficient parameterization suits those cases in which the internal geometry of a valve is known in poor detail or in which the flow coefficient is the preferred means of characterizing a valve. The valve model is sufficiently general in its assumptions that it can be applied to a variety of valves; no single valve type is assumed in this block.
Flow Coefficient Parameterization
The flow coefficient measures the ease with which a fluid driven by a pressure differential flows across a valve. It is an important parameter in the sizing of valves and a convenient way of characterizing one in a model. In this role it is especially useful, as it quantifies in a single number all of the losses incurred in the flow passages of the valve. The flow coefficient is typically measured by the valve manufacturer and reported in a data sheet provided for the valve.
Strictly speaking there are two flow coefficients in common use: Cv and Kv. These describe what is fundamentally the same quantity: the volumetric flow rate of water passing through a valve that has been opened to its maximum and set to some standard operating conditions. The flow coefficients differ only in the temperature and pressure drop established during the measurement (the operating conditions) and in the physical units used in its expression:
Cv is measured at a generally accepted temperature of
60 °Fand pressure drop of1 PSI; it is expressed in imperial units ofUS gpm. This is the flow coefficient used in the model when the Flow coefficient specification block parameter is set toCv coefficient (USG/min)[1].Kv is measured at a generally accepted temperature of
15 °Cand pressure drop of1 bar; it is expressed in metric units ofm3/h. This is the flow coefficient used in the model when the Flow coefficient specification block parameter is set toKv coefficient (m^3/h). [2].
Two values are required of the flow coefficient, a maximum and a minimum. The maximum corresponds to a valve open to full capacity; this is the value frequently reported in valve data sheets. The minimum corresponds to a valve closed tight, when only leakage flow remains, if any at all. This lower bound imposed on the flow coefficient serves primarily to ensure the numerical robustness of the model. Its exact value is less important than its being a (generally very small) number greater than zero.
Valve Opening Parameterization
The opening fraction of the valve (the ratio of the valve opening area to its
maximum value) is determined during simulation from the input specified at port
L. This input is the control signal
and it is, in some valves, associated with stroke or
lift percent. The control signal can range in value from
0 to 1. If a lesser or greater value is
specified, it is adjusted to the nearest of the two limits. In other words, the
signal is saturated at 0 and
1.
The conversion from control signal to opening fraction depends on the
Valve opening characteristics parameterization selected in
the block. The calculation result is the same for all parameterizations when the
control signal is either 0 or 1: a value of
0 at port L always means a maximally
(though not necessarily completely) closed valve; a value of
1 always means a maximally open valve. At intermediate
values, the opening fractions differ:
Linear— The valve opening fraction (denoted f(L) in the figure) is equal to the control signal at port L. The two vary in tandem until the control signal either drops below zero (the valve is fully closed) or rises above its maximum value (the valve is fully open). The opening fraction ranges from0to1(a statement that does not apply to all valve opening parameterizations).
Quick opening— The valve opening fraction, f(L), is a power function of the control signal at port L. The opening fraction rises quickly with the control signal at values near0and slowly at values near1. The exponent (α) in the calculation determines how the opening rate changes with the control signal. The opening fraction ranges from0to1.
Equal percentage— The valve opening fraction is an exponential function of the control signal at port L. The opening fraction rises slowly with the control signal at values near0and quickly at values near1. The base of the exponent (R, the rangeability of the valve, the ratio between the maximum and minimum flow rates through the ports) determines how the opening rate changes with the control signal. The opening fraction ranges from a small fraction (0.02–0.05for typical rangeability values of20–50) to1.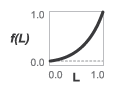
Mass Balance
The volume of fluid inside the valve, and therefore the mass of the same, is assumed to be very small and it is, for modeling purposes, ignored. As a result, no amount of fluid can accumulate there. By the principle of conservation of mass, the mass flow rate into the valve through one port must therefore equal that out of the valve through the other port:
where is defined as the mass flow rate into the valve through the port indicated by the subscript (A or B).
Momentum Balance
The causes of those pressure losses incurred in the passages of the valve are ignored in the block. Whatever their natures—sudden area changes, flow passage contortions—only their cumulative effect is considered during simulation. It is this cumulative effect that the flow coefficient of the valve enables the block to capture in a model. This constant factors in the momentum balance of the valve indirectly, by way of the effective opening area (S) of the same:
where:
p is the pressure at the port indicated by the subscript (A or B).
ρavg is the arithmetic mean of the fluid densities at the ports.
is the mass flow rate at a port.
is the critical mass flow rate, that at which the flow is assumed to switch between laminar and turbulent regimes:
where Recr is the Reynolds number at the transition point and μavg is the average of the dynamic viscosities at the ports.
The effective opening area (S) is the product of scaling of the maximum opening area of the valve by the opening fraction (f(L)). The calculation imposes a lower bound on the opening area at which only leakage flow remains:
where the subscripts max and
min refer to a valve in the fully opened and maximally closed
positions; the function f(L) is the opening fraction calculated from the control signal
specified at port L:
where α is obtained from the Exponent number block parameter and R from the Rangeability parameter. The maximum opening area is obtained by multiplying the (maximum) flow coefficient by an appropriate conversion factor:
where:
λC is the conversion factor between the maximum flow coefficient in imperial units (Cv,max) and the maximum opening area:
2.4015e-5 m^2.λK is the conversion factor between the maximum flow coefficient in SI units (Kv,max) and the maximum opening area:
2.7765e-5 m^2.
The minimum opening area in turn is obtained by multiplying the maximum opening area by the ratio between minimum and maximum flow coefficients:
Energy Balance
The valve is modeled as an adiabatic component. No heat exchange can occur between the fluid and the wall that surrounds it. No work is done on or by the fluid as it traverses from inlet to outlet. With these assumptions, energy can flow by advection only, through ports A and B. By the principle of conservation of energy, the sum of the port energy flows must then always equal zero:
where ϕ is defined as the energy flow rate into the valve through one of the ports (A or B).
Ports
Input
Conserving
Parameters
References
[1] Control Valve Handbook. 4th ed. Marshalltown, IA: Fisher Controls International. 2005.
[2] Flow of Fluids through Valves, Fittings and Pipe. Stamford, CT: Crane, 2010.
Extended Capabilities
Version History
Introduced in R2016a
