navfix
Mercator-based navigational fix
Syntax
[latfix,lonfix] = navfix(lat,long,az)
[latfix,lonfix] = navfix(lat,long,range,casetype)
[latfix,lonfix] = navfix(lat,long,az_range,casetype)
[latfix,lonfix] = navfix(lat,long,az_range,casetype,drlat,drlon)
Description
[latfix,lonfix] = navfix(lat,long,az) returns
the intersection points of rhumb lines drawn parallel to the observed
bearings, az, of the landmarks located at the points lat and long and
passing through these points. One bearing is required for each landmark.
Each possible pairing of the n landmarks generates one intersection,
so the total number of resulting intersection points is the combinatorial n
choose 2. The calculation time therefore grows rapidly
with n.
[latfix,lonfix] = navfix(lat,long,range,casetype) returns
the intersection points of Mercator projection circles with radii
defined by range, centered on the landmarks located
at the points lat and long.
One range value is required for each landmark. Each possible pairing
of the n landmarks generates up to two intersections
(circles can intersect twice), so the total number of resulting intersection
points is the combinatorial 2 times (n choose 2).
The calculation time therefore grows rapidly with n.
In this case, the variable casetype is a vector
of 0s the same size as the variable range.
[latfix,lonfix] = navfix(lat,long,az_range,casetype) combines
ranges and bearings. For each element of casetype equal
to 1, the corresponding element of az_range represents
an azimuth to the associated landmark. Where casetype is
a 0, az_range is a range.
[latfix,lonfix] = navfix(lat,long,az_range,casetype,drlat,drlon) returns
for each possible pairing of landmarks only the intersection that
lies closest to the dead reckoning position indicated by drlat and drlon.
When this syntax is used, all included landmarks' bearing lines or
range arcs must intersect. If any possible pairing fails, the warning No
Fix is displayed.
Background
This is a navigational function. It assumes that all latitudes and longitudes are in degrees and all distances are in nautical miles. In navigation, piloting is the practice of fixing one's position based on the observed bearing and ranges to fixed landmarks (points of land, lighthouses, smokestacks, etc.) from the navigator's vessel. In conformance with navigational practice, bearings are treated as rhumb lines and ranges are treated as the radii of circles on a Mercator projection.
In practice, at least three azimuths (bearings) and/or ranges are required for a usable fix. The resulting intersections are unlikely to coincide exactly.
Examples
Imagine you have two landmarks, at (15ºN,30.4ºW) and (14.8ºN,30.1ºW). You have a visual bearing to the first of 280º and to the second of 160º. Additionally, you have a range to the second of 12 nm. Find the intersection points:
[latfix,lonfix] = navfix([15 14.8 14.8],[-30.4 -30.1 -30.1],...
[280 160 12],[1 1 0])
latfix =
14.9591 NaN
14.9680 14.9208
14.9879 NaN
lonfix =
-30.1599 NaN
-30.2121 -29.9352
-30.1708 NaNHere is an illustration of the geometry:
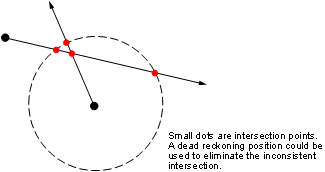
Limitations
Traditional plotting and the navfix function
are limited to relatively short distances. Visual bearings are in
fact great circle azimuths, not rhumb lines, and range arcs are actually
arcs of small circles, not of the planar circles plotted on the chart.
However, the mechanical ease of the process and the practical limits
of visual bearing ranges and navigational radar ranges (~30 nm) make
this limitation moot in practice. The error contributed because of
these assumptions is minuscule at that scale.
Tips
The outputs of this function are matrices providing the locations of the intersections for all possible pairings of the n entered lines of bearing and range arcs. These matrices therefore have n-choose-2 rows. In order to allow for two intersections per combination, these matrices have two columns. Whenever there are fewer than two intersections for that combination, one or two NaNs are returned in that row.
When a dead reckoning position is included, these matrices are column vectors.
Version History
Introduced before R2006a