Comparación gráfica de funciones exponenciales
Este ejemplo muestra un enfoque gráfico interesante para descubrir si es mayor que .
La pregunta es: ¿cuál es mayor, o ? Una forma fácil de averiguarlo es escribirlo directamente en la línea de comandos de MATLAB®. Sin embargo, otra manera de analizar la situación es hacer una pregunta más general: ¿qué forma tiene la función ?
A continuación, se muestra una gráfica de .
% Define the mesh x = 0:0.16:5; y = 0:0.16:5; [xx,yy] = meshgrid(x,y); % The plot zz = xx.^yy-yy.^xx; h = surf(x,y,zz); h.EdgeColor = [0.7 0.7 0.7]; view(20,50); colormap(hsv); title('$z = x^y-y^x$','Interpreter','latex') xlabel('x') ylabel('y') hold on
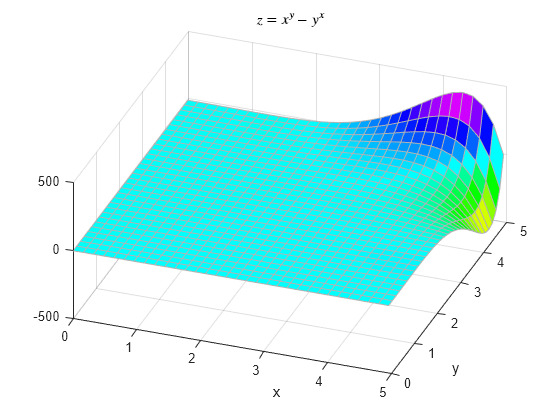
La solución de la ecuación presenta una forma muy interesante y nuestra pregunta original no se resuelve fácilmente mediante observación. A continuación, se muestra una gráfica de los valores xy, que ofrecen un resultado de .
c = contourc(x,y,zz,[0 0]); list1Len = c(2,1); xContour = [c(1,2:1+list1Len) NaN c(1,3+list1Len:size(c,2))]; yContour = [c(2,2:1+list1Len) NaN c(2,3+list1Len:size(c,2))]; % Note that the NAN above prevents the end of the first contour line from being % connected to the beginning of the second line line(xContour,yContour,'Color','k');

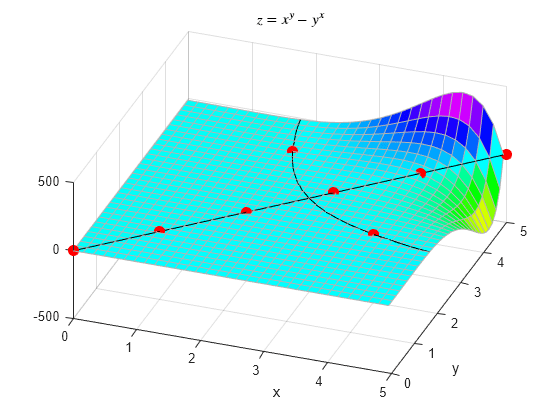
Algunas combinaciones de x e y a lo largo de la curva de color negro son números enteros. La siguiente gráfica muestra las soluciones en números enteros a la ecuación . Observe que es la única solución en números enteros en la que .
plot([0:5 2 4],[0:5 4 2],'r.','MarkerSize',25);
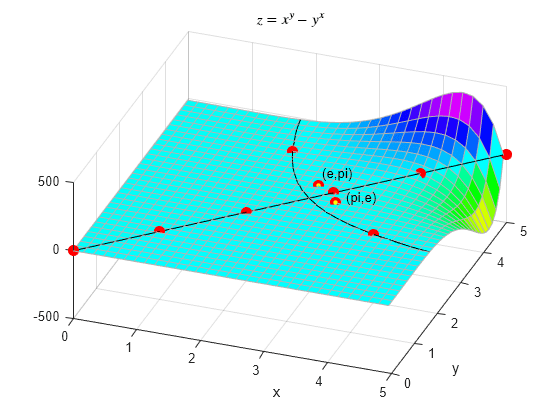
Finalmente, represente los puntos y en la superficie. El resultado muestra que es efectivamente mayor que (aunque no por mucho).
e = exp(1); plot([e pi],[pi e],'r.','MarkerSize',25); plot([e pi],[pi e],'y.','MarkerSize',10); text(e,3.3,'(e,pi)','Color','k', ... 'HorizontalAlignment','left','VerticalAlignment','bottom'); text(3.3,e,'(pi,e)','Color','k','HorizontalAlignment','left',... 'VerticalAlignment','bottom'); hold off;
Compruebe los resultados.
e = exp(1); e^pi
ans = 23.1407
pi^e
ans = 22.4592