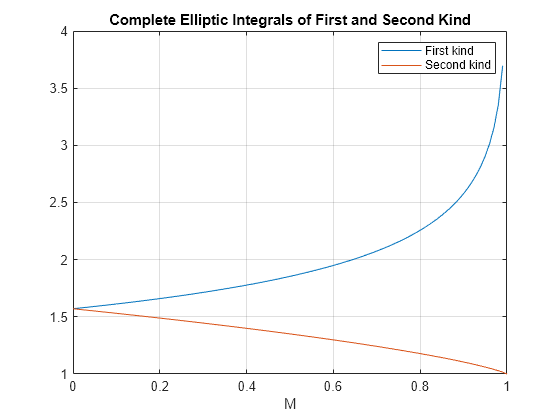
ellipke
Complete elliptic integrals of first and second kind
Description
Examples
Input Arguments
Output Arguments
More About
References
[1] Abramowitz, M., and I. A. Stegun. Handbook of Mathematical Functions. Dover Publications, 1965.
Extended Capabilities
Version History
Introduced before R2006a