Problema del viajante: Basado en solvers
Este ejemplo muestra cómo utilizar programación de enteros binaria para resolver el problema clásico del viajante. Este problema implica encontrar el trayecto (ruta) cerrado más corto pasando por un conjunto de paradas (ciudades). En este caso hay 200 paradas, pero puede cambiar fácilmente la variable nStops para obtener un tamaño de problema diferente. Resolverá el problema inicial y verá que la solución tiene subtrayectos. Esto significa que la solución óptima encontrada no proporciona una ruta continua por todos los puntos, sino que tiene varios bucles desconectados. Después utilizará un proceso iterativo para determinar los subtrayectos, añadiendo restricciones y volviendo a ejecutar la optimización hasta que los subtrayectos se eliminen.
Para el enfoque basado en problemas, consulte Problema del viajante: Basado en problemas.
Formulación del problema
Formule el problema del viajante para programación lineal de enteros de la siguiente forma:
Genere todos los viajes posibles, es decir, todas las parejas de paradas diferentes.
Calcule la distancia para cada viaje.
La función de coste que se desea minimizar es la suma de las distancias del viaje para cada viaje del trayecto.
Las variables de decisión son binarias y están asociadas a cada viaje, donde cada 1 representa un viaje que existe en el trayecto y cada 0 representa un viaje que no está en el trayecto.
Para garantizar que el trayecto incluya todas las paradas, añada la restricción lineal de que cada parada esté exactamente entre dos viajes. Esto implica una llegada y una salida en cada parada.
Generar paradas
Genere paradas aleatorias dentro de una representación poligonal en bruto de los EE. UU. continentales.
load('usborder.mat','x','y','xx','yy'); rng(3,'twister') % Makes a plot with stops in Maine & Florida, and is reproducible nStops = 200; % You can use any number, but the problem size scales as N^2 stopsLon = zeros(nStops,1); % Allocate x-coordinates of nStops stopsLat = stopsLon; % Allocate y-coordinates n = 1; while (n <= nStops) xp = rand*1.5; yp = rand; if inpolygon(xp,yp,x,y) % Test if inside the border stopsLon(n) = xp; stopsLat(n) = yp; n = n+1; end end
Calcular distancias entre puntos
Dado que existen 200 paradas, hay 19.900 viajes, es decir, 19.900 variables binarias (# variables = 200 elegir 2).
Genere todos los viajes, es decir, todas las parejas de paradas.
idxs = nchoosek(1:nStops,2);
Calcule todas las distancias de los viajes, asumiendo que la tierra es plana para utilizar el teorema de Pitágoras.
dist = hypot(stopsLat(idxs(:,1)) - stopsLat(idxs(:,2)), ...
stopsLon(idxs(:,1)) - stopsLon(idxs(:,2)));
lendist = length(dist);Con esta definición del vector dist, la longitud de un trayecto es
dist'*x_tsp
donde x_tsp es el vector de solución binario. Esta es la distancia de un trayecto que se intenta minimizar.
Crear una gráfica y diseñar un mapa
Represente el problema como una gráfica. Cree una gráfica donde todas las paradas sean nodos y los viajes sean bordes.
G = graph(idxs(:,1),idxs(:,2));
Muestre las paradas utilizando una gráfica. Represente los nodos sin los bordes de la gráfica.
figure hGraph = plot(G,'XData',stopsLon,'YData',stopsLat,'LineStyle','none','NodeLabel',{}); hold on % Draw the outside border plot(x,y,'r-') hold off

Restricciones
Cree las restricciones lineales de que cada parada tenga dos viajes asociados, ya que debe haber un viaje hasta cada parada y un viaje desde cada parada.
Aeq = spalloc(nStops,length(idxs),nStops*(nStops-1)); % Allocate a sparse matrix for ii = 1:nStops whichIdxs = (idxs == ii); % Find the trips that include stop ii whichIdxs = sparse(sum(whichIdxs,2)); % Include trips where ii is at either end Aeq(ii,:) = whichIdxs'; % Include in the constraint matrix end beq = 2*ones(nStops,1);
Límites binarios
Todas las variables de decisión son binarias. Establezca el argumento intcon en el número de variables de decisión y ponga un límite inferior de 0 y un límite superior de 1 en cada una.
intcon = 1:lendist; lb = zeros(lendist,1); ub = ones(lendist,1);
Optimizar utilizando intlinprog
El problema está listo para su resolución. Para suprimir la salida iterativa, desactive la visualización predeterminada.
opts = optimoptions('intlinprog','Display','off'); [x_tsp,costopt,exitflag,output] = intlinprog(dist,intcon,[],[],Aeq,beq,lb,ub,opts);
Cree una nueva gráfica con los viajes de la solución como bordes. Para hacerlo, redondee la solución en caso de que algunos valores no sean exactamente enteros, y convierta los valores resultantes a logical.
x_tsp = logical(round(x_tsp));
Gsol = graph(idxs(x_tsp,1),idxs(x_tsp,2),[],numnodes(G));
% Gsol = graph(idxs(x_tsp,1),idxs(x_tsp,2)); % Also works in most casesVisualizar la solución
hold on highlight(hGraph,Gsol,'LineStyle','-') title('Solution with Subtours')

Como puede verse en el mapa, la solución tiene varios subtrayectos. Las restricciones especificadas hasta ahora no evitan estos subtrayectos. Para evitar cualquier posible subtrayecto, necesitaría un número increíblemente amplio de restricciones de desigualdad.
Restricciones de subtrayecto
Dado que no se pueden añadir todas las restricciones de subtrayecto, adopte un enfoque iterativo. Detecte los subtrayectos en la solución actual y, después, añada restricciones de desigualdad para evitar esos subtrayectos en particular. Al hacerlo, se encuentra un trayecto adecuado en unas pocas iteraciones.
Elimine los subtrayectos con restricciones de desigualdad. Un ejemplo de cómo funciona es que, si tiene cinco puntos en un subtrayecto, tendrá cinco líneas conectando estos puntos para crear el subtrayecto. Elimine este subtrayecto implementando una restricción de desigualdad que diga que debe haber cuatro líneas o menos entre estos cinco puntos.
Aún mejor, encuentre todas las líneas entre estos cinco puntos y restrinja la solución para que no tenga más de cuatro de estas líneas. Se trata de una restricción correcta porque, si en una solución existen cinco o más líneas, la solución tendría un subtrayecto (una gráfica con nodos y bordes siempre contiene un ciclo).
Detecte el subtrayecto identificando los componentes conectados en Gsol, la gráfica creada con los bordes en la solución actual. conncomp devuelve un vector con el número del subtrayecto al que pertenece cada borde.
tourIdxs = conncomp(Gsol); numtours = max(tourIdxs); % number of subtours fprintf('# of subtours: %d\n',numtours);
# of subtours: 27
Incluya las restricciones de desigualdad lineales para eliminar subtrayectos y llame repetidamente al solver hasta que solo quede un subtrayecto.
A = spalloc(0,lendist,0); % Allocate a sparse linear inequality constraint matrix b = []; while numtours > 1 % Repeat until there is just one subtour % Add the subtour constraints b = [b;zeros(numtours,1)]; % allocate b A = [A;spalloc(numtours,lendist,nStops)]; % A guess at how many nonzeros to allocate for ii = 1:numtours rowIdx = size(A,1) + 1; % Counter for indexing subTourIdx = find(tourIdxs == ii); % Extract the current subtour % The next lines find all of the variables associated with the % particular subtour, then add an inequality constraint to prohibit % that subtour and all subtours that use those stops. variations = nchoosek(1:length(subTourIdx),2); for jj = 1:length(variations) whichVar = (sum(idxs==subTourIdx(variations(jj,1)),2)) & ... (sum(idxs==subTourIdx(variations(jj,2)),2)); A(rowIdx,whichVar) = 1; end b(rowIdx) = length(subTourIdx) - 1; % One less trip than subtour stops end % Try to optimize again [x_tsp,costopt,exitflag,output] = intlinprog(dist,intcon,A,b,Aeq,beq,lb,ub,opts); x_tsp = logical(round(x_tsp)); Gsol = graph(idxs(x_tsp,1),idxs(x_tsp,2),[],numnodes(G)); % Gsol = graph(idxs(x_tsp,1),idxs(x_tsp,2)); % Also works in most cases % Visualize result hGraph.LineStyle = 'none'; % Remove the previous highlighted path highlight(hGraph,Gsol,'LineStyle','-') drawnow % How many subtours this time? tourIdxs = conncomp(Gsol); numtours = max(tourIdxs); % number of subtours fprintf('# of subtours: %d\n',numtours) end
# of subtours: 20 # of subtours: 7 # of subtours: 9 # of subtours: 9 # of subtours: 3 # of subtours: 2 # of subtours: 7 # of subtours: 2 # of subtours: 1
title('Solution with Subtours Eliminated'); hold off
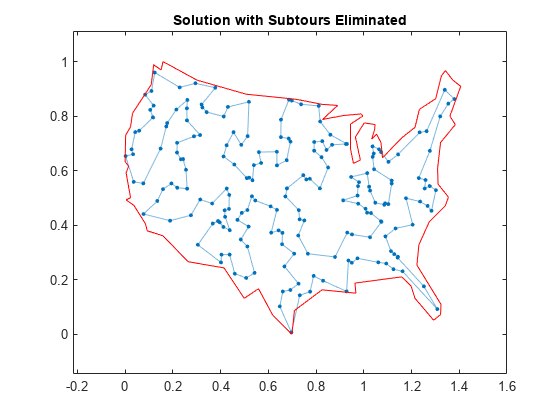
Calidad de la solución
La solución representa un trayecto factible porque se trata de un bucle cerrado único. Pero, ¿se trata de un trayecto con coste mínimo? Una forma de descubrirlo es examinar la estructura de salida.
disp(output.absolutegap)
1.8300e-04
El tamaño pequeño del intervalo absoluto implica que la solución es óptima o tiene una longitud total casi óptima.