2-D Field Solver
The 2-D field solver in RF PCB Toolbox™ allows you to model and analyze the
cross-sections of multi-conductor transmission lines in a multi-layered dielectric above
a ground plane like a microstrip line. See microstripLine. For more detailed information, see [1]
The four primary transmission line parameters are the resistance R, the inductance L, the conductance G and the capacitance C. You can obtain these parameters by applying a total charge on the conductor-to-dielectric interfaces and a polarization charge on the dielectric-to-dielectric interfaces and solving the electrostatic field created. The 2D field solver uses pulse approximation for the total charge σT and discretizes the contours of the conductor-to-dielectric and dielectric-to-dielectric interfaces using straight line segments. The density of the segments are controlled by the distribution of nodes along these contours. The figure shows the discretization for a single conductor transmission line in a single layered dielectric above a ground plane.
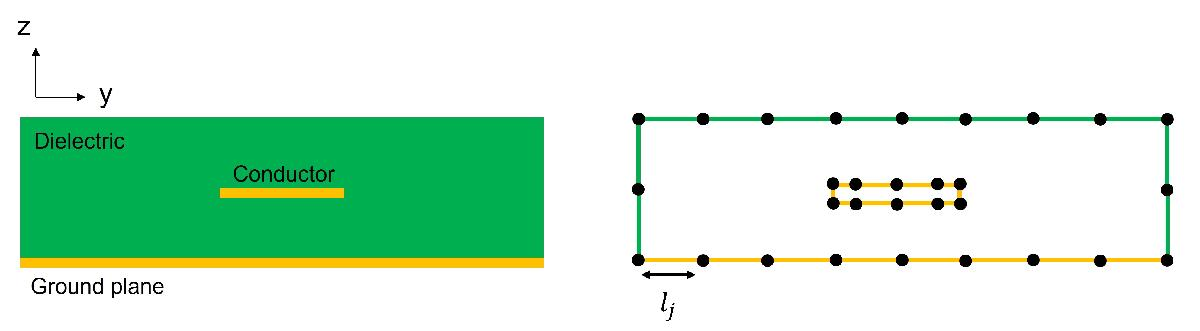
At any point p in the YZ plane and above the ground plane, the potential ϕ is due to the combination of σT
and the image of σT about the ground plane. J represents the conductor and layers in the PCB, where J = J1 + + J2. J1 is the number of conductor-to-dielectric interfaces and J2 is the number of dielectric-to-dielectric interfaces.
where lj is the contour of jth interface in the Y-Z plane, dl' is the differential element of length at p' on lj and is the image of p' about the ground plane.
The electric field is given by ϕ. Substituting ϕ into this equation yields
The normal component of a displacement field is continuous across dielectric-to-dielectric interface. You can derive the second integral equation by substituting the formula for Ep into the interface conditions for displacement fields. You can solve the set of integral equations for a total charge σT using the methods of moments [2]. The analysis includes skin-effect, conductor losses, and dielectric losses.
References
[1] Djordjevis, Antonije R., Miodrag B. Bazdar, Tapan K. Sarkar and Roger F. Harrington, Linpar for Windows: Matrix Parameters for Multiconductor Transmission Lines. Artech House, 1999
[2] Harringhton, R. F. Field Computation by Moment Methods. New York, Macmillan, 1968