Análisis de cepstrum
¿Qué es un cepstrum?
El análisis de cepstrum es una técnica de procesamiento de señales no lineales con una serie de aplicaciones en ámbitos como el procesamiento de imagen y voz.
El cepstrum complejo de una secuencia x se calcula encontrando el logaritmo natural complejo de la transformada de Fourier de x y, después, la transformada de Fourier inversa de la secuencia resultante:
La función cceps de la toolbox realiza esta operación y estima el cepstrum complejo de una secuencia de entrada. Devuelve una secuencia real del mismo tamaño que la secuencia de entrada.
Puede utilizar la función cceps en una aplicación de detección de eco. Primero, cree una onda sinusoidal de 45 Hz muestreada a 100 Hz. Añada un eco de la señal, con la mitad de la amplitud, 0,2 segundos después del comienzo de la señal.
t = 0:0.01:1.27; s1 = sin(2*pi*45*t); s2 = s1 + 0.5*[zeros(1,20) s1(1:108)];
Calcule y represente el cepstrum complejo de la señal nueva.
c = cceps(s2); plot(t,c)
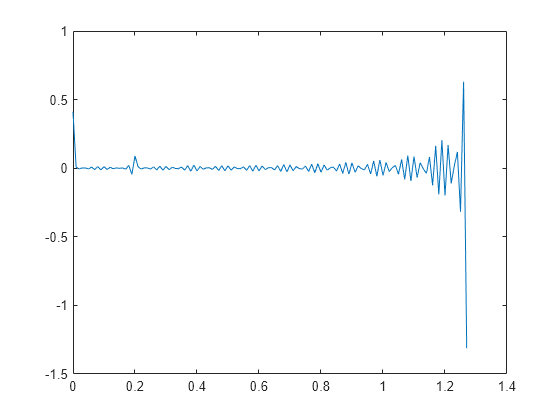
El cepstrum complejo muestra un pico a 0,2 segundos que indica el eco.
El cepstrum real de una señal x, en ocasiones llamado simplemente cepstrum, se calcula determinando el logaritmo natural de magnitud de la transformada de Fourier de x y, después, obteniendo la transformada de Fourier inversa de la secuencia resultante:
La función rceps de la toolbox realiza esta operación y devuelve el cepstrum real de una secuencia. La secuencia devuelta es un vector de valor real del mismo tamaño que el vector de entrada.
La función rceps también devuelve una secuencia de fase mínima única que tiene el mismo cepstrum real que la entrada. Para obtener tanto el cepstrum real como la reconstrucción de fase mínima de una secuencia, utilice [y,ym] = rceps(x), donde y es el cepstrum real y ym es la reconstrucción de fase mínima de x. El ejemplo siguiente muestra que una salida de rceps es una secuencia de fase mínima única con el mismo cepstrum real que x.
y = [4 1 5]; % Non-minimum phase sequence
[xhat,yhat] = rceps(y);
xhat2 = rceps(yhat);
[xhat' xhat2']ans = 3×2
1.6225 1.6225
0.3400 0.3400
0.3400 0.3400
Cepstrum complejo inverso
Para invertir el cepstrum complejo, utilice la función icceps. La inversión es complicada por el hecho de que la función cceps realiza una modificación de fase dependiente de datos, de forma que la fase no envuelta de su entrada es continua a frecuencia cero. La modificación de fase es equivalente a un retardo de un entero. cceps devuelve este término de retardo si solicita una segunda salida:
x = 1:10; [xhat,delay] = cceps(x)
xhat = 1×10
2.2428 -0.0420 -0.0210 0.0045 0.0366 0.0788 0.1386 0.2327 0.4114 0.9249
delay = 1
Para invertir el cepstrum complejo, utilice icceps con el parámetro de retardo original:
icc = icceps(xhat,2)
icc = 1×10
2.0000 3.0000 4.0000 5.0000 6.0000 7.0000 8.0000 9.0000 10.0000 1.0000
Tal y como se muestra en el ejemplo anterior, el término de retardo original puede dejar de ser válido si se modifica de cualquier forma el cepstrum complejo. No podrá invertir el cepstrum complejo de forma exacta.