constructDefaultFixedEffectValues
Create structure containing initial estimates fixed effects needed for fit
Description
FEInitEstimates = constructDefaultFixedEffectValues(CovModel)FEInitEstimates, a structure containing the initial estimates
for the fixed effects in CovModel, a CovariateModel
object. By default, the values of initial estimates are set to zero.
Examples
Create an empty CovariateModel object.
covModel = CovariateModel;
Set its Expression property to define the relationships between parameters (Cl, V, and k) and covariate (w). You must use theta as a prefix for all fixed effects and eta for random effects.
covModel.Expression = ["Cl = theta1 + theta2*w + eta1","V = theta3 + eta2","k = theta4 + eta3"];
Display the names of fixed effects.
covModel.FixedEffectNames
ans = 4×1 cell
{'theta1'}
{'theta3'}
{'theta4'}
{'theta2'}
The FixedEffectDescription property displays which fixed effects correspond to which parameter. For instance, theta1 is the fixed effect for the Cl parameter, and theta2 is the fixed effect for the weight covariate that has a correlation with Cl parameter, denoted as Cl/w.
covModel.FixedEffectDescription
ans = 4×1 cell
{'Cl' }
{'V' }
{'k' }
{'Cl/w'}
Specify initial estimates for the fixed effects. Create a default structure containing initial estimates using the constructDefaultFixedEffectValues function.
initialEstimates = constructDefaultFixedEffectValues(covModel)
initialEstimates = struct with fields:
theta1: 0
theta3: 0
theta4: 0
theta2: 0
Update the initial estimate value of each fixed effects.
initialEstimates.theta1 = 1.20; initialEstimates.theta2 = 0.30; initialEstimates.theta3 = 0.90; initialEstimates.theta4 = 0.10;
Update the FixedEffectValues property to use the updated initial estimates.
covModel.FixedEffectValues = initialEstimates;
Check the covariate model for errors.
verify(covModel)
Estimate nonlinear mixed-effects parameters using clinical pharmacokinetic data collected from 59 infants. Evaluate the fitted model given new data or dosing information.
Load Data
This example uses data collected on 59 preterm infants given phenobarbital during the first 16 days after birth [1]. ds is a table containing the concentration-time profile data and covariate information for each infant (or group).
load pheno.mat ds
Convert to groupedData
Convert the data to the groupedData format for parameter estimation.
data = groupedData(ds);
Display the first few rows of data.
data(1:5,:)
ans =
5×6 groupedData
ID TIME DOSE WEIGHT APGAR CONC
__ ____ ____ ______ _____ ____
1 0 25 1.4 7 NaN
1 2 NaN 1.4 7 17.3
1 12.5 3.5 1.4 7 NaN
1 24.5 3.5 1.4 7 NaN
1 37 3.5 1.4 7 NaN
Visualize Data
Display the data in a trellis plot.
t = sbiotrellis(data, 'ID', 'TIME', 'CONC', 'marker', 'o',... 'markerfacecolor', [.7 .7 .7], 'markeredgecolor', 'r', ... 'linestyle', 'none'); t.plottitle = 'Concentration versus Time';
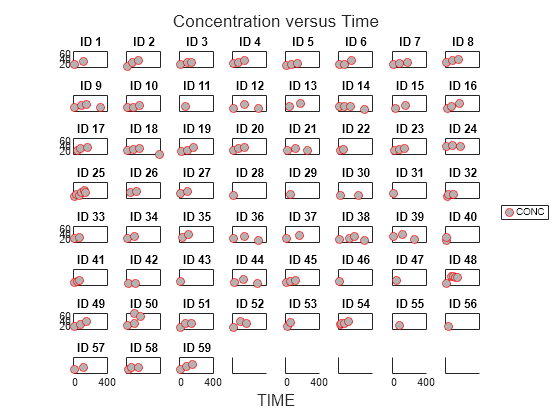
Create a One-Compartment PK Model
Create a simple one-compartment PK model, with bolus dose administration and linear clearance elimination, to fit the data.
pkmd = PKModelDesign; addCompartment(pkmd,'Central','DosingType','Bolus',... 'EliminationType','linear-clearance',... 'HasResponseVariable',true,'HasLag',false); onecomp = pkmd.construct;
Map model species to response data.
responseMap = 'Drug_Central = CONC';Define Estimated Parameters
The parameters to estimate in this model are the volume of the central compartment (Central) and the clearance rate (Cl_Central). sbiofitmixed calculates fixed and random effects for each parameter. The underlying algorithm computes normally distributed random effects, which might violate constraints for biological parameters that are always positive, such as volume and clearance. Therefore, specify a transform for the estimated parameters so that the transformed parameters follow a normal distribution. The resulting model is
and
where , , and are the fixed effects, random effects, and estimated parameter values respectively, calculated for each infant (group) . Some arbitrary initial estimates for V (volume of central compartment) and Cl (clearance rate) are used here in the absence of better empirical data.
estimatedParams = estimatedInfo({'log(Central)','log(Cl_Central)'},'InitialValue',[1 1]);Define Dosing
All infants were given the drug, represented by the Drug_Central species, where the dosing schedule varies among infants. The amount of drug is listed in the data variable DOSE. You can automatically generate dose objects from the data and use them during fitting. In this example, Drug_Central is the target species that receives the dose.
sampleDose = sbiodose('sample','TargetName','Drug_Central'); doses = createDoses(data,'DOSE','',sampleDose);
Fit the Model
Use sbiofitmixed to fit the one-compartment model to the data.
nlmeResults = sbiofitmixed(onecomp,data,responseMap,estimatedParams,doses,'nlmefit');Visualize Results
Visualize the fitted results using individual-specific parameter estimates.
plot(nlmeResults,'ParameterType','individual');
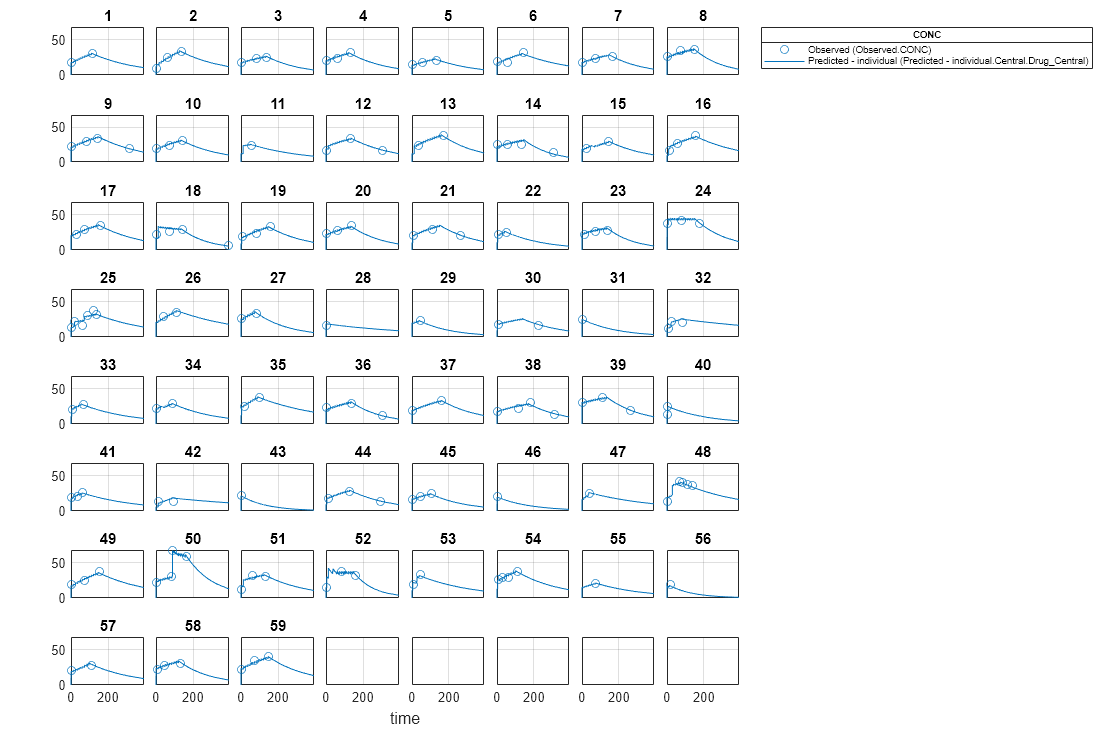
Use New Dosing Data to Simulate the Fitted Model
Suppose you want to predict how infants 1 and 2 would have responded under different dosing amounts. You can predict their responses as follows.
Create new dose objects with new dose amounts.
dose1 = doses(1); dose1.Amount = dose1.Amount*2; dose2 = doses(2); dose2.Amount = dose2.Amount*1.5;
Use the predict function to evaluate the fitted model using the new dosing data. If you want response predictions at particular times, provide the new output time vector. Use the 'ParameterType' option to specify individual or population parameters to use. By default, predict uses the population parameters when you specify output times.
timeVec = [0:25:400]; newResults = predict(nlmeResults,timeVec,[dose1;dose2],'ParameterType','population');
Visualize the predicted responses while overlapping the experimental data for infants 1 and 2.
figure; subplot(2,1,1) plot(data.TIME(data.ID == 1),data.CONC(data.ID == 1),'bo') hold on plot(newResults(1).Time,newResults(1).Data,'b') hold off ylabel('Concentration') legend('Observation(CONC)','Prediction') subplot(2,1,2) plot(data.TIME(data.ID == 2),data.CONC(data.ID == 2),'rx') hold on plot(newResults(2).Time,newResults(2).Data,'r') hold off legend('Observation(CONC)','Prediction') ylabel('Concentration') xlabel('Time')
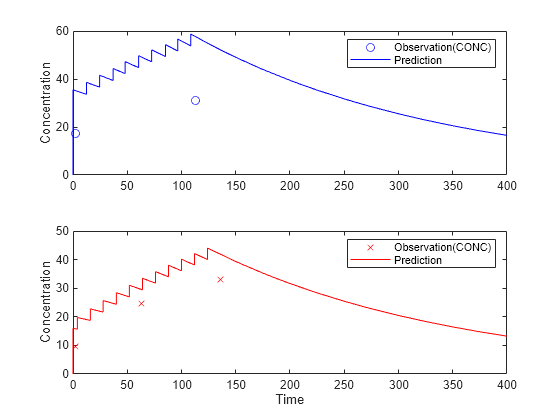
Create a Covariate Model for the Covariate Dependencies
Suppose there is a correlation between volume and weight, and possibly volume and APGAR score. Consider the effect of weight by modeling two of these covariate dependencies: the volume of central (Central) and the clearance rate (Cl_Central) vary with weight. The model becomes
and
Use the CovariateModel object to define the covariate dependencies. For details, see Specify a Covariate Model.
covModel = CovariateModel;
covModel.Expression = ({'Central = exp(theta1 + theta2*WEIGHT + eta1)',...
'Cl_Central = exp(theta3 + theta4*WEIGHT + eta2)'});Use constructDefaultInitialEstimate to create an initialEstimates struct.
initialEstimates = covModel.constructDefaultFixedEffectValues;
Use the FixedEffectNames property to display the thetas (fixed effects) defined in the model.
covModel.FixedEffectNames
ans = 4×1 cell
{'theta1'}
{'theta3'}
{'theta2'}
{'theta4'}
Use the FixedEffectDescription property to show the descriptions of corresponding fixed effects (thetas) used in the covariate expression. For example, theta2 is the fixed effect for the weight covariate that correlates with the volume (Central), denoted as 'Central/WEIGHT'.
disp('Fixed Effects Description:');Fixed Effects Description:
disp(covModel.FixedEffectDescription);
{'Central' }
{'Cl_Central' }
{'Central/WEIGHT' }
{'Cl_Central/WEIGHT'}
Set the initial guesses for the fixed-effect parameter values for Central and Cl_Central using the values estimated from fitting the base model.
initialEstimates.theta1 = nlmeResults.FixedEffects.Estimate(1); initialEstimates.theta3 = nlmeResults.FixedEffects.Estimate(2); covModel.FixedEffectValues = initialEstimates;
Fit the Model
nlmeResults_cov = sbiofitmixed(onecomp,data,responseMap,covModel,doses,'nlmefit');Display Fitted Parameters and Covariances
disp('Estimated Fixed Effects:');Estimated Fixed Effects:
disp(nlmeResults_cov.FixedEffects);
Name Description Estimate StandardError
__________ _____________________ ________ _____________
{'theta1'} {'Central' } -0.45664 0.078933
{'theta3'} {'Cl_Central' } -5.9519 0.1177
{'theta2'} {'Central/WEIGHT' } 0.52948 0.047342
{'theta4'} {'Cl_Central/WEIGHT'} 0.61954 0.071386
disp('Estimated Covariance Matrix:');Estimated Covariance Matrix:
disp(nlmeResults_cov.RandomEffectCovarianceMatrix);
eta1 eta2
________ ________
eta1 0.046503 0
eta2 0 0.041609
Visualize Results
Visualize the fitted results using individual-specific parameter estimates.
plot(nlmeResults_cov,'ParameterType','individual');

Use New Covariate Data to Evaluate the Fitted Model
Suppose you want to explore the responses of infants 1 and 2 using different covariate data, namely WEIGHT. You can do this by specifying the new WEIGHT data. The ID variable of the data corresponds to individual infants.
newData = data(data.ID == 1 | data.ID == 2,:); newData.WEIGHT(newData.ID == 1) = 1.3; newData.WEIGHT(newData.ID == 2) = 1.4;
Simulate the responses of infants 1 and 2 using the new covariate data.
[newResults_cov, newEstimates] = predict(nlmeResults_cov,newData,[dose1;dose2]);
newEstimates contains the updated parameter estimates for each individual (infants 1 and 2) after the model is reevaluated using the new covariate data.
newEstimates
newEstimates=4×3 table
Group Name Estimate
_____ ______________ _________
1 {'Central' } 2.5596
1 {'Cl_Central'} 0.0065965
2 {'Central' } 1.7123
2 {'Cl_Central'} 0.0064806
Compare to the estimated values from the original fit using the old covariate data.
nlmeResults_cov.IndividualParameterEstimates( ... nlmeResults_cov.IndividualParameterEstimates.Group == '1' | ... nlmeResults_cov.IndividualParameterEstimates.Group == '2',:)
ans=4×3 table
Group Name Estimate
_____ ______________ _________
1 {'Central' } 2.6988
1 {'Cl_Central'} 0.0070181
2 {'Central' } 1.8054
2 {'Cl_Central'} 0.0068948
Visualize the new simulation results together with the experimental data for infant 1 and 2.
figure; subplot(2,1,1); plot(data.TIME(data.ID == 1),data.CONC(data.ID == 1),'bo') hold on plot(newResults_cov(1).Time,newResults_cov(1).Data,'b') hold off ylabel('Concentration') legend('Observation(CONC)','Prediction','Location','NorthEastOutside') subplot(2,1,2) plot(data.TIME(data.ID == 2),data.CONC(data.ID == 2),'rx') hold on plot(newResults_cov(2).Time,newResults_cov(2).Data,'r') hold off legend('Observation(CONC)','Prediction','Location','NorthEastOutside') ylabel('Concentration') xlabel('Time')

References
[1] Grasela, T. H. Jr., and S. M. Donn. "Neonatal population pharmacokinetics of phenobarbital derived from routine clinical data." Dev Pharmacol Ther 1985:8(6). 374-83.
Input Arguments
Covariate model, specified as a CovariateModel object.
Output Arguments
Initial estimates for fixed effects, returned as a structure. Each field of the
structure represents a fixed effect and its value. By default, the values of initial
estimates are set to zero, but you can edit these estimates as needed. If you do, make
sure that the number and names of the fields in the FEInitEstimates
structure matches the number and names of fixed effects (theta
values) in the Expression property of
CovModel.
Version History
Introduced in R2011b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)