Tune PID Controller for Mass-Spring-Damper System Using Virtual Reference Feedback Tuning Block

Since R2025a

This example shows how to use the Virtual Reference Feedback Tuning (VRFT) block to tune PID controller for a mass-spring-damper system. The example demonstrates using input and output data sequences while simulating a mass-spring-damper plant model in a closed-loop configuration.

Mass-Spring-Damper Plant Model

The mass-spring-damper system consists of two carts of mass ${\mathit{m}}_1$ and ${\mathit{m}}_2$, connected to each other and ground through both springs and dampers. The springs are with stiffness coefficients ${\mathit{k}}_1$and ${\mathit{k}}_2$. The dampers are with damping coefficients ${\mathit{c}}_1$ and ${\mathit{c}}_2$.

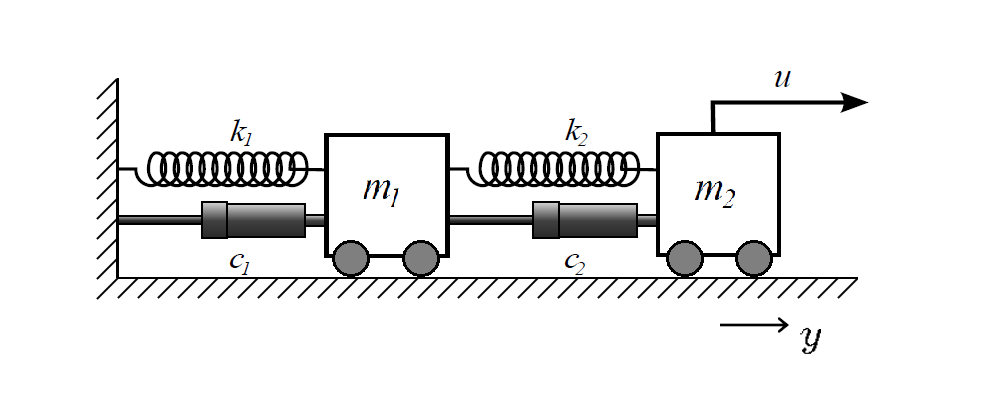
Define the model parameters.

m1 = 1;
m2 = 0.5;
c1 = 0.2;
c2 = 0.5;
k1 = 1;
k2 = 0.5;

Using the parameters, you can define an LTI system plant model for the mass-spring-damper system.

sys_tf = tf([m1 c1+c2 k1+k2],[m1*m2 m2*(c1+c2)+m1*c2 m2*(k1+k2)+m1*k2+c1*c2 c1*k2+k1*c2 k1*k2]);

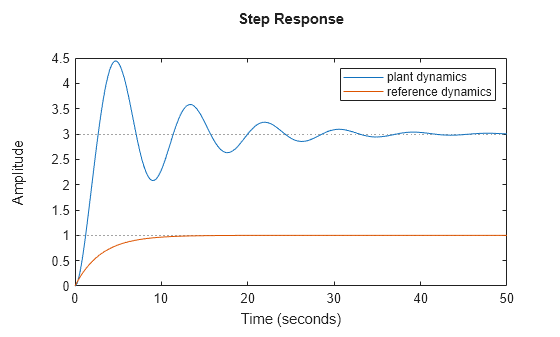
In the VRFT block settings, the reference model captures the desired closed-loop behavior with tuned PID controllers. In this example, the reference model is a continuous-time first-order linear system, expressed as a transfer function of tf(1,[3 1]). The following plot shows the different step responses between the open-loop plant dynamics and the desired closed-loop behavior.

figure;
step(sys_tf,tf(1,[3 1]))
legend('plant dynamics','reference dynamics')

The VRFT block is a discrete-time block. Define its sample time the same as the PID controller block.

Ts = 0.1;

Closed-Loop Simulink Model

Open the Simulink® model that includes an LTI plant model object. This model includes an initial PID controller that regulates the output. The goal is to use the VRFT block to tune the PID controller parameters and achieve a closed-loop response that is close to the reference linear system tf(1,[3 1]).

mdl = "ClosedLoopTuningOfPIDControllerUsingVRFT";
open_system(mdl);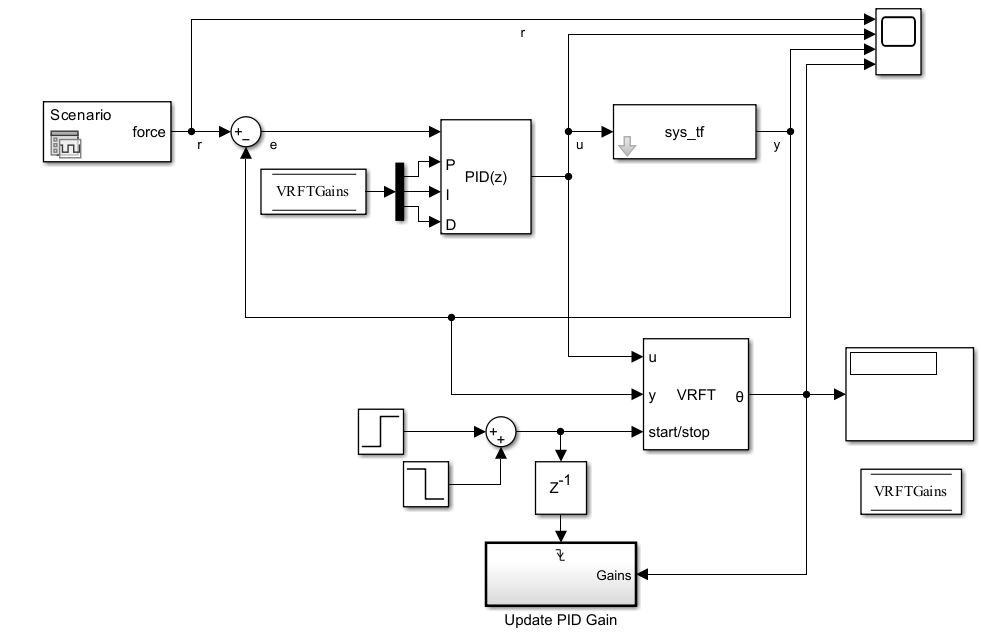

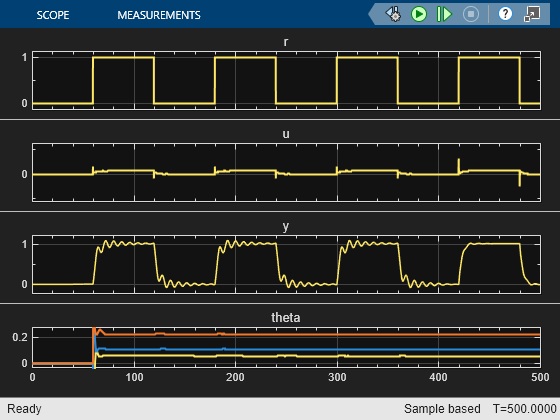
The block tunes the PID controller gains during the experiment period, which is controlled by the start-stop signal constructed using step signals. For instance, the model uses a start/stop signal from t = 1 s to 400 s. The model updates the tuned PID controller gains directly at the end of the tuning period. Simulate the model and observe that the response improves after the tuning process finishes and tuned PID controller parameters are applied automatically.

SimOut = sim(mdl);

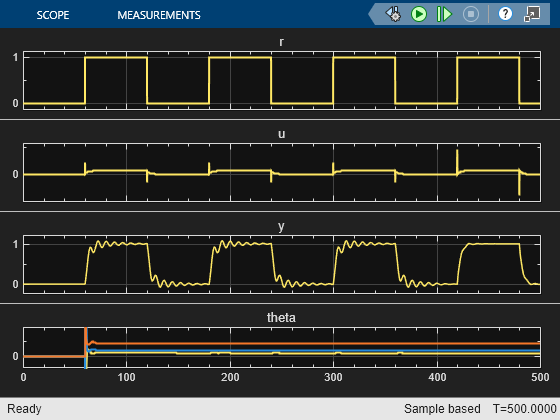
PIDGains = SimOut.logsout{1}.Values.Data(:,:,end);
Kp = PIDGains(1)

Kp = 
0.0623

Ki = PIDGains(2)

Ki = 
0.1119

Kd = PIDGains(3)

Kd = 
0.2253

As demonstrated in the scope, the feedback loop performance improves with the tuned PID controller gains. The scope at the bottom shows the quick convergence of tuned gains during the experiment.

Use Generic Form Linear Controller Option to Tune PID Controller

The VRFT block also supports more general types of linear controllers, making it possible to tune a wider range of linear controllers. For instance, it is straightforward to tune PID controllers in other flavors as long as the the controller can be transformed into the supported format.

mdl2 = "ClosedLoopTuningOfGenericFormControllerUsingVRFT";
open_system(mdl2);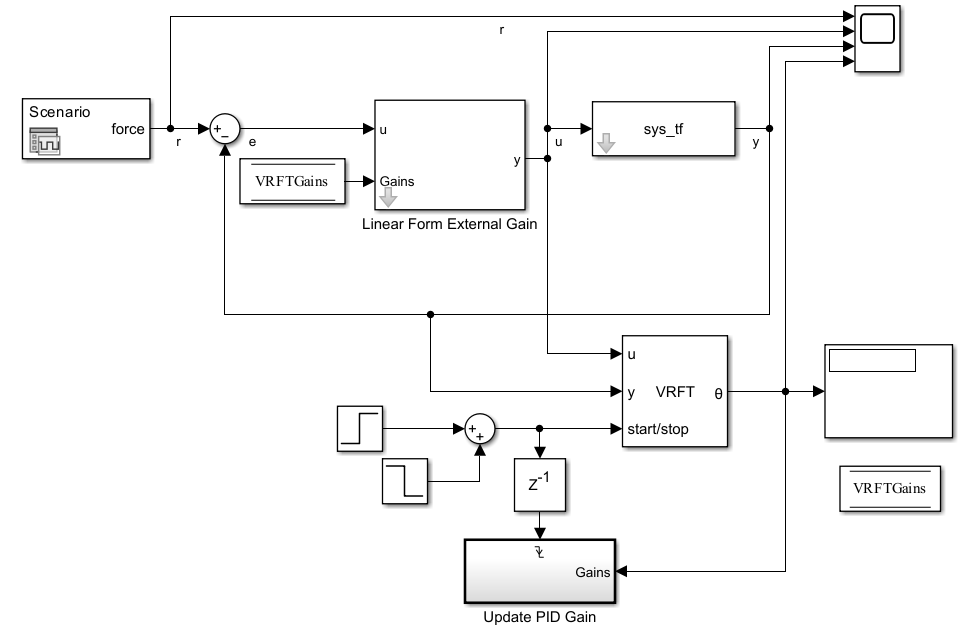

The model contains a subsystem that defines a generic-form linear controller. To tune this controller, you must specify a matching structure in the VRFT block. The generic-form controller in the VRFT block is defined in the form of a cell array of LTI system objects, such as {tf([1],[1],0.1);0.1/2*tf([1 1],[1 -1],0.1);2/0.1*tf([1 -1],[3 -1],0.1)}. This cell array simply represents an identical controller as the PID controller in the previous section, that is, a combination of proportional, integral, and derivative components as the separate entries of the cell array.

Similar to the previous model used for tuning a PID controller, this model also uses a start-stop signal from t = 1 sec to 400 sec. The model updates the tuned controller gains directly at the end of the tuning period. Simulate the model to see the tuned PID controller gains which are directly applied to the generic-form linear controller.

SimOut2 = sim(mdl2);

PIDGains = SimOut2.logsout{1}.Values.Data(:,:,end);
Kp = PIDGains(1)

Kp = 
0.0578

Ki = PIDGains(2)

Ki = 
0.1119

Kd = PIDGains(3)

Kd = 
0.2260

As demonstrated in the scope, the tuning result using the generic-form controller is identical to using the PID controller.

The VRFT block provides an easy approach for tuning parallel-form PID controllers as well as more general type of linear controllers. The generic form option provides enough flexibility to cover a wide range of use cases. Additionally, as shown in this example, when you collect data sequences from the plant model in a closed-loop configuration, you can use VRFT block to improve performance of an existing controller without breaking its feedback loop.