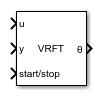
Virtual Reference Feedback Tuning

Automatically tune linearly parameterized controllers based on input-output data

Since R2025a

• 

Libraries:
Simulink Control Design / Autotuning

Description

Virtual reference feedback tuning (VRFT) is a direct data-driven control technique that allows you to tune linearly parameterized controllers based on the plant input and output data. You can use the Virtual Reference Feedback Tuning block to implement VRFT. The major benefits of the Virtual Reference Feedback Tuning block include the ability to perform one-shot tuning, requiring only a single experiment; suitability for tuning linear combinations of linear control laws, including PID and FIR; and support for both online and offline workflows. Using this block, you can tune a controller parameterized in one of the following forms:

• PID Controller — Tune parallel-form PID controllers.

  $$\begin{array}{l}C\left(\theta ,z\right)=P+I\alpha (z)+D\frac{1}{T_s}\frac{z-1}{z}\\ \begin{array}{ccc}{\theta }_1=P& {\theta }_2=I& {\theta }_3=D\end{array}\end{array}$$

  Here, α(z) is the discrete-time integrator formula.

• FIR Filter — Tune FIR Filter.

  $$\begin{array}{l}C(z,b)=b_0+\frac{b_1}{z}+\dots +\frac{b_n}{z^n}\\ \begin{array}{cccc}{\theta }_1=b_0,& {\theta }_2=b_1,& \mathrm{...}& {\theta }_{n+1}=b_n\end{array}\end{array}$$

• Generic Form — Tune a generic-from controller. This can represent a combination of linearly parameterized controllers.

  $$C(z,\theta )={\theta }_1{C}_1(z)+{\theta }_2{C}_2(z)+\dots +{\theta }_n{C}_n(z)$$

For more information about VRFT, see Virtual Reference Feedback Tuning.

Examples

New

Tune PID Controller for Mass-Spring-Damper System Using Virtual Reference Feedback Tuning Block

Tune PID controller for mass-spring-damper using VRFT.

• Since R2025a
• Open Live Script

New

Tune FIR Filter Type Controller for Flexible Transmission System Using Virtual Reference Feedback Tuning Block

Tune FIR filter type controller using VRFT.

• Since R2025a
• Open Live Script

New

Tune PID Controller for Vehicle Lateral Control System Using Virtual Reference Feedback Tuning Block

Use the Virtual Reference Feedback Tuning block to tune PID controller for a vehicle lateral control system.

• Since R2025a
• Open Live Script

Ports

Input

u — Plant input signal

scalar signal

Provide the plant input signal data at this port. For this block, you can provide input-output data either during the simulation (online tuning) or as pre-logged data (offline tuning).

y — Plant output signal

scalar signal

Provide the plant output signal data at this port. For this block, you can provide input-output data either during the simulation (online tuning) or as pre-logged data (offline tuning).

start/stop — Tuning interval signal

scalar signal

To start and stop the tuning process, provide a signal at the start/stop port. When the value of the signal changes from:

• Negative or zero to positive, the tuning starts

• Positive to negative or zero, the signal generation stops

Typically, you can use a signal that changes from 0 to 1 to start the tuning, and from 1 to 0 to stop it. You can also use the Start-Stop Generator block to generate this signal.

Generate a tuning interval signal which is long enough for the algorithm to collect sufficient data such that all θ values converge.

Output

θ — Tuned controller parameters

vector

Tuned controller parameters, returned as an n-by-1 vector signal, where n is the number of controller parameters.

Parameters

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Sample time (Ts) — Sample time

0.1 (default) | positive scalar

Sample time of the block, specified as a positive scalar. The block uses this value to sample the input-output data. This value must match the sample time of the controller you are tuning.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	DiscreteTs
Values:	"0.1" (default) | positive scalar in quotes

Example: set_param(gcb,"DiscreteTs","0.5")

Reference Model — Reference model

tf(1,[3 1]) (default) | tf model object | ss model object | zpk model object

Reference model, specified as a tf, ss, or zpk object. The reference model describes the desired closed loop behavior of the system from reference r(t) to output y(t). For this parameter, you can either provide a continuous-time or discrete-time model as an input. When the input is a continuous-time model, the block discretizes the model using Tustin discretization. When you want to provide a discrete-time model, the sample time must match the Sample Time parameter value.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	MrefS
Values:	"tf(1,[3 1])" (default) | tf, ss, or zpk model object in quotes

Example: set_param(gcb,"MrefS","zpk([],-3,3)")

Weighting Function — Weighting function

1 (default) | tf model object | ss model object | zpk model object

Weighting function, specified as a tf, ss, or zpk object. You can use this parameter to emphasize particular frequencies where matching the r(t)-to-y(t) transfer function with the reference model is most important.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	WeightS
Values:	"1" (default) | tf, ss, or zpk model object in quotes

Example: set_param(gcb,"WeightS","tf([0.1 3],[1 0.03])")

Controller Structure — Controller structure

PID (default) | FIR Filter | Generic Form

Controller structure to tune, specified as one of the following:

• PID Controller — Tune parallel-form PID controllers.

  $$\begin{array}{l}C\left(\theta ,z\right)=P+I\alpha (z)+D\frac{1}{T_s}\frac{z-1}{z}\\ \begin{array}{ccc}{\theta }_1=P& {\theta }_2=I& {\theta }_3=D\end{array}\end{array}$$

  Here, α(z) is the discrete-time integrator formula.

• FIR Filter — Tune FIR Filter.

  $$\begin{array}{l}C(z,b)=b_0+\frac{b_1}{z}+\dots +\frac{b_n}{z^n}\\ \begin{array}{cccc}{\theta }_1=b_0,& {\theta }_2=b_1,& \mathrm{...}& {\theta }_{n+1}=b_n\end{array}\end{array}$$

• Generic Form — Tune a generic-from controller. This can represent a combination of linearly parameterized controllers.

  $$C(z,\theta )={\theta }_1{C}_1(z)+{\theta }_2{C}_2(z)+\dots +{\theta }_n{C}_n(z)$$

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	ControlType
Values:	"PID" (default) | "FIR Filter" | "Generic Form"

Example: set_param(gcb,"ControlType","Generic Form")

Type — PID controller type

PI (default) | P | I | PD | PID

Specify which of the proportional, integral, and derivative terms are in the controller.

• P — Proportional action only.

• I — Integral action only.

• PI — Proportional and integral action only.

• PD — Proportional and derivative action only.

• PID — Proportional, integral, and derivative action.

Dependencies

To enable this parameter, set Controller Structure to PID.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	PIDControlType
Values:	"PI" (default) | "P" | "I" | "PD" | "PID"

Example: set_param(gcb,"PIDControlType","PID")

Integrator Method — Discrete integration method

Forward Euler (default) | Backward Euler | Trapezoidal

Discrete integrator formula α(z) for integration in discrete-time PID controller:

$$C(z)=P+I\alpha (z)+D\frac{1}{T_s}\frac{z-1}{z}$$

Specify Integrator Method as one of the following:

• Forward Euler — $$\alpha (z)=\frac{T_s}{z-1}$$.

• Backward Euler — $$\alpha (z)=\frac{T_{s}z}{z-1}$$.

• Trapezoidal — $$\alpha (z)=\frac{T_s}{2}\frac{z+1}{z-1}$$.

For more information about discrete-time integration, see the Discrete-Time Integrator block reference page.

Dependencies

To enable this parameter, set Controller Structure to PID and set Type to a controller type with integral action.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	PIDIntegratorMethod
Values:	"Forward Euler" (default) | "Backward Euler" | "Trapezoidal"

Example: set_param(gcb,"PIDIntegratorMethod","Trapezoidal")

FIR Filter Order — FIR filter order

2 (default) | positive integer between 2 and 10

Order of the FIR filter to tune, specified as a positive integer between 2 and 10.

Dependencies

To enable this parameter, set Controller Structure to FIR Filter.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	FIRFilterOrder
Values:	"2" (default) | positive integer between 2 and 10 in quotes

Example: set_param(gcb,"FIRFilterOrder","5")

SISO Linear Systems Ci(z) — Array of SISO linear systems

{tf([1],[1],0.1);0.1*tf([1],[1 -1],0.1)} (default) | cell array | LTI model array

Linear systems C_i(z) in the generic-form control structure, specified as a cell array of LTI objects (ss, tf, zpk) or an LTI model array.

$$C(z,\theta )={\theta }_1{C}_1(z)+{\theta }_2{C}_2(z)+\dots +{\theta }_n{C}_n(z)$$

Specify this parameter such that the value matches the form of the controller to tune. This can also represent a combination of linearly parameterized controllers. Here, the controller parameters θ_i are ordered corresponding to the index of LTI objects provided in the array. For example, the default value of this parameter represents a discrete-time parallel-form PID controller, with θ₁ as the proportional gain and θ₂ as the integral gain.

Dependencies

To enable this parameter, set Controller Structure to Generic Form.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	LTIInputObj
Values:	"{tf([1],[1],0.1);0.1*tf([1],[1 -1],0.1)}" (default) | cell array in quotes | LTI model array in quotes

Example: set_param(gcb,"LTIInputObj","{tf([1],[1],0.1);(1/0.1)*tf([1 -1],[1 0],0.1)}")

Show θ values while tuning — Output tuned parameter values

on (default) | off

Enable this option to output the transient values of θ at the block output port θ when tuning.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	ShowThetaWhileTuning
Values:	"on" (default) | "off"

Example: set_param(gcb,"ShowThetaWhileTuning","off")

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2025a