cvshrink

Cross-validate regularization of linear discriminant

Syntax

err = cvshrink(mdl)

[err,gamma] = cvshrink(mdl)

[err,gamma,delta] = cvshrink(mdl)

[err,gamma,delta,numpred] = cvshrink(mdl)

[___] = cvshrink(mdl,Name=Value)

Description

err = cvshrink(mdl) returns a vector of cross-validated classification error values for differing values of the regularization parameter gamma.

[err,gamma] = cvshrink(mdl) also returns the vector of gamma values.

[err,gamma,delta] = cvshrink(mdl) also returns the vector of delta values.

[err,gamma,delta,numpred] = cvshrink(mdl) returns the vector of number of nonzero predictors for each setting of the parameters gamma and delta.

[___] = cvshrink(mdl,Name=Value) specifies additional options using one or more name-value arguments. For example, you can specify the number of delta and gamma intervals for cross-validation, and the verbosity level of progress messages.

Examples

Regularize Data with Many Predictors

Regularize a discriminant analysis classifier, and view the tradeoff between the number of predictors in the model and the classification accuracy.

Create a linear discriminant analysis classifier for the ovariancancer data. Set the SaveMemory and FillCoeffs options to keep the resulting model reasonably small.

load ovariancancer
obj = fitcdiscr(obs,grp,...
    'SaveMemory','on','FillCoeffs','off');

Use 10 levels of Gamma and 10 levels of Delta to search for good parameters. This search is time-consuming. Set Verbose to 1 to view the progress.

rng('default') % for reproducibility
[err,gamma,delta,numpred] = cvshrink(obj,...
    'NumGamma',9,'NumDelta',9,'Verbose',1);

Done building cross-validated model.
Processing Gamma step 1 out of 10.
Processing Gamma step 2 out of 10.
Processing Gamma step 3 out of 10.
Processing Gamma step 4 out of 10.
Processing Gamma step 5 out of 10.
Processing Gamma step 6 out of 10.
Processing Gamma step 7 out of 10.
Processing Gamma step 8 out of 10.
Processing Gamma step 9 out of 10.
Processing Gamma step 10 out of 10.

Plot the classification error rate against the number of predictors.

plot(err,numpred,'k.')
xlabel('Error rate');
ylabel('Number of predictors');

Input Arguments

mdl — Trained discriminant analysis classifier

ClassificationDiscriminant model object

Trained discriminant analysis classifier, specified as a ClassificationDiscriminant model object, trained with fitcdiscr.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: [err,gamma,delta,numpred] = cvshrink(mdl,NumGamma=9,NumDelta=9,Verbose=1);

delta — Delta values for cross-validation

0 (default) | numeric row vector | numeric matrix

Delta values for cross-validation, specified as a numeric scalar, row vector, or matrix.

• Scalar delta — cvshrink uses this value of delta with every value of gamma for regularization.

• Row vector delta — For each i and j, cvshrink uses delta(j) with gamma(i) for regularization.

• Matrix delta — The number of rows of delta must equal the number of elements in gamma. For each i and j, cvshrink uses delta(i,j) with gamma(i) for regularization.

Example: delta=[0 .01 .1]

Data Types: double

gamma — Gamma values for cross-validation

0:0.1:1 (default) | numeric vector

Gamma values for cross-validation, specified as a numeric vector.

Example: gamma=[0 .01 .1]

Data Types: double

NumDelta — Number of delta intervals for cross-validation

0 (default) | nonnegative integer

Number of delta intervals for cross-validation, specified as a nonnegative integer. For every value of gamma, cvshrink cross-validates the discriminant using NumDelta + 1 values of delta, uniformly spaced from zero to the maximal delta at which all predictors are eliminated for this value of gamma. If you set delta, cvshrink ignores NumDelta.

Example: NumDelta=3

Data Types: double

NumGamma — Number of gamma intervals for cross-validation

10 (default) | nonnegative integer

Number of gamma intervals for cross-validation, specified as a nonnegative integer. cvshrink cross-validates the discriminant using NumGamma + 1 values of gamma, uniformly spaced from MinGamma to 1. If you set gamma, cvshrink ignores NumGamma.

Example: NumGamma=3

Data Types: double

Verbose — Verbosity level

0 (default) | 1 | 2

Verbosity level, specified as 0, 1, or 2. Higher values give more progress messages.

Example: Verbose=2

Data Types: double

Output Arguments

err — Misclassification error rate

numeric vector | numeric matrix

Misclassification error rate, returned as a numeric vector or matrix of errors. The misclassification error rate is the average fraction of misclassified data over all folds.

• If delta is a scalar (default), err(i) is the misclassification error rate for mdl regularized with gamma(i).

• If delta is a vector, err(i,j) is the misclassification error rate for mdl regularized with gamma(i) and delta(j).

• If delta is a matrix, err(i,j) is the misclassification error rate for mdl regularized with gamma(i) and delta(i,j).

gamma — Gamma values used for regularization

numeric vector

Gamma values used for regularization, returned as a numeric vector. See Gamma and Delta.

delta — Delta values used for regularization

numeric vector | numeric matrix

Delta values used for regularization, returned as a numeric vector or matrix. See Gamma and Delta.

• If you specify a scalar for the delta name-value argument, the output delta is a row vector the same size as gamma, with entries equal to the input scalar.

• If you specify a row vector for the delta name-value argument, the output delta is a matrix with the same number of columns as the row vector, and with the number of rows equal to the number of elements of gamma. The output delta(i,j) is equal to the input delta(j).

• If you specify a matrix for the delta name-value argument, the output delta is the same as the input matrix. The number of rows of delta must equal the number of elements in gamma.

numpred — Number of predictors in model at various regularizations

numeric vector | numeric matrix

Number of predictors in the model at various regularizations, returned as a numeric vector or matrix. numpred has the same size as err.

• If delta is a scalar (default), numpred(i) is the number of predictors for mdl regularized with gamma(i) and delta.

• If delta is a vector, numpred(i,j) is the number of predictors for mdl regularized with gamma(i) and delta(j).

• If delta is a matrix, numpred(i,j) is the number of predictors for mdl regularized with gamma(i) and delta(i,j).

More About

Gamma and Delta

Regularization is the process of finding a small set of predictors that yield an effective predictive model. For linear discriminant analysis, there are two parameters, γ and δ, that control regularization as follows. cvshrink helps you select appropriate values of the parameters.

Let Σ represent the covariance matrix of the data X, and let $$\widehat{X}$$ be the centered data (the data X minus the mean by class). Define

$$D=\text{diag}\left({\widehat{X}}^T*\widehat{X}\right).$$

The regularized covariance matrix $$\tilde{\Sigma }$$ is

$$\tilde{\Sigma }=\left(1-\gamma \right)\Sigma +\gamma D.$$

Whenever γ ≥ MinGamma, $$\tilde{\Sigma }$$ is nonsingular.

Let μ_k be the mean vector for those elements of X in class k, and let μ₀ be the global mean vector (the mean of the rows of X). Let C be the correlation matrix of the data X, and let $$\tilde{C}$$ be the regularized correlation matrix:

$$\tilde{C}=\left(1-\gamma \right)C+\gamma I,$$

where I is the identity matrix.

The linear term in the regularized discriminant analysis classifier for a data point x is

$${\left(x-{\mu }_0\right)}^T{\tilde{\Sigma }}^{-1}\left({\mu }_k-{\mu }_0\right)=\left[{\left(x-{\mu }_0\right)}^T{D}^{-1/2}\right]\left[{\tilde{C}}^{-1}{D}^{-1/2}\left({\mu }_k-{\mu }_0\right)\right].$$

The parameter δ enters into this equation as a threshold on the final term in square brackets. Each component of the vector $$\left[{\tilde{C}}^{-1}{D}^{-1/2}\left({\mu }_k-{\mu }_0\right)\right]$$ is set to zero if it is smaller in magnitude than the threshold δ. Therefore, for class k, if component j is thresholded to zero, component j of x does not enter into the evaluation of the posterior probability.

The DeltaPredictor property is a vector related to this threshold. When δ ≥ DeltaPredictor(i), all classes k have

$$\left|{\tilde{C}}^{-1}{D}^{-1/2}\left({\mu }_k-{\mu }_0\right)\right|\le \delta .$$

Therefore, when δ ≥ DeltaPredictor(i), the regularized classifier does not use predictor i.

Tips

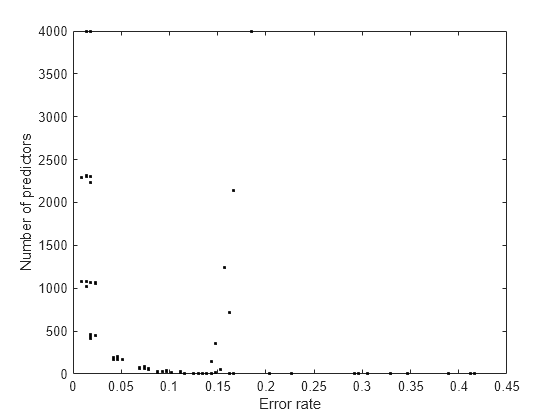
• Examine the err and numpred outputs to see the tradeoff between the cross-validated error and the number of predictors. When you find a satisfactory point, set the corresponding gamma and delta properties in the model using dot notation. For example, if (i,j) is the location of the satisfactory point, set:

  mdl.Gamma = gamma(i);
  mdl.Delta = delta(i,j);

Version History

Introduced in R2012b