predict
Predict responses for new observations from naive Bayes incremental learning classification model
Since R2021a
Description
label = predict(Mdl,X,Name,Value)Mdl.Cost) for computing predictions by specifying the
Cost argument.
[
also returns the posterior probabilities
(label,Posterior,Cost] = predict(___)Posterior) and predicted (expected) misclassification costs
(Cost) corresponding to the observations (rows) in
X using any of the input argument combinations in the previous
syntaxes. For each observation in X, the predicted class label
corresponds to the minimum expected classification cost among all classes.
Examples
Load the human activity data set.
load humanactivityFor details on the data set, enter Description at the command line.
Fit a naive Bayes classification model to the entire data set.
TTMdl = fitcnb(feat,actid)
TTMdl =
ClassificationNaiveBayes
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
NumObservations: 24075
DistributionNames: {1×60 cell}
DistributionParameters: {5×60 cell}
Properties, Methods
TTMdl is a ClassificationNaiveBayes model object representing a traditionally trained model.
Convert the traditionally trained model to a naive Bayes classification model for incremental learning.
IncrementalMdl = incrementalLearner(TTMdl)
IncrementalMdl =
incrementalClassificationNaiveBayes
IsWarm: 1
Metrics: [1×2 table]
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
DistributionNames: {1×60 cell}
DistributionParameters: {5×60 cell}
Properties, Methods
IncrementalMdl is an incrementalClassificationNaiveBayes model object prepared for incremental learning.
The incrementalLearner function initializes the incremental learner by passing learned conditional predictor distribution parameters to it, along with other information TTMdl learned from the training data. IncrementalMdl is warm (IsWarm is 1), which means that incremental learning functions can start tracking performance metrics.
An incremental learner created from converting a traditionally trained model can generate predictions without further processing.
Predict class labels for all observations using both models.
ttlabels = predict(TTMdl,feat); illables = predict(IncrementalMdl,feat); sameLabels = sum(ttlabels ~= illables) == 0
sameLabels = logical
1
Both models predict the same labels for each observation.
This example shows how to apply misclassification costs for label prediction on incoming chunks of data, while maintaining a balanced misclassification cost for training.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(10); % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
Create a naive Bayes classification model for incremental learning. Specify the class names. Prepare the model for predict by fitting the model to the first 10 observations.
Mdl = incrementalClassificationNaiveBayes(ClassNames=unique(Y)); initobs = 10; Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs)); canPredict = size(Mdl.DistributionParameters,1) == numel(Mdl.ClassNames)
canPredict = logical
1
Consider severely penalizing the model for misclassifying "running" (class 4). Create a cost matrix that applies 100 times the penalty for misclassifying running as compared to misclassifying any other class. Rows correspond to the true class, and columns correspond to the predicted class.
k = numel(Mdl.ClassNames);
Cost = ones(k) - eye(k);
Cost(4,:) = Cost(4,:)*100; % Penalty for misclassifying "running"
CostCost = 5×5
0 1 1 1 1
1 0 1 1 1
1 1 0 1 1
100 100 100 0 100
1 1 1 1 0
Simulate a data stream, and perform the following actions on each incoming chunk of 100 observations.
Call
predictto predict labels for each observation in the incoming chunk of data.Call
predictagain, but specify the misclassification costs by using theCostargument.Call
fitto fit the model to the incoming chunk. Overwrite the previous incremental model with a new one fitted to the incoming observations.
numObsPerChunk = 100; nchunk = ceil((n - initobs)/numObsPerChunk); labels = zeros(n,1); cslabels = zeros(n,1); cst = zeros(n,5); cscst = zeros(n,5); % Incremental learning for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; [labels(idx),~,cst(idx,:)] = predict(Mdl,X(idx,:)); [cslabels(idx),~,cscst(idx,:)] = predict(Mdl,X(idx,:),Cost=Cost); Mdl = fit(Mdl,X(idx,:),Y(idx)); end labels = labels((initobs + 1):end); cslabels = cslabels((initobs + 1):end);
Compare the predicted class distributions between the prediction methods by plotting histograms.
figure; histogram(labels); hold on histogram(cslabels); legend(["Default-cost prediction" "Cost-sensitive prediction"])

Because the cost-sensitive prediction method penalizes misclassifying class 4 so severely, more predictions into class 4 result as compared to the prediction method that uses the default, balanced cost.
Load the human activity data set. Randomly shuffle the data.
load humanactivity n = numel(actid); rng(10) % For reproducibility idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Create a naive Bayes classification model for incremental learning. Specify the class names. Prepare the model for predict by fitting the model to the first 10 observations.
Mdl = incrementalClassificationNaiveBayes('ClassNames',unique(Y));
initobs = 10;
Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));
canPredict = size(Mdl.DistributionParameters,1) == numel(Mdl.ClassNames)canPredict = logical
1
Mdl is an incrementalClassificationNaiveBayes model. All its properties are read-only. The model is configured to generate predictions.
Simulate a data stream, and perform the following actions on each incoming chunk of 100 observations.
Call
predictto compute class posterior probabilities for each observation in the incoming chunk of data.Call
rocmetricsto compute the area under the ROC curve (AUC) using the class posterior probabilities, and store the AUC value, averaged over all classes. This AUC is an incremental measure of how well the model predicts the activities on average.Call
fitto fit the model to the incoming chunk. Overwrite the previous incremental model with a new one fitted to the incoming observations.
numObsPerChunk = 100; nchunk = floor((n - initobs)/numObsPerChunk); auc = zeros(nchunk,1); classauc = 5; % Incremental learning for j = 1:nchunk ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs); iend = min(n,numObsPerChunk*j + initobs); idx = ibegin:iend; [~,posterior] = predict(Mdl,X(idx,:)); mdlROC = rocmetrics(Y(idx),posterior,Mdl.ClassNames); [~,~,~,auc(j)] = average(mdlROC,'micro'); Mdl = fit(Mdl,X(idx,:),Y(idx)); end
Now, Mdl is an incrementalClassificationNaiveBayes model object trained on all the data in the stream.
Plot the AUC values for each incoming chunk of data.
plot(auc) xlim([0 nchunk]) ylabel('AUC') xlabel('Iteration')
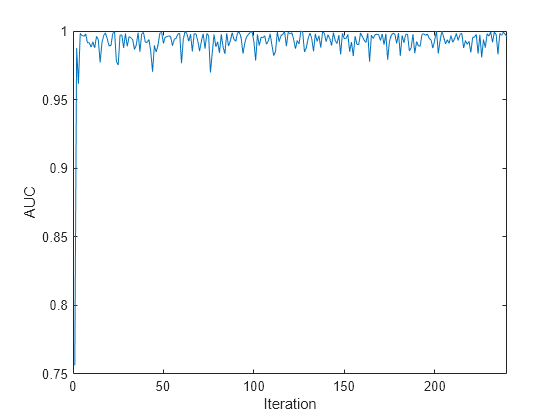
The plot suggests that the classifier predicts the activities well during incremental learning.
Input Arguments
Naive Bayes classification model for incremental learning, specified as an incrementalClassificationNaiveBayes model object. You can create Mdl directly or by converting a supported, traditionally trained machine learning model using the incrementalLearner function. For more details, see the corresponding reference page.
You must configure Mdl to predict labels for a batch of observations.
If
Mdlis a converted, traditionally trained model, you can predict labels without any modifications.Otherwise,
Mdl.DistributionParametersmust be a cell matrix withMdl.NumPredictors> 0 columns and at least one row, where each row corresponds to each class name inMdl.ClassNames.
Batch of predictor data for which to predict labels, specified as an n-by-Mdl.NumPredictors floating-point matrix.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Cost=[0 2;1 0] attributes double the penalty for
misclassifying observations with true class Mdl.ClassNames(1), than for
misclassifying observations with true class
Mdl.ClassNames(2).
Cost of misclassifying an observation, specified as a value in the table, where
c is the number of classes in Mdl.ClassNames.
The specified value overrides the value of Mdl.Cost.
| Value | Description |
|---|---|
| c-by-c numeric matrix |
|
| Structure array | A structure array having two fields:
|
Example: Cost=struct('ClassNames',Mdl.ClassNames,'ClassificationCosts',[0 2; 1 0])
Data Types: single | double | struct
Prior class probabilities, specified as a value in this numeric vector. Prior has the same length as the number of classes in Mdl.ClassNames, and the order of the elements corresponds to the class order in Mdl.ClassNames. predict normalizes the vector so that the sum of the result is 1.
The specified value overrides the value of Mdl.Prior.
Data Types: single | double
Score transformation function describing how incremental learning functions transform raw response values, specified as a character vector, string scalar, or function handle. The specified value overrides the value of Mdl.ScoreTransform.
This table describes the available built-in functions for score transformation.
| Value | Description |
|---|---|
"doublelogit" | 1/(1 + e–2x) |
"invlogit" | log(x / (1 – x)) |
"ismax" | Sets the score for the class with the largest score to 1, and sets the scores for all other classes to 0 |
"logit" | 1/(1 + e–x) |
"none" or "identity" | x (no transformation) |
"sign" | –1 for x < 0 0 for x = 0 1 for x > 0 |
"symmetric" | 2x – 1 |
"symmetricismax" | Sets the score for the class with the largest score to 1, and sets the scores for all other classes to –1 |
"symmetriclogit" | 2/(1 + e–x) – 1 |
Data Types: char | string
Output Arguments
Predicted responses (labels), returned as a categorical or character array;
floating-point, logical, or string vector; or cell array of character vectors with
n rows. n is the number of observations in
X, and label( is
the predicted response for observation j)j
label has the same data type as the class names stored in
Mdl.ClassNames. (The software treats string arrays as cell arrays of character
vectors.)
Class posterior probabilities,
returned as an n-by-numel(Mdl.ClassNames)
floating-point matrix.
Posterior(
is the posterior probability that observation
j,k)jkMdl.ClassNames
specifies the order of the classes.
Expected misclassification costs, returned as an n-by-numel(Mdl.ClassNames) floating-point matrix.
Cost(
is the expected cost of the observation in row
j,k)jX being
classified into class kMdl.ClassNames().k)
More About
A misclassification cost is the relative severity of a classifier labeling an observation into the wrong class.
Two types of misclassification cost exist: true and expected. Let K be the number of classes.
True misclassification cost — A K-by-K matrix, where element (i,j) indicates the cost of classifying an observation into class j if its true class is i. The software stores the misclassification cost in the property
Mdl.Cost, and uses it in computations. By default,Mdl.Cost(i,j)= 1 ifi≠j, andMdl.Cost(i,j)= 0 ifi=j. In other words, the cost is0for correct classification and1for any incorrect classification.Expected misclassification cost — A K-dimensional vector, where element k is the weighted average cost of classifying an observation into class k, weighted by the class posterior probabilities.
In other words, the software classifies observations into the class with the lowest expected misclassification cost.
The posterior probability is the probability that an observation belongs in a particular class, given the data.
For naive Bayes, the posterior probability that a classification is k for a given observation (x1,...,xP) is
where:
is the conditional joint density of the predictors given they are in class k.
Mdl.DistributionNamesstores the distribution names of the predictors.π(Y = k) is the class prior probability distribution.
Mdl.Priorstores the prior distribution.is the joint density of the predictors. The classes are discrete, so
Version History
Introduced in R2021a
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)