Markov Chains
Markov processes are examples of stochastic processes—processes that generate random sequences of outcomes or states according to certain probabilities. Markov processes are distinguished by being memoryless—their next state depends only on their current state, not on the history that led them there. Models of Markov processes are used in a wide variety of applications, from daily stock prices to the positions of genes in a chromosome.
A Markov model is given visual representation with a state diagram, such as the one below.
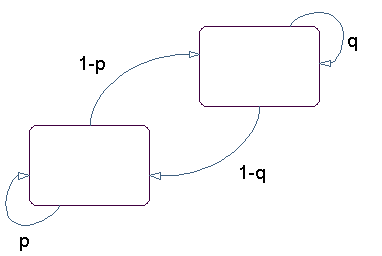
The rectangles in the diagram represent the possible states of the process you are trying to model, and the arrows represent transitions between states. The label on each arrow represents the probability of that transition. At each step of the process, the model may generate an output, or emission, depending on which state it is in, and then make a transition to another state. An important characteristic of Markov models is that the next state depends only on the current state, and not on the history of transitions that lead to the current state.
For example, for a sequence of coin tosses the two states are heads and tails. The most recent coin toss determines the current state of the model and each subsequent toss determines the transition to the next state. If the coin is fair, the transition probabilities are all 1/2. The emission might simply be the current state. In more complicated models, random processes at each state will generate emissions. You could, for example, roll a die to determine the emission at any step.
Markov chains are mathematical descriptions of Markov models with a discrete set of states. Markov chains are characterized by:
A set of states {1, 2, ..., M}
An M-by-M transition matrix T whose i,j entry is the probability of a transition from state i to state j. The sum of the entries in each row of T must be 1, because this is the sum of the probabilities of making a transition from a given state to each of the other states.
A set of possible outputs, or emissions, {s1, s2, ... , sN}. By default, the set of emissions is {1, 2, ... , N}, where N is the number of possible emissions, but you can choose a different set of numbers or symbols.
An M-by-N emission matrix E whose i,k entry gives the probability of emitting symbol sk given that the model is in state i.
Markov chains begin in an initial state i0 at step 0. The chain then transitions to state i1 with probability , and emits an output with probability . Consequently, the probability of observing the sequence of states and the sequence of emissions in the first r steps, is