slicesample
Slice sampler
Syntax
Description
rnd = slicesample(initial,nsamples,"pdf",pdf)nsamples random samples from the
density function pdf using the slice sampling method (see Algorithms).
initial is a scalar or vector specifying the initial point
from which the function starts sampling.
rnd = slicesample(initial,nsamples,"logpdf",logpdf)nsamples random samples from the log density function
logpdf. During sampling, slicesample
uses logpdf to evaluate the logarithm of the density function
directly, instead of first evaluating the density function and then taking the log.
You can use this syntax if the density function is already in logarithmic form (see
Tips).
rnd = slicesample(___,Name,Value)
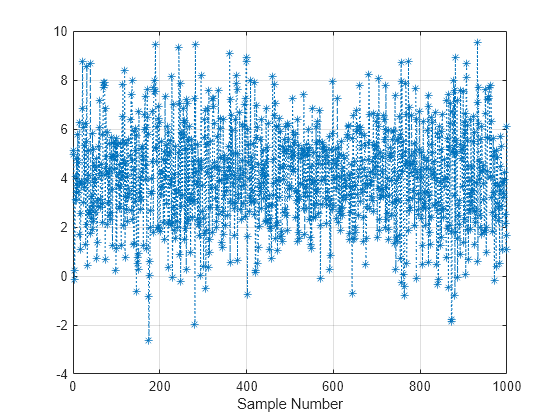
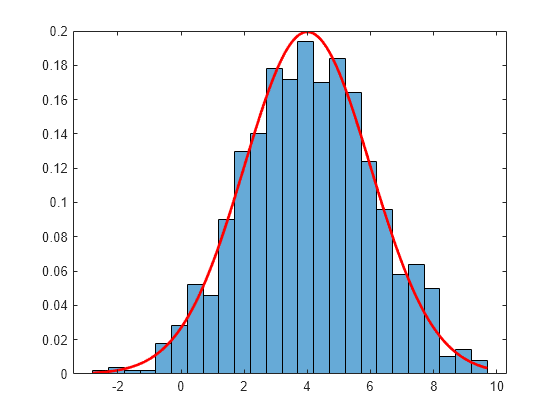
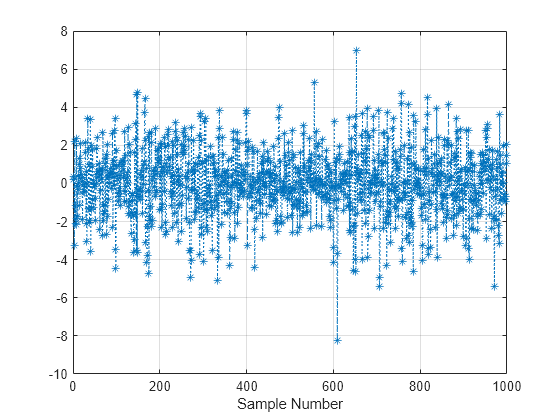
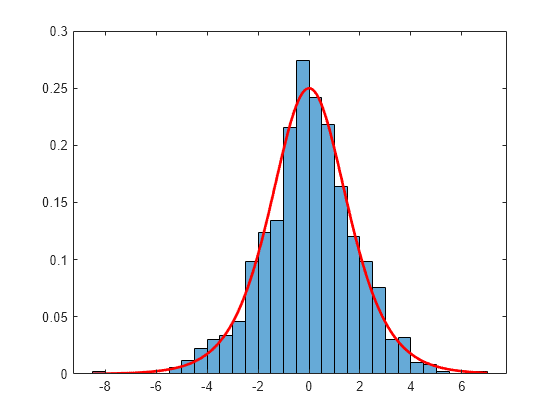
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Tips
Use
logpdfinstead ofpdffor density functions where numerical overflow or underflow errors might occur.There are no definitive guidelines for determining appropriate values for
thinandburnin. Specify starting values forthinandburninand then increase them, if necessary, to achieve the requisite sample independence and similarity to the target density function.If the step-out procedure (see Algorithms) fails, by exceeding the maximum number of 200 function evaluations while generating a sample, you might have to experiment with different values of
width. Ifwidthis too small, the algorithm might implement an excessive number of function evaluations to determine the extent of the slice. Ifwidthis too large, the algorithm tries to decrease the width to an appropriate size, which might also result in a large number of function evaluations. Thenevaloutput argument returns the average number of function evaluations per sample.
Algorithms
Slice sampling is a Markov Chain Monte Carlo (MCMC) algorithm that samples from a distribution with an arbitrary density function, known only up to a constant of proportionality. This situation can arise when sampling is needed from a complicated Bayesian posterior distribution whose normalization constant is unknown. The algorithm does not generate independent samples, but rather a Markov chain whose stationary distribution is the target distribution.
The slicesample function draws samples from the region under the
density function using a sequence of vertical and horizontal steps. First, the algorithm
selects a height at random between 0 and the value of the density function
f(x) at a specified initial value of
x. Then, the algorithm selects a new x value
at random by sampling from the horizontal “slice” that contains all
x values where the density function is greater than the selected
height. The slicesample function uses a similar slice sampling
algorithm in the case of a multivariate distribution.
Choose a density function f(x) that is proportional to the target density function, and do the following to generate a Markov chain of random numbers:
Select an initial value x(t) that lies within the domain of f(x).
Draw a real value y uniformly from (0, f(x(t))), thereby defining a horizontal “slice” as S = {x: y < f(x)}.
Find an interval I = (L, R) around x(t) that contains all or much of the “slice” S.
Draw a new point x(t + 1) from within this interval.
Increment t by 1, and repeat steps 2 through 4 until you get the number of samples you want.
slicesample uses the slice sampling algorithm of Neal [1]. For numerical
stability, slicesample operates on the logarithm of the
pdf function (unless the logpdf argument
is specified). slicesample uses Neal's “stepping-out”
and “stepping-in” method to find the interval I
containing the slice S. The algorithm tries a maximum of 200 step-out
and 200 step-in iterations when generating each sample.
Nearby points in the chain tend to have values that are closer together than they
would be from a sample of independent values. For many purposes, the entire set of
points can be used as a sample from the target distribution. However, when this type of
serial correlation is a problem, the burnin and
thin name-value arguments can help reduce the correlation.
Alternative Functionality
slicesamplecan produce Markov chains that mix slowly and take a long time to converge to a stationary distribution, especially for medium-dimensional and high-dimensional density functions. Use the gradient-based Hamiltonian Monte Carlo (HMC) samplerhmcSamplerto speed up sampling in these cases. See Representing Sampling Distributions Using Markov Chain Samplers.
References
[1] Neal, Radford M. "Slice Sampling." The Annals of Statistics Vol. 31, No. 3, pp. 705–767, 2003. Available at https://doi.org/10.1214/aos/1056562461.
Version History
Introduced in R2006a