PartitionedDirectForecaster

Cross-validated direct forecasting model

Since R2023b

Description

PartitionedDirectForecaster is a set of direct forecasting models trained on partitioned, regularly sampled time series data. You can evaluate the quality of the cross-validated direct forecasting model by using the cvloss and cvpredict object functions.

The cvloss and cvpredict object functions use models trained on training observations to predict the response for test observations. For example, suppose you cross-validate a direct forecasting model that predicts one step ahead by using five sliding windows. In this case, the software splits the data set into five windows with fixed-size training and test sets. Cross-validation proceeds as follows:

1. The software trains the first model (stored in CVMdl.Learners{1}) by using the observations in the first training set, and uses the observations in the first test set for validation.

2. The software trains the second model (stored in CVMdl.Learners{2}) by using the observations in the second training set, and uses the observations in the second test set for validation.

3. The software proceeds in a similar way for the third, fourth, and fifth models.

If you validate by using cvpredict, the software computes predictions for the observations in test set i by using model i. If an observation is in more than one test set, then the function returns the prediction for that observation, averaged over all test sets, by default.

Creation

You can create a PartitionedDirectForecaster model in two ways:

• Create a cross-validated model from a direct forecasting object DirectForecaster by using the crossval object function.

• Create a cross-validated model by using the directforecaster function and specifying the Partition name-value argument.

Properties

Partition and Learner Properties

Learners — Compact direct forecasting models used for cross-validation

cell array of CompactDirectForecaster model objects

This property is read-only.

Compact direct forecasting models used for cross-validation, specified as a cell array of CompactDirectForecaster model objects. The number of models in Learners matches the number of test sets in the data partition Partition.

Data Types: cell

LearnerTemplate — Template for regression models

output of template function

This property is read-only.

Template for the regression models in each Learners model, specified as the output of one of these template functions.

Template Function	Description
templateEnsemble	Ensemble learning template, with the ensemble aggregation method specified as "Bag" or "LSBoost"
templateGAM	General additive model template
templateGP	Gaussian process regression model template
templateKernel	Kernel model template
templateLinear	Linear learner template
templateSVM	Support vector machine template
templateTree	Decision tree template

Partition — Data partition

tspartition object

This property is read-only.

Data partition indicating how the software splits the data for cross-validation, specified as a tspartition object. The model uses expanding window cross-validation, sliding window cross-validation, or holdout validation.

Data Properties

CategoricalPredictors — Indices of categorical exogenous predictors

positive integer vector | []

This property is read-only.

Indices of categorical exogenous predictors, specified as a positive integer vector. Each index value in CategoricalPredictors indicates that the corresponding exogenous predictor in X is categorical. (See PredictorNames for the list of exogenous predictors.) If none of the exogenous predictors are categorical, then this property is empty ([]).

Data Types: double

NumObservations — Number of observations

positive integer scalar

This property is read-only.

Number of observations in the data stored in X and Y, specified as a positive integer scalar.

Data Types: double

PredictorNames — Names of exogenous predictors

cell array of character vectors

This property is read-only.

Names of the exogenous predictors, specified as a cell array of character vectors. The order of the elements in PredictorNames corresponds to the order of the exogenous predictors in X.

Data Types: cell

ResponseName — Name of response variable

character vector

This property is read-only.

Name of the response variable, specified as a character vector.

Data Types: char

X — Exogenous predictor data

numeric matrix | table | timetable

This property is read-only.

Exogenous predictor data used to cross-validate the model, specified as a numeric matrix, table, or timetable. Each row of X corresponds to one observation, and each column corresponds to one variable.

Y — Response data

numeric vector | one-column table | one-column timetable

This property is read-only.

Response data used to cross-validate the model, specified as a numeric vector, one-column table, or one-column timetable. Each row of Y corresponds to one observation.

Forecasting and Prepared Data Properties

Horizon — Future time steps at which to forecast

positive integer vector

This property is read-only.

Future time steps at which to forecast, specified as a positive integer vector. Each of the compact direct forecasting models in Learners contains a regression model for each horizon step.

For example, if the Horizon value of a cross-validated direct forecasting model CVMdl is [1 3], then CVMdl.Learners{1}.Learners contains two regression models: one that forecasts at horizon step 1 and one that forecasts at horizon step 3.

Data Types: double

LeadingPredictorLags — Predictor lags used for preparing leading exogenous predictors

nonnegative integer vector | cell array of nonnegative integer vectors | []

This property is read-only.

Leading predictor lags used for preparing leading exogenous predictors, specified as a nonnegative integer vector or cell array of nonnegative integer vectors.

• If LeadingPredictorLags is a vector, then for each element i in the vector, the software shifts the leading exogenous predictors backward in time by i steps, relative to the horizon time step. The software uses the resulting features as predictors. When the LeadingPredictorLags value is 0, the software uses the unshifted leading predictors.

  For example, if the Horizon value of a cross-validated direct forecasting model CVMdl is 3 and the LeadingPredictorLags value is 0, then the software uses the unshifted leading predictor values at horizon step 3 as predictor values.

• If LeadingPredictorLags is a cell array, then the numeric values in element i of the cell array indicate the lags for leading exogenous predictor i.

If no leading predictor lags are used, then this property is empty ([]).

Data Types: double | cell

LeadingPredictors — Indices of leading exogenous predictors

positive integer vector | []

This property is read-only.

Indices of the leading exogenous predictors, specified as a positive integer vector. Leading predictors are predictors for which future values are known. Each index value in LeadingPredictors indicates that the corresponding exogenous predictor in X is leading. (See PredictorNames for the list of exogenous predictors.) If no exogenous predictors are leading predictors, then this property is empty ([]).

Data Types: double

MaxLag — Maximum lag value

nonnegative integer scalar

This property is read-only.

Maximum lag value, specified as a nonnegative integer scalar. The MaxLag value depends on the values in ResponseLags, PredictorLags, and LeadingPredictorLags. Specifically, the software computes the maximum lag as follows:

MaxLag = max([0,ResponseLags,PredictorLags, ...
    LeadingPredictorLags - min(Horizon) + 1])

Unlike response lags and nonleading predictor lags, leading predictor lags are relative to horizon time steps instead of the current time step.

Data Types: double

PredictorLags — Predictor lags used for preparing nonleading exogenous predictors

positive integer vector | cell array of positive integer vectors | []

This property is read-only.

Predictor lags used for preparing nonleading exogenous predictors, specified as a positive integer vector or cell array of positive integer vectors.

• If PredictorLags is a vector, then for each element i in the vector, the software shifts the nonleading exogenous predictors backward in time by i steps and uses the resulting features as predictors.

• If PredictorLags is a cell array, then the numeric values in element i of the cell array indicate the lags for nonleading exogenous predictor i.

If no predictor lags are used, then this property is empty ([]).

Data Types: double | cell

PreparedCategoricalPredictors — Indices of prepared categorical predictors

positive integer vector | []

This property is read-only.

Indices of the prepared categorical predictors, specified as a positive integer vector. Each index value in PreparedCategoricalPredictors indicates that the corresponding predictor listed in PreparedPredictorNames is categorical. If no prepared predictors are categorical predictors, then this property is empty ([]).

Data Types: double

PreparedPredictorNames — Names of prepared predictors

cell array of character vectors

This property is read-only.

Names of the prepared predictors, specified as a cell array of character vectors. These prepared predictors include variables created from both the predictor variables in X and the response variable Y. Not every predictor is used at every horizon step. To see which predictors are used at a specific horizon step, consult the PreparedPredictorsPerHorizon table.

Data Types: cell

PreparedPredictorsPerHorizon — Prepared predictors at each horizon step

table of logical values

This property is read-only.

Prepared predictors at each horizon step, specified as a table of logical values. Each row of the table corresponds to a horizon step, and each column of the table corresponds to a prepared predictor as listed in PreparedPredictorNames. The logical value in row i and column j indicates whether the software uses prepared predictor j at horizon step i. If the value is 1 (true), then the software uses the predictor. If the value is 0 (false), then the software does not use the predictor.

Data Types: table

PreparedResponseNames — Names of prepared responses at each horizon step

cell array of character vectors

This property is read-only.

Names of the prepared responses at each horizon step, specified as a cell array of character vectors. That is, element i of PreparedResponseNames is the name of the response variable at horizon step i.

For example, given a cross-validated direct forecasting model CVMdl, the name of the response variable at horizon step 1, CVMdl.PreparedResponseNames{1}, matches the response variable name used in the first regression model of each compact direct forecasting model in Learners (such as CVMdl.Learners{1}.Learners{1}.ResponseName).

Data Types: cell

ResponseLags — Response lags used for preparing predictors

positive integer vector | []

This property is read-only.

Response lags used for preparing predictors, specified as a positive integer vector. Each element in ResponseLags indicates the number of time steps by which to shift the response backward in time. The resulting feature is used as a predictor. If no response lags are used, then this property is empty ([]).

Data Types: double

Object Functions

cvloss	Loss for partitioned data at each horizon step
cvpredict	Predict response using cross-validated direct forecasting model

Examples

Evaluate Model Using Expanding Window Cross-Validation

Create a cross-validated direct forecasting model using expanding window cross-validation. To evaluate the performance of the model:

• Compute the mean squared error (MSE) on each test set using the cvloss object function.

• For each test set, compare the true response values to the predicted response values using the cvpredict object function.

Load the sample file TemperatureData.csv, which contains average daily temperature from January 2015 through July 2016. Read the file into a table. Observe the first eight observations in the table.

Tbl = readtable("TemperatureData.csv");
head(Tbl)

    Year       Month       Day    TemperatureF
    ____    ___________    ___    ____________

    2015    {'January'}     1          23     
    2015    {'January'}     2          31     
    2015    {'January'}     3          25     
    2015    {'January'}     4          39     
    2015    {'January'}     5          29     
    2015    {'January'}     6          12     
    2015    {'January'}     7          10     
    2015    {'January'}     8           4     

Create a datetime variable t that contains the year, month, and day information for each observation in Tbl.

numericMonth = month(datetime(Tbl.Month, ...
    InputFormat="MMMM",Locale="en_US"));
t = datetime(Tbl.Year,numericMonth,Tbl.Day);

Plot the temperature values in Tbl over time.

plot(t,Tbl.TemperatureF)
xlabel("Date")
ylabel("Temperature in Fahrenheit")

Create a direct forecasting model by using the data in Tbl. Train the model using a bagged ensemble of trees. All three of the predictors (Year, Month, and Day) are leading predictors because their future values are known. To create new predictors by shifting the leading predictor and response variables backward in time, specify the leading predictor lags and the response variable lags.

Mdl = directforecaster(Tbl,"TemperatureF", ...
    Learner="bag", ...
    LeadingPredictors="all",LeadingPredictorLags={0:1,0:1,0:7}, ...
    ResponseLags=1:7)

Mdl = 
  DirectForecaster

                  Horizon: 1
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: [2]
                 Learners: {[1x1 classreg.learning.regr.CompactRegressionEnsemble]}
                   MaxLag: [7]
          NumObservations: [565]

Mdl is a DirectForecaster model object. By default, the horizon is one step ahead. That is, Mdl predicts a value that is one step into the future.

Partition the time series data in Tbl using an expanding window cross-validation scheme. Create three training sets and three test sets, where each test set has 100 observations. Note that each observation in Tbl is in at most one test set.

CVPartition = tspartition(size(Mdl.X,1),"ExpandingWindow",3, ...
    TestSize=100)

CVPartition = 
  tspartition

               Type: 'expanding-window'
    NumObservations: 565
        NumTestSets: 3
          TrainSize: [265 365 465]
           TestSize: [100 100 100]
           StepSize: 100

The training sets increase in size from 265 observations in the first window to 465 observations in the third window.

Create a cross-validated direct forecasting model using the partition specified in CVPartition. Inspect the Learners property of the resulting CVMdl object.

CVMdl = crossval(Mdl,CVPartition)

CVMdl = 
  PartitionedDirectForecaster

                Partition: [1x1 tspartition]
                  Horizon: 1
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: [2]
                 Learners: {3x1 cell}
                   MaxLag: [7]
          NumObservations: [565]

CVMdl.Learners

ans=3×1 cell array
    {1x1 timeseries.forecaster.CompactDirectForecaster}
    {1x1 timeseries.forecaster.CompactDirectForecaster}
    {1x1 timeseries.forecaster.CompactDirectForecaster}

CVMdl is a PartitionedDirectForecaster model object. The crossval function trains CVMdl.Learners{1} using the observations in the first training set, CVMdl.Learner{2} using the observations in the second training set, and CVMdl.Learner{3} using the observations in the third training set.

Compute the average test set MSE.

averageMSE = cvloss(CVMdl)

averageMSE = 53.3480

To obtain more information, compute the MSE for each test set.

individualMSE = cvloss(CVMdl,Mode="individual")

individualMSE = 3×1

   44.1352
   84.0695
   31.8393

The models trained on the first and third training sets seem to perform better than the model trained on the second training set.

For each test set observation, predict the temperature value using the corresponding model in CVMdl.Learners.

predictedY = cvpredict(CVMdl);
predictedY(260:end,:)

ans=306×1 table
    TemperatureF_Step1
    __________________

             NaN      
             NaN      
             NaN      
             NaN      
             NaN      
             NaN      
          50.963      
          57.363      
           57.04      
          60.705      
          59.606      
          58.302      
          58.023      
           61.39      
          67.229      
          61.083      
      ⋮

Only the last 300 observations appear in any test set. For observations that do not appear in a test set, the predicted response value is NaN.

For each test set, plot the true response values and the predicted response values.

tiledlayout(3,1)

nexttile
idx1 = test(CVPartition,1);
plot(t(idx1),Tbl.TemperatureF(idx1))
hold on
plot(t(idx1),predictedY.TemperatureF_Step1(idx1))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Test Set 1")
hold off

nexttile
idx2 = test(CVPartition,2);
plot(t(idx2),Tbl.TemperatureF(idx2))
hold on
plot(t(idx2),predictedY.TemperatureF_Step1(idx2))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Test Set 2")
hold off

nexttile
idx3 = test(CVPartition,3);
plot(t(idx3),Tbl.TemperatureF(idx3))
hold on
plot(t(idx3),predictedY.TemperatureF_Step1(idx3))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Test Set 3")
hold off

Overall, the cross-validated direct forecasting model is able to predict the trend in temperatures. If you are satisfied with the performance of the cross-validated model, you can use the full DirectForecaster model Mdl for forecasting at time steps beyond the available data.

Evaluate Model Using Holdout Validation

Create a partitioned direct forecasting model using holdout validation. To evaluate the performance of the model:

• At each horizon step, compute the root relative squared error (RRSE) on the test set using the cvloss object function.

• At each horizon step, compare the true response values to the predicted response values using the cvpredict object function.

Load the sample file TemperatureData.csv, which contains average daily temperature from January 2015 through July 2016. Read the file into a table. Observe the first eight observations in the table.

Tbl = readtable("TemperatureData.csv");
head(Tbl)

    Year       Month       Day    TemperatureF
    ____    ___________    ___    ____________

    2015    {'January'}     1          23     
    2015    {'January'}     2          31     
    2015    {'January'}     3          25     
    2015    {'January'}     4          39     
    2015    {'January'}     5          29     
    2015    {'January'}     6          12     
    2015    {'January'}     7          10     
    2015    {'January'}     8           4     

Create a datetime variable t that contains the year, month, and day information for each observation in Tbl.

numericMonth = month(datetime(Tbl.Month, ...
    InputFormat="MMMM",Locale="en_US"));
t = datetime(Tbl.Year,numericMonth,Tbl.Day);

Plot the temperature values in Tbl over time.

plot(t,Tbl.TemperatureF)
xlabel("Date")
ylabel("Temperature in Fahrenheit")

Create a direct forecasting model by using the data in Tbl. Specify the horizon steps as one, two, and three steps ahead. Train a model at each horizon using a bagged ensemble of trees. All three of the predictors (Year, Month, and Day) are leading predictors because their future values are known. To create new predictors by shifting the leading predictor and response variables backward in time, specify the leading predictor lags and the response variable lags.

rng("default")
Mdl = directforecaster(Tbl,"TemperatureF", ...
    Horizon=1:3,Learner="bag", ...
    LeadingPredictors="all",LeadingPredictorLags={0:1,0:1,0:7}, ...
    ResponseLags=1:7)

Mdl = 
  DirectForecaster

                  Horizon: [1 2 3]
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: [2]
                 Learners: {3x1 cell}
                   MaxLag: [7]
          NumObservations: [565]

Mdl is a DirectForecaster model object. Mdl consists of three regression models: Mdl.Learners{1}, which predicts one step ahead; Mdl.Learners{2}, which predicts two steps ahead; and Mdl.Learners{3}, which predicts three steps ahead.

Partition the time series data in Tbl using a holdout validation scheme. Reserve 20% of the observations for testing.

holdoutPartition = tspartition(size(Mdl.X,1),"Holdout",0.20)

holdoutPartition = 
  tspartition

               Type: 'holdout'
    NumObservations: 565
        NumTestSets: 1
          TrainSize: 452
           TestSize: 113

The test set consists of the latest 113 observations.

Create a partitioned direct forecasting model using the partition specified in holdoutPartition.

holdoutMdl = crossval(Mdl,holdoutPartition)

holdoutMdl = 
  PartitionedDirectForecaster

                Partition: [1x1 tspartition]
                  Horizon: [1 2 3]
             ResponseLags: [1 2 3 4 5 6 7]
        LeadingPredictors: [1 2 3]
     LeadingPredictorLags: {[0 1]  [0 1]  [0 1 2 3 4 5 6 7]}
             ResponseName: 'TemperatureF'
           PredictorNames: {'Year'  'Month'  'Day'}
    CategoricalPredictors: [2]
                 Learners: {[1x1 timeseries.forecaster.CompactDirectForecaster]}
                   MaxLag: [7]
          NumObservations: [565]

holdoutMdl is a PartitionedDirectForecaster model object. Because holdoutMdl uses holdout validation rather than a cross-validation scheme, the Learners property of the object contains one CompactDirectForecaster model only.

Like Mdl, holdoutMdl contains three regression models. The crossval function trains holdoutMdl.Learners{1}.Learners{1}, holdoutMdl.Learners{1}.Learners{2}, and holdoutMdl.Learners{1}.Learners{3} using the same training data. However, the three models use different response variables because each model predicts values for a different horizon step.

holdoutMdl.Learners{1}.Learners{1}.ResponseName

ans = 
'TemperatureF_Step1'

holdoutMdl.Learners{1}.Learners{2}.ResponseName

ans = 
'TemperatureF_Step2'

holdoutMdl.Learners{1}.Learners{3}.ResponseName

ans = 
'TemperatureF_Step3'

Compute the root relative squared error (RRSE) on the test data at each horizon step. Use the helper function computeRRSE (shown at the end of this example). The RRSE indicates how well a model performs relative to the simple model, which always predicts the average of the true values. In particular, when the RRSE is less than 1, the model performs better than the simple model.

holdoutRRSE = cvloss(holdoutMdl,LossFun=@computeRRSE)

holdoutRRSE = 1×3

    0.4797    0.5889    0.6103

At each horizon, the direct forecasting model seems to perform better than the simple model.

For each test set observation, predict the temperature value using the corresponding model in holdoutMdl.Learners.

predictedY = cvpredict(holdoutMdl);
predictedY(450:end,:)

ans=116×3 table
    TemperatureF_Step1    TemperatureF_Step2    TemperatureF_Step3
    __________________    __________________    __________________

             NaN                   NaN                   NaN      
             NaN                   NaN                   NaN      
             NaN                   NaN                   NaN      
          41.063                39.758                41.234      
          33.721                36.507                37.719      
          36.987                35.133                37.719      
          38.644                34.598                36.444      
          38.917                34.576                36.275      
          45.888                37.005                 38.34      
          48.516                42.762                 41.05      
          44.882                46.816                43.881      
          35.057                45.301                47.048      
            31.1                41.473                42.948      
          31.817                37.314                42.946      
          33.166                38.419                  41.3      
          40.279                38.432                40.533      
      ⋮

Recall that only the latest 113 observations appear in the test set. For observations that do not appear in the test set, the predicted response value is NaN.

For each test set, plot the true response values and the predicted response values.

tiledlayout(3,1)

idx = test(holdoutPartition);

nexttile
plot(t(idx),Tbl.TemperatureF(idx))
hold on
plot(t(idx),predictedY.TemperatureF_Step1(idx))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Horizon 1")
hold off

nexttile
plot(t(idx),Tbl.TemperatureF(idx))
hold on
plot(t(idx),predictedY.TemperatureF_Step2(idx))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Horizon 2")
hold off

nexttile
plot(t(idx),Tbl.TemperatureF(idx))
hold on
plot(t(idx),predictedY.TemperatureF_Step3(idx))
legend("True Response","Predicted Response", ...
    Location="eastoutside")
xlabel("Date")
ylabel("Temperature")
title("Horizon 3")
hold off

Overall, holdoutMdl is able to predict the trend in temperatures, although it seems to perform best when forecasting one step ahead. If you are satisfied with the performance of the partitioned model, you can use the full DirectForecaster model Mdl for forecasting at time steps beyond the available data.

Helper Function

The helper function computeRRSE computes the RRSE given the true response variable trueY and the predicted values predY. This code creates the computeRRSE helper function.

function rrse = computeRRSE(trueY,predY)
    error = trueY(:) - predY(:);
    meanY = mean(trueY(:),"omitnan");
    rrse = sqrt(sum(error.^2,"omitnan")/sum((trueY(:) - meanY).^2,"omitnan"));
end

More About

Direct Forecasting

Direct forecasting is a forecasting technique that uses separate models to predict the response values at different future time steps (horizon steps). This technique differs from recursive forecasting, where one model is used to predict values at multiple horizon steps.

The software prepares the predictor data for each model and then uses the model to forecast at a particular horizon step.

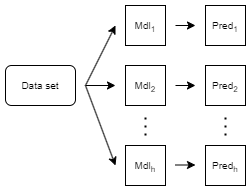
For more information, see PreparedPredictorsPerHorizon and Horizon.

Forecasting Data

The directforecaster function accepts data sets with regularly sampled values that include a response variable and exogenous predictors (optional). That is, the time steps between consecutive observations are the same. In this context, exogenous predictors are predictors that are not derived from the response variable.

Consider the following data set.

In this example, the row times in MeasurementTime show that the time difference between consecutive observations is one hour. The times 18-Dec-2015 14:00:00 and 18-Dec-2015 15:00:00 are future time steps that exist beyond the available data. They represent the first and second horizon steps. (See Horizon.)

Suppose the Temp variable is the response variable. The Pressure, WindSpeed, and WorkHours variables are exogenous predictors. The WorkHours variable is a leading exogenous predictor because its future values are known. (See LeadingPredictors.)

Before fitting a forecasting model, the software creates time-shifted features from the response and exogenous predictors based on user-specified lag values. In this example, the red rectangles indicate a ResponseLags value of 1, PredictorLags value of [1 2 3], and LeadingPredictorLags value of [0 1] at horizon step 1 (18-Dec-2015 14:00:00).

Version History

Introduced in R2023b