cwtft2
2-D continuous wavelet transform
Description
Examples
Load and display the star image.
img = imread("star.jpg");
image(img)
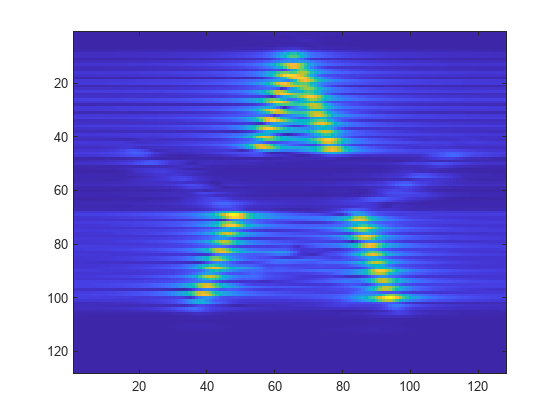
Obtain the 2-D CWT of the star image using the default function values. Visualize the magnitudes of the coefficients at the finest scale.
cwtout = cwtft2(img); sca = 1; imagesc(abs(cwtout.cfs(:,:,1,1,sca)))
This example shows how an isotropic wavelet does not discern the orientation of features while an anisotropic wavelet does. In the example, you use the Marr isotropic wavelet and the directional (anisotropic) Cauchy wavelet.
Load and view the hexagon image.
img = imread("hexagon.jpg");
imagesc(img)
Obtain the 2-D CWT of the image using both the Marr and Cauchy wavelets. Specify a scale equal to 1. Specify a vector of angles going from 0 to radians in increments.
cwtScales = 1; cwtAngles = 0:pi/8:2*pi-pi/8; cwtCauchy = cwtft2(img,wavelet="cauchy",scales=cwtScales, ... angles=cwtAngles); cwtMarr = cwtft2(img,wavelet="marr",scales=cwtScales, ... angles=cwtAngles);
There are 16 angles. Visualize the scale-one 2-D CWT coefficient magnitudes at any two consecutive angles. Confirm that using the Marr isotropic wavelet does not discern the orientation of features, but the Cauchy wavelet does.
angz = {"0", "pi/8", "pi/4", "3pi/8", "pi/2", "5pi/8", "3pi/4", ...
"7pi/8","pi", "9pi/8", "5pi/4", "11pi/8", "3pi/2", ...
"13pi/8" "7pi/4", "15pi/8"};
indexAngle1 = 7;
indexAngle2 = 8;
tiledlayout(2,2)
for k=[indexAngle1 indexAngle2]
nexttile
imagesc(abs(cwtMarr.cfs(:,:,1,1,k)))
title(["Marr Wavelet at " angz(k) "radians"])
nexttile
imagesc(abs(cwtCauchy.cfs(:,:,1,1,k)))
title(["Cauchy Wavelet at " angz(k) "radians"])
end
Visualize the 2-D CWT coefficient magnitudes obtained using the Marr isotropic wavelet at any two angles. Confirm the wavelet does not discern the orientation of features.
indexAngle1 = 2; indexAngle2 = 7; tiledlayout(1,2) for k=[indexAngle1 indexAngle2] nexttile imagesc(abs(cwtMarr.cfs(:,:,1,1,k))) title(["Marr Wavelet at " angz(k) "radians"]) end

Input Arguments
Input data, specified as a numeric array. X can be an
M-by-N array representing an
indexed image or an M-by-N-by-3 array
representing a truecolor image.
Data Types: double | single | uint8 | uint16
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: wavelet="paul",scales=2.^(0:5) specifies the Paul
wavelet and a vector of scales.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: "wavelet","paul","scales",2.^(0:5) specifies the Paul wavelet and a
vector of scales.
Angles in radians used in the 2-D CWT, specified as a scalar or a vector.
Example: angles=[0 pi/2 pi]
Normalization to use in the 2-D CWT, specified as one of these:
"L2"— The Fourier transform of the analyzing wavelet at a given scale is multiplied by the corresponding scale."L2"is the default normalization."L1"— The Fourier transform of the analyzing wavelet is multiplied by 1 at all scales."L0"— The Fourier transform of the analyzing wavelet at a given scale is multiplied by the square of the corresponding scale.
Example: norm="L1"
Scales to use in the 2-D CWT, specified as a real-valued scalar or vector. Scales must be greater than or equal to 1.
Example: scales=[1 2 3 5 8]
Data Types: double | single
Analyzing wavelet, specified as a character vector, a string scalar, a structure, or a cell
array. cwtftinfo2 provides a
comprehensive list of supported wavelets and associated
parameters.
If you specify wavelet as a structure, the structure must contain two fields:
name— Character vector or string scalar corresponding to a supported wavelet.param— Cell array containing optional parameters, which depend on the wavelet. If you do not wish to specify optional parameters, use an empty cell array in the field.
If you specify wavelet as a cell array, wav, the cell
array must contain two elements:
wav{1}— Character vector or string scalar corresponding to a supported wavelet.wav{2}— Cell array with the parameters of the wavelet.
Example: wavelet={"morlet",{6,1,1}} specifies the Morlet wavelet as a cell
array.
Example: wavelet=struct("name","paul","param",{{2}}) specifies the Paul
wavelet as a structure array.
Output Arguments
The 2-D CWT, returned as a structure with the following fields:
Analyzing wavelet and parameters, returned as a structure with the following fields:
wname— Wavelet nameparam— Wavelet parameters
Normalization constants, returned as an M-by-N matrix, where M is the number of scales and N is the number of angles.
CWT coefficients, returned as an N-D array.
The row and column dimensions of the array equal the row and column dimensions of the input data.
The third page of the array is equal to 1 or 3, depending on whether the input data is a grayscale or truecolor image, respectively.
The fourth page of the array is equal to the number of scales.
The fifth page of the array is equal to the number of angles.
Scales for the 2-D CWT, returned as a row vector.
Angles for the 2-D CWT, returned as a row vector.
Mean of the input data, returned as a scalar.
Algorithms
The cwtft2 function uses a Fourier transform-based algorithm in
which the 2-D Fourier transforms of the input data and analyzing wavelet are multiplied
together and inverted.
Extended Capabilities
Usage notes and limitations:
The value of the
waveletname-value argument must be constant at compile time. Usecoder.Constant(MATLAB Coder).Plotting is not supported.
Version History
Introduced in R2013bThe cwtft2 function supports C/C++ code generation. You must
have MATLAB®
Coder™ to generate C/C++ code.
You can use the cwtft2 function to obtain the 2-D CWT of a
16-bit image.
The plotting syntax for the cwtft2 function continues to
work, but is no longer recommended. Use the Wavelet Image
Analyzer app instead.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)