Change the Bandwidth of a HAC Estimator
This example shows how to change the bandwidth when estimating a HAC coefficient covariance, and compare estimates over varying bandwidths and kernels.
How does the bandwidth affect HAC estimators? If you change it, are there large differences in the estimates, and, if so, are the differences practically significant? Explore bandwidth effects by estimating HAC coefficient covariances over a grid of bandwidths.
Load and Plot Data
Determine how the cost of living affects the behavior of nominal wages. Load the Nelson Plosser data set to explore their statistical relationship.
load Data_NelsonPlosser DTT = rmmissing(DataTimeTable); cpi = DTT.CPI; % Cost of living wm = DTT.WN; % Nominal wages figure plot(DTT.CPI,DTT.WN,"o") hFit = lsline; % Regression line xlabel("Consumer Price Index (1967 = 100)") ylabel("Nominal Wages (current $)") legend(hFit,"OLS Line",Location="southeast") title("{\bf Cost of Living}") grid on
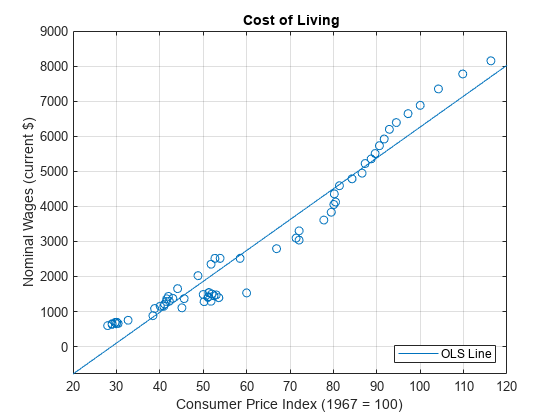
The plot suggests that a linear model might capture the relationship between the two variables.
Define Model
Model the behavior of nominal wages with respect to CPI as this linear model.
Mdl = fitlm(DTT.CPI,DTT.WN)
Mdl =
Linear regression model:
y ~ 1 + x1
Estimated Coefficients:
Estimate SE tStat pValue
________ ______ _______ _________
(Intercept) -2541.5 174.64 -14.553 2.407e-21
x1 88.041 2.6784 32.871 4.507e-40
Number of observations: 62, Error degrees of freedom: 60
Root Mean Squared Error: 494
R-squared: 0.947, Adjusted R-Squared: 0.947
F-statistic vs. constant model: 1.08e+03, p-value = 4.51e-40
coeffCPI = Mdl.Coefficients.Estimate(2); seCPI = Mdl.Coefficients.SE(2);
Plot Residuals
Plot the residuals from Mdl against the fitted values to assess heteroscedasticity and autocorrelation.
figure stem(Mdl.Residuals.Raw) xlabel("Observation") ylabel("Residual") title("{\bf Linear Model Residuals}") axis tight grid on
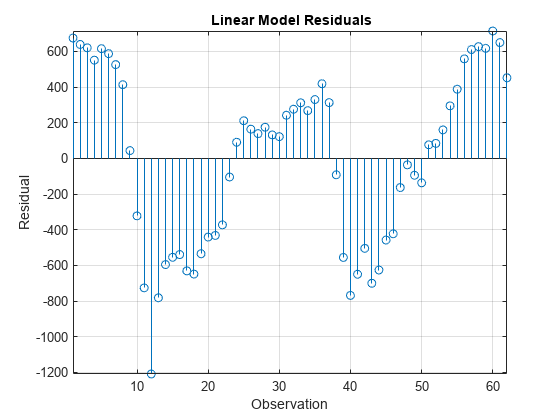
The residual plot shows varying levels of dispersion, which indicates heteroscedasticity. Neighboring residuals (with respect to observation) tend to have the same sign and magnitude, which indicates the presence of autocorrelation.
Estimate HAC standard errors.
Obtain HAC standard errors over varying bandwidths using the Bartlett (for the Newey-West estimate) and quadratic spectral kernels.
numEstimates = 10; stdErrBT = zeros(numEstimates,1); stdErrQS = zeros(numEstimates,1); for bw = 1:numEstimates [~,CoeffTbl] = hac(DTT,ResponseVariable="WN",PredictorVariables="CPI", ... Bandwidth=bw,Display="off"); % Newey-West [~,CoeffTblQS] = hac(DTT,ResponseVariable="WN",PredictorVariables="CPI", ... Weights="QS",Bandwidth=bw,Display="off"); % HAC using quadratic spectral kernel stdErrBT(bw) = CoeffTbl.SE(2); stdErrQS(bw) = CoeffTblQS.SE(2); end
You can increase numEstimates to discover how increasing bandwidths affect the HAC estimates.
Plot Standard Errors
Visually compare the Newey-West standard errors of to those using the quadratic spectral kernel over the bandwidth grid.
figure hold on hCoeff = plot(1:numEstimates,repmat(coeffCPI,numEstimates,1), ... LineWidth=2); hOLS = plot(1:numEstimates,repmat(coeffCPI+seCPI,numEstimates,1), ... "g--"); plot(1:numEstimates,repmat(coeffCPI-seCPI,numEstimates,1),"g--") hBT = plot(1:numEstimates,coeffCPI+stdErrBT,"ro--"); plot(1:numEstimates,coeffCPI-stdErrBT,"ro--") hQS = plot(1:numEstimates,coeffCPI+stdErrQS,"kp--", ... LineWidth=2); plot(1:numEstimates,coeffCPI-stdErrQS,"kp--",LineWidth=2) hold off xlabel("Bandwidth") ylabel("CPI Coefficient") legend([hCoeff,hOLS,hBT,hQS],["OLS estimate" "OLS SE" ... "Newey-West SE" "Quadratic spectral SE"],Location="east") title("{\bf CPI Coefficient Standard Errors}") grid on
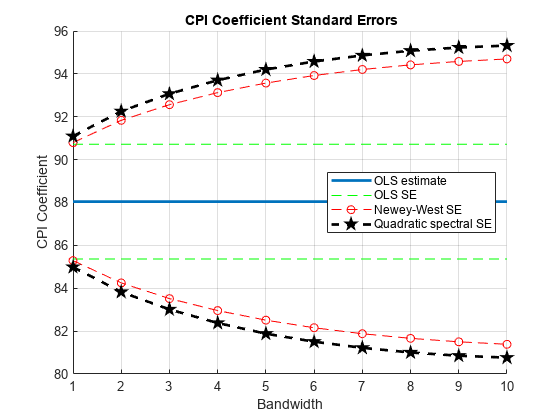
The plot suggests that, for this data set, accounting for heteroscedasticity and autocorrelation using either HAC estimate results in more conservative intervals than the usual OLS standard error. The precision of the HAC estimates decreases as the bandwidth increases along the defined grid.
For this data set, the Newey-West estimates are slightly more precise than those using the quadratic spectral kernel. This might be because the latter captures heteroscedasticity and autocorrelation better than the former.
References:
Andrews, D. W. K. "Heteroskedasticity and Autocorrelation Consistent Covariance Matrix Estimation." Econometrica. Vol. 59, 1991, pp. 817-858.
Newey, W. K., and K. D. West. "A Simple, Positive Semi-definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix." Econometrica. Vol. 55, No. 3, 1987, pp. 703-708.\
Newey, W. K., and K. D. West. "Automatic Lag Selection in Covariance Matrix Estimation." The Review of Economic Studies. Vol. 61, No. 4, 1994, pp. 631-653.