simulate
Simulate sample paths of threshold-switching dynamic regression model
Since R2021b
Description
Y = simulate(Mdl,numObs,Name,Value)simulate(Mdl,10,NumPaths=1000,Y0=Y0) simulates
1000 sample paths of length 10, and initializes the
dynamic component of each submodel by using the presample response data
Y0.
[
also returns the simulated innovation paths Y,E,StatePaths] = simulate(___)E and the simulated state
paths StatePaths, using any of the input argument combinations in the
previous syntaxes.
Examples
Suppose a data-generating process (DGP) is a two-state, self-exciting threshold autoregressive (SETAR) model for a 1-D response variable. Specify all parameter values (this example uses arbitrary values).
Create Fully Specified Model for DGP
Create a discrete threshold transition at level 0. Label the regimes to reflect the state of the economy:
When the threshold variable (currently unknown) is in , the economy is in a recession.
When the threshold variable is in , the economy is expanding.
t = 0; tt = threshold(t,StateNames=["Recession" "Expansion"])
tt =
threshold with properties:
Type: 'discrete'
Levels: 0
Rates: []
StateNames: ["Recession" "Expansion"]
NumStates: 2
tt is a fully specified threshold object that describes the switching mechanism of the threshold-switching model.
Assume the following univariate models describe the response process of the system:
Recession: , where .
Expansion: , where .
For each regime, use arima to create an AR model that describes the response process within the regime.
c1 = -1; c2 = 1; ar1 = 0.1; ar2 = [0.3 0.2]; v1 = 1; v2 = 4; mdl1 = arima(Constant=c1,AR=ar1,Variance=v1,... Description="Recession State Model")
mdl1 =
arima with properties:
Description: "Recession State Model"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 1
D: 0
Q: 0
Constant: -1
AR: {0.1} at lag [1]
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: 1
ARIMA(1,0,0) Model (Gaussian Distribution)
mdl2 = arima(Constant=c2,AR=ar2,Variance=v2,... Description="Expansion State Model")
mdl2 =
arima with properties:
Description: "Expansion State Model"
SeriesName: "Y"
Distribution: Name = "Gaussian"
P: 2
D: 0
Q: 0
Constant: 1
AR: {0.3 0.2} at lags [1 2]
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: 4
ARIMA(2,0,0) Model (Gaussian Distribution)
mdl1 and mdl2 are fully specified arima objects.
Store the submodels in a vector with order corresponding to the regimes in tt.StateNames.
mdl = [mdl1; mdl2];
Use tsVAR to create a TAR model from the switching mechanism tt and the state-specific submodels mdl.
Mdl = tsVAR(tt,mdl)
Mdl =
tsVAR with properties:
Switch: [1×1 threshold]
Submodels: [2×1 varm]
NumStates: 2
NumSeries: 1
StateNames: ["Recession" "Expansion"]
SeriesNames: "1"
Covariance: []
Mdl.Submodels(2)
ans =
varm with properties:
Description: "AR-Stationary 1-Dimensional VAR(2) Model"
SeriesNames: "Y1"
NumSeries: 1
P: 2
Constant: 1
AR: {0.3 0.2} at lags [1 2]
Trend: 0
Beta: [1×0 matrix]
Covariance: 4
Mdl is a fully specified tsVAR object representing a univariate two-state TAR model. tsVAR stores specified arima submodels as varm objects.
Simulate Response Data from DGP
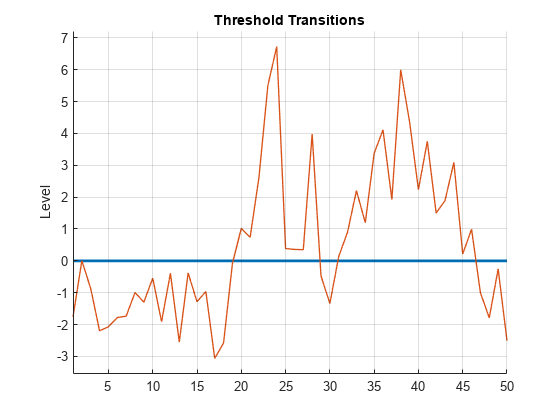
Generate one random response path of length 50 from the model. simulate assumes that the threshold variable is , which implies that the model is self-exciting.
rng(1); % For reproducibility
y = simulate(Mdl,50);y is a 50-by-1 vector of one response path.
Plot the response path with the threshold by using ttplot.
figure ttplot(Mdl.Switch,Data=y)
Consider the following logistic TAR (LSTAR) model for the annual, CPI-based, Canadian inflation rate series .
State 1: , where
State 2: , where
State 3: , where
The system is in state 1 when , the system is in state 2 when , and the system is in state 3 otherwise.
The transition function rate between states 1 and 2 is 3.5, and the transition function rate between states 2 and 3 is 1.5.
Create an LSTAR model representing .
t = [2 8];
tt = threshold([2 8],Type="logistic",Rates=[3.5 1.5]);
mdl1 = arima(Constant=-5,Variance=0.1);
mdl2 = arima(Constant=0,Variance=0.2);
mdl3 = arima(Constant=5,Variance=0.3);
Mdl = tsVAR(tt,[mdl1; mdl2; mdl3]);Load the Canadian inflation and interest rate data set.
load Data_CanadaExtract the CPI-based inflation rate series.
INF_C = DataTable.INF_C; numObs = length(INF_C);
Simulate ten paths from the model. Specify the threshold variable type and its data.
Y = simulate(Mdl,numObs,NumPaths=10,Type="exogenous",Z=INF_C);Y is a numObs-by-10 matrix of simulated paths. Each column represents an independently simulated path.
In a tiled layout, plot the threshold transitions with the data by using ttplot,and plot the simulated paths to one tile.
tiledlayout(2,1) nexttile ttplot(tt,Data=INF_C) colorbar('off') xticklabels(dates(xticks)) nexttile plot(dates,Y) grid on axis tight title("Simulations")

Y switches between submodels according to the value of the threshold variable INF_C. Mixing is evident for observations near thresholds, such as at the inflation rates of 1964 and 1978.
Consider the model for the annual, CPI-based, Canadian inflation rate series in Simulate Multiple Paths.
Create the LSTAR model for the series.
t = [2 8];
tt = threshold([2 8],Type="logistic",Rates=[3.5 1.5]);
mdl1 = arima(Constant=-5,Variance=0.1);
mdl2 = arima(Constant=0,Variance=0.2);
mdl3 = arima(Constant=5,Variance=0.3);
Mdl = tsVAR(tt,[mdl1; mdl2; mdl3]);Load the Canadian inflation and interest rate data set and extract the inflation rate series.
load Data_Canada
INF_C = DataTable.INF_C;
numObs = length(INF_C);Simulate a length numObs path from the model. Specify the threshold variable type and its data. Return the innovations and states.
[y,e,s] = simulate(Mdl,numObs,NumPaths=10,Type="exogenous",Z=INF_C); tiledlayout(3,1) nexttile plot(y); ylabel("Simulated Response") grid on nexttile plot(e) ylabel('Innovation') grid on nexttile stem(s) ylabel('State') yticks([1 2 3]) yticklabels(Mdl.StateNames)

This example shows how to initialize simulated paths from presample responses and initial states. The example uses arbitrary parameter values.
Fully Specify LSETAR Model
Consider the following 2-D LSETAR model.
State 1,
"Low": whereState 2 ,
"Med": whereState 3,
"High": whereThe system is in state 1 when , the system is in state 2 when , and the system is in state 3 otherwise.
The transition function is logistic. The transition rate from state 1 to 2 is 3.5, and the transition rate from state 1 to 3 is 1.5.
Create logistic threshold transitions at mid-levels -1 and 1 with rates 3.5 and 1.5, respectively. Label the states.
t = [-1 1]; r = [3.5 1.5]; stateNames = ["Low" "Med" "High"]; tt = threshold(t,Type="logistic",Rates=[3.5 1.5],StateNames=stateNames);
Create the VAR submodels by using varm. Store the submodels in a vector with order corresponding to the regimes in tt.StateNames.
% Constants (numSeries x 1 vectors) C1 = [1; -1]; C2 = [2; -2]; C3 = [3; -3]; % Autoregression coefficients (numSeries x numSeries matrices) AR1 = {}; % 0 lags AR2 = {[0.5 0.1; 0.5 0.5]}; % 1 lag AR3 = {[0.25 0; 0 0] [0 0; 0.25 0]}; % 2 lags % Innovations covariances (numSeries x numSeries matrices) Sigma1 = [1 -0.1; -0.1 1]; Sigma2 = [2 -0.2; -0.2 2]; Sigma3 = [3 -0.3; -0.3 3]; % VAR Submodels mdl1 = varm('Constant',C1,'AR',AR1,'Covariance',Sigma1); mdl2 = varm('Constant',C2,'AR',AR2,'Covariance',Sigma2); mdl3 = varm('Constant',C3,'AR',AR3,'Covariance',Sigma3); mdl = [mdl1; mdl2; mdl3];
Create an LSETAR model from the switching mechanism tt and the state-specific submodels mdl. Label the series Y1 and Y2.
Mdl = tsVAR(tt,mdl,SeriesNames=["Y1" "Y2"])
Mdl =
tsVAR with properties:
Switch: [1×1 threshold]
Submodels: [3×1 varm]
NumStates: 3
NumSeries: 2
StateNames: ["Low" "Med" "High"]
SeriesNames: ["Y1" "Y2"]
Covariance: []
Mdl is a fully specified tsVAR object representing a multivariate three-state LSETAR model. tsVAR object functions enable you to specify threshold variable characteristics and data.
Initialize Simulation from Presample Responses
Consider simulating 5 paths initialized from presample responses. Specify a numPreObs-by-numSeries-by-numPaths array of presample responses, where:
numPreObsis the number of presample responses per series and path. You must specify enough presample observations to initialize all AR components in the VAR models and the endogenous threshold variable. The largest AR component order is 2 and the threshold variable delay is 4, thereforesimulaterequiresnumPreObs=4presample observations per series and path.numSeries=2, the number of response series in the system.numPaths=5, the number of independent paths to simulate.
delay = 4; numPaths = 5; Y0 = zeros(delay,Mdl.NumSeries,numPaths); for j = 2:numPaths Y0(:,:,j) = 10*j*ones(delay,Mdl.NumSeries); end
Simulate 10 paths of length 100 from the LSETAR model from the presample. Specify the endogenous threshold variable and its delay, .
numObs = 100; rng(1); Y = simulate(Mdl,numObs,NumPaths=numPaths,Y0=Y0,Index=2,Delay=4);
Y is a 100-by-2-by-5 array of simulate response paths. For example, Y(50,2,3) is the simulated response of path 3, of series Y2, at time point 50.
Plot the simulated paths for each variable on separate plots.
tiledlayout(2,1) nexttile plot(squeeze(Y(:,1,:))) title("Y1") nexttile plot(squeeze(Y(:,2,:))) title("Y2")

The system quickly settles regardless of the presample.
Initialize Simulation from States
Simulate three paths of length 100, where each of the three states initialize a path. Specify state indices for initialization, and specify the endogenous threshold variable and its delay.
S0 = 1:Mdl.NumStates; numPaths = numel(S0); Y = simulate(Mdl,numObs,NumPaths=numPaths,S0=S0,Index=2,Delay=4); tiledlayout(2,1) nexttile plot(squeeze(Y(:,1,:))) title("Y1") nexttile plot(squeeze(Y(:,2,:))) title("Y2")

Consider including regression components for exogenous variables in each submodel of the threshold-switching dynamic regression model in Initialize Multivariate Model Simulation from Multiple Starting Conditions.
Fully Specify LSETAR Model
Create logistic threshold transitions at mid-levels -1 and 1 with rates 3.5 and 1.5, respectively. Label the states.
t = [-1 1]; r = [3.5 1.5]; stateNames = ["Low" "Med" "High"]; tt = threshold(t,Type="logistic",Rates=[3.5 1.5],StateNames=stateNames)
tt =
threshold with properties:
Type: 'logistic'
Levels: [-1 1]
Rates: [3.5000 1.5000]
StateNames: ["Low" "Med" "High"]
NumStates: 3
Assume the following VARX models describe the response processes of the system:
State 1: where
State 2: where
State 3: where
represents a single exogenous variable, represents two exogenous variables, and represents three exogenous variables. Store the submodels in a vector.
% Constants (numSeries x 1 vectors) C1 = [1; -1]; C2 = [2; -2]; C3 = [3; -3]; % Regression coefficients (numSeries x numRegressors matrices) Beta1 = [1; -1]; % 1 regressor Beta2 = [2 2; -2 -2]; % 2 regressors Beta3 = [3 3 3; -3 -3 -3]; % 3 regressors % Autoregression coefficients (numSeries x numSeries matrices) AR1 = {}; AR2 = {[0.5 0.1; 0.5 0.5]}; AR3 = {[0.25 0; 0 0] [0 0; 0.25 0]}; % Innovations covariances (numSeries x numSeries matrices) Sigma1 = [1 -0.1; -0.1 1]; Sigma2 = [2 -0.2; -0.2 2]; Sigma3 = [3 -0.3; -0.3 3]; %VARX submodels mdl1 = varm(Constant=C1,AR=AR1,Beta=Beta1,Covariance=Sigma1); mdl2 = varm(Constant=C2,AR=AR2,Beta=Beta2,Covariance=Sigma2); mdl3 = varm(Constant=C3,AR=AR3,Beta=Beta3,Covariance=Sigma3); mdl = [mdl1; mdl2; mdl3];
Create an LSETAR model from the switching mechanism tt and the state-specific submodels mdl. Label the series Y1 and Y2.
Mdl = tsVAR(tt,mdl,SeriesNames=["Y1" "Y2"])
Mdl =
tsVAR with properties:
Switch: [1×1 threshold]
Submodels: [3×1 varm]
NumStates: 3
NumSeries: 2
StateNames: ["Low" "Med" "High"]
SeriesNames: ["Y1" "Y2"]
Covariance: []
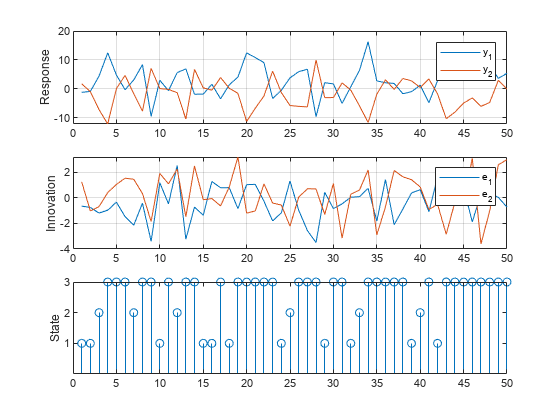
Simulate Data Ignoring Regression Component
If you do not supply exogenous data, simulate ignores the regression components in the submodels. Simulate a single path of responses, innovations, and states into a simulation horizon of length 50. Then plot each path separately.
rng(1); % For reproducibility numObs = 50; [Y,E,SP] = simulate(Mdl,numObs); figure tiledlayout(3,1) nexttile plot(Y) ylabel("Response") grid on legend(["y_1" "y_2"]) nexttile plot(E) ylabel("Innovation") grid on legend(["e_1" "e_2"]) nexttile stem(SP) ylabel("State") yticks([1 2 3])

Simulate Data Including Regression Component
simulate requires exogenous data in order to generate random paths from the model. Simulate exogenous data for the three regressors by generating 50 random observations from the 3-D standard Gaussian distribution.
X = randn(50,3);
Generate one random response, innovation, and state path of length 50. Specify the simulated exogenous data for the submodel regression components. Plot the results.
rng(1); % Reset seed for comparison [Y,E,SP] = simulate(Mdl,numObs,X=X); figure tiledlayout(3,1) nexttile plot(Y) ylabel("Response") grid on legend(["y_1" "y_2"]) nexttile plot(E) ylabel("Innovation") grid on legend(["e_1" "e_2"]) nexttile stem(SP) ylabel("State") yticks([1 2 3])
This example shows how to use Monte Carlo estimation to obtain an interval estimate of the threshold mid-level.
Consider a SETAR model for the real US GDP growth rate with AR(4) submodels. Suppose the threshold variable is (self exciting with 0 delay).
Create a discrete threshold transition at unknown mid-level . Label the states "Recession" and "Expansion".
tt = threshold(NaN,StateNames=["Recession" "Expansion"]);
For each state, create a partially specified AR(4) model with one coefficient at lag 4. Store the state submodels in a vector.
submdl = arima(ARLags=4); mdl = [submdl; submdl];
Each submodel has an unknown, estimable lag 4 coefficient, model constant, and innovations variance.
Create a partially specified TAR model from the threshold transition and submodel vector.
Mdl = tsVAR(tt,mdl);
Create a fully specified threshold transition that has the same structure as tt, but set the mid-level to 0.
tt0 = threshold(0);
Load the US macroeconomic data set. Compute the real GDP growth rate as a percent.
load Data_USEconModel
rGDP = DataTimeTable.GDP./DataTimeTable.GDPDEF;
pRGDP = 100*price2ret(rGDP);
T = numel(pRGDP);Fit the TAR to the real GDP rate series.
EstMdl = estimate(Mdl,tt0,pRGDP,Z=pRGDP,Type="exogenous");Simulate 100 response paths from the estimated model.
rng(100) % For reproducibility numPaths= 100; Y = simulate(EstMdl,T,NumPaths=numPaths,Z=pRGDP,Type="exogenous");
Fit the TAR model to each simulated response path. Specify the estimated threshold transition EstMdl.Switch to initialize the estimation procedure. For each path, store the estimated threshold transition mid-level.
tMC = nan(T,1); for j = 1:numPaths EstMdlSim = estimate(Mdl,EstMdl.Switch,Y(:,j),Z=Y(:,j),Type="exogenous"); tMC(j) = EstMdlSim.Switch.Levels; end
tMC is a 100-by-1 vector representing a Monte Carlo sample of threshold transitions.
Obtain a 95% confidence interval on the true threshold transition by computing the 0.25 and .975 quantiles of the Monte Carlo sample.
tCI = quantile(tMC,[0.025 0.975])
tCI = 1×2
0.5158 0.9810
A 95% confidence interval on the true threshold transition is (0.52%, 0.98%).
Input Arguments
Number of observations to generate for each sample path, specified as a positive integer.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: NumPaths=1000,Y0=Y0 simulates 1000 sample
paths and initializes the dynamic component of each submodel by using the presample response
data Y0.
Number of sample paths to generate, specified as a positive integer.
Example: NumPaths=1000
Data Types: double
Type of threshold variable data, specified as a value in this table.
| Value | Description |
|---|---|
"endogenous" | The model is self-exciting with threshold variable data generated by response j, where
|
"exogenous" | The threshold variable is exogenous to the system. The name-value argument 'Z' specifies the threshold variable data and is required. |
Example: Type="exogenous",Z=z specifies the data z for the exogenous threshold variable.
Example: Type="endogenous",Index=2,Delay=4 specifies the endogenous threshold variable as y2,t−4, whose data is Y(:,2).
Data Types: char | string | cell
Presample response data, specified as a numeric matrix or array.
To use the same presample data for each of the numPaths path,
specify a numPreSampleObs-by-numSeries matrix,
where numPaths is the value of NumPaths,
numPreSampleObs is the number of presample observations, and
numSeries is the number of response variables.
To use different presample data for each path:
For univariate ARX submodels, specify a
numPreSampleObs-by-numPathsmatrix.For multivariate VARX submodels, specify a
numPreSampleObs-by-numSeries-by-numPathsarray.
The number of presample observations numPreSampleObs must be
sufficient to initialize the AR terms of all submodels. For models of type
"endogenous", the number of presample observations must also be
sufficient to initialize the delayed response. If numPreSampleObs
exceeds the number necessary to initial the model, simulate
uses only the latest observations. The last row contains the latest observations.
simulate updates Y0 using the latest
simulated observations each time it switches states.
By default, simulate determines Y0 by
the submodel of the initial state:
If the initial submodel is a stationary AR process without regression components,
simulatesets presample observations to the unconditional mean.Otherwise,
simulatesets presample observations to zero.
Data Types: double
Threshold variable data for simulations of type "exogenous",
specified as a numeric vector of length numObsZ or a
numObsZ-by-numPaths numeric matrix.
For a numeric vector, simulate applies the same data to
all simulated paths. For a matrix, simulate applies columns of
Z to corresponding simulated paths.
If numObsZ exceeds numobs,
simulate uses only the latest observations. The last row
contains the latest observation.
simulate determines the initial state of simulations by
values in the first row Z(1,:).
Data Types: double
Threshold variable delay d in
yj,t−d
for simulations of type "endogenous", specified as a positive
integer.
Example: Delay=4 specifies that the threshold variable is
y2,t−d,
where j is the value of Index.
Data Types: double
Threshold variable index j in
yj,t−d
for simulations of type "endogenous", specified as a scalar in
1:Mdl.NumSeries.
simulate ignores Index for univariate
AR models.
Example: Index=2 specifies that the threshold variable is
y2,t−d,
where d is the value of Delay.
Data Types: double
Initial states of simulations, for simulations of type
"endogenous", specified as a numeric scalar or vector of length
numPaths. Entries of S0 must be in
1:Mdl.NumStates.
A scalar S0 applies the same initial state to all paths. A
vector S0 applies initial state
S0( to path
j)j
If you specify Y0, simulate ignores
S0 and determines initial states by the specified presample
data.
Example: 'S0',2 applies state 2 to initialize
all paths.
Example: 'S0',[2 3] specifies state 2 as the initial
state.
Data Types: double
Predictor data used to evaluate regression components in all submodels of
Mdl, specified as a numeric matrix or a cell vector of numeric
matrices.
To use a subset of the same predictors in each state, specify X
as a matrix with numPreds columns and at least
numObs rows. Columns correspond to distinct predictor variables.
Submodels use initial columns of the associated matrix, in order, up to the number of
submodel predictors. The number of columns in the Beta property of
Mdl.SubModels( determines the
number of exogenous variables in the regression component of submodel
j)jnumObs, then simulate uses the latest
observations.
To use different predictors in each state, specify a cell vector of such matrices
with length numStates.
By default, simulate ignores regression components in
Mdl.
Data Types: double
Output Arguments
Simulated response paths, returned as a numeric matrix or array. Y represents the continuation of the presample responses in Y0.
For univariate ARX submodels, Y is a numObs-by-numPaths matrix. For multivariate VARX submodels, Y is a numObs-by-numSeries-by-numPaths array.
Simulated innovation paths, returned as a numeric matrix or array.
For univariate ARX submodels, E is a
numObs-by-numPaths matrix. For multivariate VARX
submodels, E is a
numObs-by-numSeries-by-numPaths
array.
simulate generates innovations using the covariance
specification in Mdl. For more details, see tsVAR.
Simulated state paths, returned as a
numObs-by-numPaths numeric matrix.
If threshold levels in Mdl.Switch.Levels are
t1,
t2,…
,tn,
simulate labels states of the threshold variable
(-∞,t1),
[t1,t2),
… [tn,∞) as 1,
2, 3,... n + 1, respectively.
References
[1] Teräsvirta, Tima. "Modelling Economic Relationships with Smooth Transition Regressions." In A. Ullahand and D.E.A. Giles (eds.), Handbook of Applied Economic Statistics, 507–552. New York: Marcel Dekker, 1998.
[2] van Dijk, Dick. Smooth Transition Models: Extensions and Outlier Robust Inference. Rotterdam, Netherlands: Tinbergen Institute Research Series, 1999.
Version History
Introduced in R2021b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Seleccione un país/idioma
Seleccione un país/idioma para obtener contenido traducido, si está disponible, y ver eventos y ofertas de productos y servicios locales. Según su ubicación geográfica, recomendamos que seleccione: .
También puede seleccionar uno de estos países/idiomas:
Cómo obtener el mejor rendimiento
Seleccione China (en idioma chino o inglés) para obtener el mejor rendimiento. Los sitios web de otros países no están optimizados para ser accedidos desde su ubicación geográfica.
América
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)