Optimizar funciones no lineales
Minimizar funciones de una variable
Dada una función matemática de una única variable, puede utilizar la función fminbnd para encontrar un minimizador local de la función en un intervalo determinado. Por ejemplo, considere la función humps.m que se proporciona con MATLAB®. La siguiente figura muestra la gráfica de humps.
x = -1:.01:2; y = humps(x); plot(x,y) xlabel('x') ylabel('humps(x)') grid on

Para encontrar el mínimo de la función humps en el intervalo (0.3,1), utilice
x = fminbnd(@humps,0.3,1)
x = 0.6370
Puede ver los detalles del proceso de solución utilizando optimset para crear opciones con la opción Display establecida en 'iter'. Pase las opciones resultantes a fminbnd.
options = optimset('Display','iter'); x = fminbnd(@humps,0.3,1,options)
Func-count x f(x) Procedure
1 0.567376 12.9098 initial
2 0.732624 13.7746 golden
3 0.465248 25.1714 golden
4 0.644416 11.2693 parabolic
5 0.6413 11.2583 parabolic
6 0.637618 11.2529 parabolic
7 0.636985 11.2528 parabolic
8 0.637019 11.2528 parabolic
9 0.637052 11.2528 parabolic
Optimization terminated:
the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04
x = 0.6370
La visualización iterativa muestra el valor actual de x y el valor de función en f(x) cada vez que se produce una evaluación de función. Para fminbnd, una evaluación de función corresponde a una iteración del algoritmo. La última columna muestra el procedimiento que utiliza fminbnd en cada iteración, una búsqueda de sección áurea o una interpolación parabólica. Para obtener más detalles, consulte Optimization Solver Iterative Display.
Nota: Los solvers de optimización se aplican a funciones con valor real. Los valores complejos no se pueden optimizar, excepto para una función con valor real de los valores complejos, como la norma.
Minimizar funciones de varias variables
La función fminsearch es similar a fminbnd, con la excepción de que resuelve funciones de muchas variables. Especifique un vector de inicio x0 en lugar de un intervalo de inicio. fminsearch intenta devolver un vector x que es un minimizador local de la función matemática cercana a este vector de inicio.
Para probar fminsearch, cree una función three_var de tres variables, x, y y z.
function b = three_var(v)
x = v(1);
y = v(2);
z = v(3);
b = x.^2 + 2.5*sin(y) - z^2*x^2*y^2;Ahora, encuentre un mínimo para esta función utilizando x = -0.6, y = -1.2 y z = 0.135 como los valores de inicio.
v = [-0.6,-1.2,0.135]; a = fminsearch(@three_var,v)
a =
0.0000 -1.5708 0.1803Nota
Los solvers de optimización se aplican a funciones con valor real. Los valores complejos no se pueden optimizar, excepto para una función con valor real de los valores complejos, como la norma.
Maximizar funciones
Los solvers fminbnd y fminsearch intentan minimizar una función objetivo. Si tiene un problema de maximización, es decir, un problema con el formato
defina g(x) = –f(x) y minimice g.
Por ejemplo, para encontrar el máximo de tan(cos(x)) cercano a x = 5, evalúe:
[x fval] = fminbnd(@(x)-tan(cos(x)),3,8)
x =
6.2832
fval =
-1.5574El máximo es 1.5574 (el negativo del fval indicado) y se produce en x = 6.2832. Esta respuesta es correcta, ya que, para cinco dígitos, el máximo es tan(1) = 1.5574, que se produce en x = 2π = 6.2832.
Algoritmo fminsearch
fminsearch utiliza el algoritmo simplex de Nelder-Mead, como se describe en Lagarias et al. [1]. Este algoritmo utiliza un simplex de n + 1 puntos para vectores x de n dimensiones. Primero, el algoritmo realiza un simplex alrededor de la conjetura inicial x0 añadiendo el 5% de cada componente x0(i) a x0. El algoritmo utiliza estos n vectores como elementos del simplex, además de x0. (El algoritmo utiliza 0.00025 como componente i si x0(i) = 0). Después, el algoritmo modifica el simplex de forma repetida según el siguiente procedimiento.
Nota
Las palabras clave para la visualización iterativa de fminsearch aparecen en negrita después de la descripción del paso.
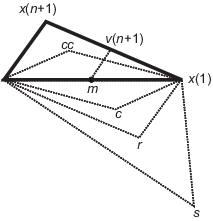
Deje que x(i) exprese la lista de puntos del simplex actual, i = 1,...,n + 1.
Ordene los puntos del simplex del valor de función más bajo f(x(1)) al más alto f(x(n + 1)). En cada paso de la iteración, el algoritmo descarta el peor punto actual x(n + 1) y acepta otro punto en el simplex [o, en el caso del paso 7 siguiente, cambia todos los n puntos con valores superiores a f(x(1))].
Genere el punto reflejado
r = 2m – x(n + 1), (1) donde
m = Σx(i)/n, i = 1...n, (2) y calcule f(r).
Si f(x(1)) ≤ f(r) < f(x(n)), acepte r y termine esta iteración. Reflejar
Si f(r) < f(x(1)), calcule el punto de expansión s
s = m + 2(m – x(n + 1)), (3) y calcule f(s).
Si f(s) < f(r), acepte s y termine la iteración. Expandir
De lo contrario, acepte r y termine la iteración. Reflejar
Si f(r) ≥ f(x(n)), realice una contracción entre m y x(n + 1) o r, dependiendo de cuál tenga el valor de función objetivo más bajo.
Si f(r) < f(x(n + 1)) (es decir, r es mejor que x(n + 1)), calcule
c = m + (r – m)/2 (4) y calcule f(c). Si f(c) < f(r), acepte c y termine la iteración. Contraer fuera
De lo contrario, continúe con el paso 7 (Reducir).
Si f(r) ≥ f(x(n + 1)), calcule
cc = m + (x(n + 1) – m)/2 (5) y calcule f(cc). Si f(cc) < f(x(n + 1)), acepte cc y termine la iteración. Contraer dentro
De lo contrario, continúe con el paso 7 (Reducir).
Calcule los n puntos
v(i) = x(1) + (x(i) – x(1))/2 (6) y calcule f(v(i)), i = 2,...,n + 1. El simplex en la siguiente iteración es x(1), v(2),...,v(n + 1). Reducir
La siguiente figura muestra los puntos que puede calcular fminsearch en el procedimiento, junto con cada nuevo simplex posible. El simplex original tiene un contorno resaltado. Las iteraciones continúan hasta que cumplen un criterio de parada.
Referencia
[1] Lagarias, J. C., J. A. Reeds, M. H. Wright, and P. E. Wright. “Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions.” SIAM Journal of Optimization, Vol. 9, Number 1, 1998, pp. 112–147.