La traducción de esta página aún no se ha actualizado a la versión más reciente. Haga clic aquí para ver la última versión en inglés.

bessely

Función de Bessel de segunda especie

Sintaxis

Y = bessely(nu,Z)

Y = bessely(nu,Z,scale)

Descripción

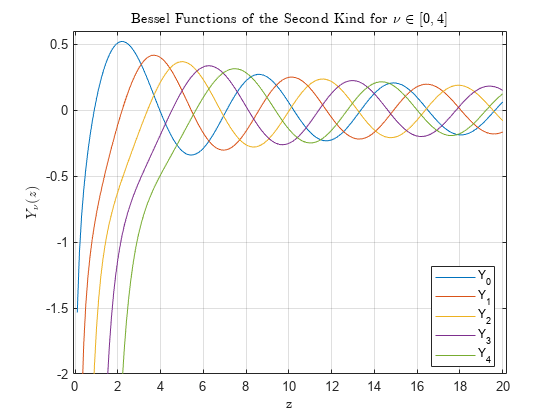
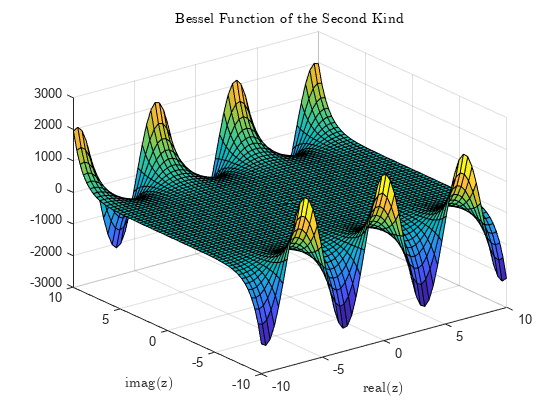
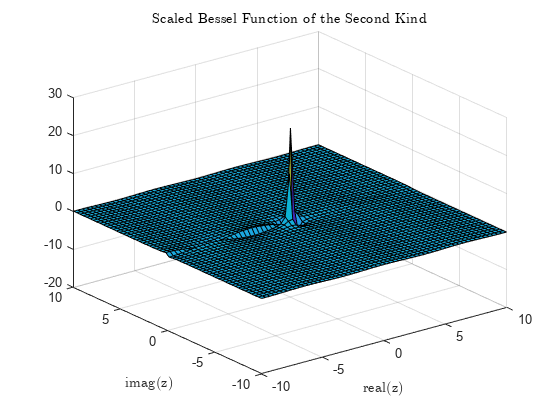
Y = bessely(nu,Z) calcula la función de Bessel de segunda especie Y_ν(z) para cada elemento del arreglo Z.

Y = bessely(nu,Z,scale) especifica si se debe escalar exponencialmente la función de Bessel de segunda especie para evitar el desbordamiento o la pérdida de precisión. Si scale es 1, la salida de bessely se escala por el factor exp(-abs(imag(Z))).

Ejemplos

Representar funciones de Bessel de segunda especie

Defina el dominio.

z = 0:0.1:20;

Calcule las primeras cinco funciones de Bessel de segunda especie. Cada fila de Y contiene los valores de un orden de la función evaluada en los puntos de z.

Y = zeros(5,201);
for i = 0:4
    Y(i+1,:) = bessely(i,z);
end

Represente todas las funciones en la misma figura.

plot(z,Y)
axis([-0.1 20.2 -2 0.6])
grid on
legend('Y_0','Y_1','Y_2','Y_3','Y_4','Location','Best')
title('Bessel Functions of the Second Kind for $\nu \in [0, 4]$','interpreter','latex')
xlabel('z','interpreter','latex')
ylabel('$Y_\nu(z)$','interpreter','latex')

Calcular la función de Bessel escalada exponencialmente

Calcule la función de Bessel sin escalar (Y) y escalada (Ys) de segunda especie ${\mathit{Y}}_2\left(\mathit{z}\right)$ para valores complejos de $\mathit{z}$.

x = -10:0.35:10;
y = x';
z = x + 1i*y;
scale = 1;
Y = bessely(2,z);
Ys = bessely(2,z,scale);

Compare las gráficas de la parte imaginaria de las funciones escalada y sin escalar. Para valores grandes de abs(imag(z)), la función sin escalar desborda rápidamente los límites de precisión doble y deja de poder calcularse. La función escalada elimina este comportamiento exponencial dominante del cálculo, por lo que tiene un mayor rango de computabilidad en comparación con la función sin escalar.

surf(x,y,imag(Y))
title('Bessel Function of the Second Kind','interpreter','latex')
xlabel('real(z)','interpreter','latex')
ylabel('imag(z)','interpreter','latex')

surf(x,y,imag(Ys))
title('Scaled Bessel Function of the Second Kind','interpreter','latex')
xlabel('real(z)','interpreter','latex')
ylabel('imag(z)','interpreter','latex')

Argumentos de entrada

nu — Orden la de ecuación

escalar | vector | matriz | arreglo multidimensional

Orden la de ecuación, especificado como un escalar, un vector, una matriz o un arreglo multidimensional. nu es un número real que especifica el orden de la función de Bessel de segunda especie. nu y Z deben ser del mismo tamaño o uno de ellos puede ser un escalar.

Ejemplo: bessely(3,0:5)

Tipos de datos: single | double

Z — Dominio funcional

escalar | vector | matriz | arreglo multidimensional

Dominio funcional, especificado como escalar, vector, matriz o arreglo multidimensional. bessely es un valor real, donde Z es positivo. nu y Z deben ser del mismo tamaño o uno de ellos puede ser escalar.

Ejemplo: bessely(1,[1-1i 1+0i 1+1i])

Tipos de datos: single | double
Soporte de números complejos: Sí

scale — Activación o desactivación del escalado de la función

0 (predeterminado) | 1

Activación o desactivación del escalado de la función, especificada como uno de estos valores:

• 0 (predeterminado): sin escalado

• 1: escala la salida de bessely por exp(-abs(imag(Z)))

En el plano complejo, la magnitud de bessely crece rápidamente a medida que aumenta el valor de abs(imag(Z)), por lo que escalar exponencialmente la salida resulta útil para valores grandes de abs(imag(Z)) donde, de otro modo, los resultados pierden precisión rápidamente o desbordan los límites de la precisión doble.

Ejemplo: bessely(3,0:5,1)

Más acerca de

Funciones de Bessel

Esta ecuación diferencial, donde ν es una constante real, se denomina ecuación de Bessel:

$$z^2\frac{d^{2}y}{d{z}^2}+z\frac{dy}{dz}+\left(z^2-{\nu }^2\right)y=0.$$

Sus soluciones se conocen como funciones de Bessel.

Las funciones de Bessel de primera especie, indicadas como J_ν(z) y J_–ν(z), forman un conjunto de soluciones fundamental de la ecuación de Bessel para ν no entero. J_ν(z) está definida por

$$J_{\nu }(z)={\left(\frac{z}{2}\right)}^{\nu }{\displaystyle \sum }_{(k=0)}^{\infty }\frac{{\left(\frac{-z^2}{4}\right)}^k}{k!\Gamma (\nu +k+1)}.$$

Puede calcular las funciones de Bessel de primera especie con besselj.

Las funciones de Bessel de segunda especie, indicadas como Y_ν(z), forman una segunda solución de la ecuación de Bessel que es linealmente independiente de J_ν(z). Y_ν(z) está definida por

$$Y_{\nu }(z)=\frac{J_{\nu }(z)\cos (\nu \pi )-J_{-\nu }(z)}{\sin (\nu \pi )}.$$

Sugerencias

Las funciones de Bessel están relacionadas con las funciones de Hankel, también denominadas funciones de Bessel de tercera especie:

$$\begin{array}{l}{H}_{\nu }^{(1)}(z)=J_{\nu }(z)+i{Y}_{\nu }(z)\\ H_{\nu }^{(2)}(z)=J_{\nu }(z)-i{Y}_{\nu }(z).\end{array}$$

$$H_{\nu }^{(K)}(z)$$ es besselh, J_ν(z) es besselj y Y_ν(z) es bessely. Las funciones de Hankel también forman un conjunto de soluciones fundamental de la ecuación de Bessel (consulte besselh).

Referencias

[1] Amos, D. E. “Algorithm 644: A Portable Package for Bessel Functions of a Complex Argument and Nonnegative Order.” ACM Transactions on Mathematical Software 12, no. 3 (September 1986): 265–273. https://dl.acm.org/doi/10.1145/7921.214331.

Capacidades ampliadas

Arreglos altos

Realice cálculos con arreglos que tienen más filas de las que caben en la memoria.

La función bessely es totalmente compatible con los arreglos altos. Para obtener más información, consulte Arreglos altos.

Generación de código C/C++

Genere código C y C++ mediante MATLAB® Coder™.

Notas y limitaciones de uso:

• Siempre devuelve un resultado complejo.

• Los cálculos de precisión simple estricta no son compatibles. En el código generado, las entradas de precisión simple producen salidas de precisión simple. No obstante, las variables dentro de la función pueden ser de doble precisión.

Generación de código de GPU

Genere código CUDA® para GPU NVIDIA® mediante GPU Coder™.

Notas y limitaciones de uso:

• Siempre devuelve un resultado complejo.

• Los cálculos de precisión simple estricta no son compatibles. En el código generado, las entradas de precisión simple producen salidas de precisión simple. No obstante, las variables dentro de la función pueden ser de doble precisión.

Entorno basado en subprocesos

Ejecute código en segundo plano con MATLAB® backgroundPool o acelere código con Parallel Computing Toolbox™ ThreadPool.

Esta función es totalmente compatible con entornos basados en subprocesos. Para obtener más información, consulte Ejecutar funciones de MATLAB en entornos basados en subprocesos.

Arreglos GPU

Acelere código mediante la ejecución en una unidad de procesamiento gráfico (GPU) mediante Parallel Computing Toolbox™.

La función bessely es compatible con entradas de arreglos de GPU con estas notas y limitaciones de uso:

• El orden nu debe contener valores enteros reales no negativos.

• El argumento Z debe contener valores reales no negativos.

Para obtener más información, consulte Run MATLAB Functions on a GPU (Parallel Computing Toolbox).

Arreglos distribuidos

Realice particiones de arreglos grandes por toda la memoria combinada de su cluster mediante Parallel Computing Toolbox™.

Esta función es totalmente compatible con los arreglos distribuidos. Para obtener más información, consulte Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).

Historial de versiones

Introducido antes de R2006a

Consulte también

besselh | besseli | besselj | besselk