ellipsoid

Create ellipsoid

Syntax

[X,Y,Z] = ellipsoid(xc,yc,zc,xr,yr,zr)

[X,Y,Z] = ellipsoid(xc,yc,zc,xr,yr,zr,n)

ellipsoid(___)

ellipsoid(___,Name=Value)

ellipsoid(ax,___)

Description

Create Ellipsoid Data

[X,Y,Z] = ellipsoid(xc,yc,zc,xr,yr,zr) returns the x-, y-, and z-coordinates of an ellipsoid without drawing it. The returned ellipsoid has center coordinates at (xc,yc,zc), semiaxis lengths (xr,yr,zr), and consists of 20-by-20 faces.

The function returns the x-, y-, and z- coordinates as three 21-by-21 matrices.

To draw the ellipsoid using the returned coordinates, use the surf or mesh functions.

[X,Y,Z] = ellipsoid(xc,yc,zc,xr,yr,zr,n) returns the x-, y-, and z-coordinates of an ellipsoid with n-by-n faces. The function returns the x-, y-, and z-coordinates as three (n+1)-by-(n+1) matrices.

Plot Ellipsoids

ellipsoid(___) plots the ellipsoid without returning the coordinates. Use this syntax with any of the previous input arguments in previous syntaxes.

ellipsoid(___,Name=Value) sets properties of the ellipsoid plot using one or more name-value arguments. For example, you can specify the color and transparency of the ellipsoid. For a list of properties, see Surface Properties. (since R2024b)

ellipsoid(ax,___) plots into the axes specified by ax instead of the current axes. Specify the axes as the first input argument.

Examples

Create and Display Ellipsoid

Create and plot an ellipsoid with a center at (0, –0.5, 0) and semiaxis lengths (6, 3.25, 3.25). Use axis equal to use equal data units along each coordinate direction.

ellipsoid(0,-0.5,0,6,3.25,3.25)
axis equal

Apply Translation and Rotation to Ellipsoid

Generate coordinates of an ellipsoid with a center at (0, 0, 0) and semiaxis lengths (1.5, 1.5, 3).

[X,Y,Z] = ellipsoid(0,0,0,1.5,1.5,3);

Create a surface plot of the ellipsoid.

surf(X,Y,Z);
axis equal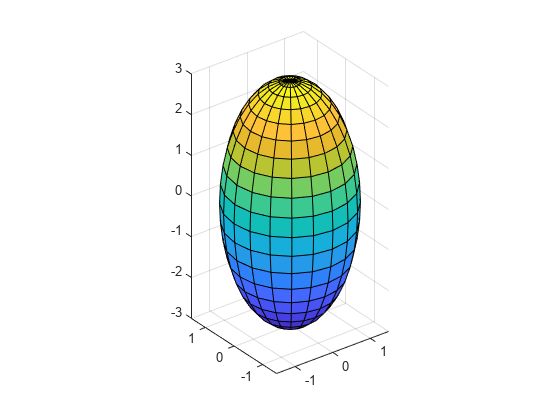

Plot a second ellipsoid with its center translated by (3, 0, 5) from the first ellipsoid. To be able to rotate the second ellipsoid in the next step, return the surface object as s.

hold on
s = surf(X+3,Y,Z+5);

Rotate the second ellipsoid by 45 degrees around its $$x$$-axis. The new coordinates of the translated and rotated ellipsoid are stored in s.Xdata, s.Ydata, and s.Zdata.

direction = [1 0 0];
rotate(s,direction,45)

Display Ellipsoids with Different Numbers of Faces

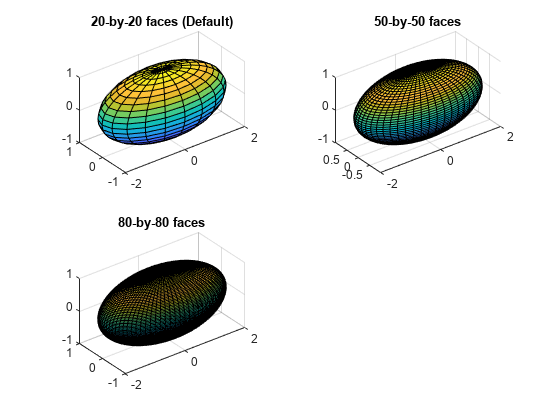
Display ellipsoids with center coordinates (0, 0, 0) and semiaxis lengths (2, 1, 1) with different number of faces.

Call the tiledlayout function to create a 2-by-2 tiled chart layout. Call the nexttile function to create the axes. Then, use the ellipsoid function to plot three ellipsoids with different numbers of faces. Plot the ellipsoids in different tiles of the chart by specifying the axes.

tiledlayout(2,2);
ax1 = nexttile;
ellipsoid(ax1,0,0,0,2,1,1)
axis equal
title('20-by-20 faces (Default)')

ax2 = nexttile;
ellipsoid(ax2,0,0,0,2,1,1,50)
axis equal
title('50-by-50 faces')

ax3 = nexttile;
ellipsoid(ax3,0,0,0,2,1,1,80)
axis equal
title('80-by-80 faces')

Input Arguments

xc,yc,zc — Coordinates of ellipsoid center

three comma-separated scalar numbers

Coordinates of ellipsoid center, specified as three comma-separated scalar numbers.

Data Types: single | double | duration | datetime

xr,yr,zr — Principal semiaxes along x-, y-, and z-axes

three comma-separated scalar numbers

Principal semiaxes along the x-, y-, and z-axes, specified as three comma-separated scalar numbers.

Data Types: single | double

n — Number of faces

positive scalar integer

Number of faces, specified as a positive scalar integer.

ax — Target axes

Axes object

Target axes, specified as an Axes object. If you do not specify the axes, then ellipsoid plots into the current axes.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: ellipsoid(0,0,0,2,1,1,FaceAlpha=0.5) plots an ellipsoid that is 50% transparent.

Note

The properties listed here are only a subset. For a full list, see Surface Properties.

FaceColor — Face color

'flat' (default) | 'interp' | 'none' | 'texturemap' | RGB triplet | hexadecimal color code | 'r' | 'g' | 'b' | ...

Face color, specified as one of the values in this table.

Value	Description
'flat'	Use a different color for each face based on the values in the CData property. First you must specify the CData property as a matrix the same size as ZData. The color value at the first vertex of each face (in the positive x and y directions) determines the color for the entire face. You cannot use this value when the FaceAlpha property is set to 'interp'.
'interp'	Use interpolated coloring for each face based on the values in the CData property. First you must specify the CData property as a matrix the same size as ZData. The color varies across each face by interpolating the color values at the vertices. You cannot use this value when the FaceAlpha property is set to 'flat'.
RGB triplet, hexadecimal color code, or color name	Use the specified color for all the faces. This option does not use the color values in the CData property.
'texturemap'	Transform the color data in CData so that it conforms to the surface.
'none'	Do not draw the faces.

RGB triplets and hexadecimal color codes are useful for specifying custom colors.

• An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1]; for example, [0.4 0.6 0.7].

• A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Thus, the color codes "#FF8800", "#ff8800", "#F80", and "#f80" are equivalent.

Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.

Color Name	Short Name	RGB Triplet	Hexadecimal Color Code	Appearance
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"

Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB^® uses in many types of plots.

RGB Triplet	Hexadecimal Color Code	Appearance
[0 0.4470 0.7410]	"#0072BD"
[0.8500 0.3250 0.0980]	"#D95319"
[0.9290 0.6940 0.1250]	"#EDB120"
[0.4940 0.1840 0.5560]	"#7E2F8E"
[0.4660 0.6740 0.1880]	"#77AC30"
[0.3010 0.7450 0.9330]	"#4DBEEE"
[0.6350 0.0780 0.1840]	"#A2142F"

FaceAlpha — Face transparency

1 (default) | scalar in range [0,1] | 'flat' | 'interp' | 'texturemap'

Face transparency, specified as one of these values:

• Scalar in range [0,1] — Use uniform transparency across all the faces. A value of 1 is fully opaque and 0 is completely transparent. Values between 0 and 1 are semitransparent. This option does not use the transparency values in the AlphaData property.

• 'flat' — Use a different transparency for each face based on the values in the AlphaData property. The transparency value at the first vertex determines the transparency for the entire face. First you must specify the AlphaData property as a matrix the same size as the ZData property. The FaceColor property also must be set to 'flat'.

• 'interp' — Use interpolated transparency for each face based on the values in AlphaData property. The transparency varies across each face by interpolating the values at the vertices. First you must specify the AlphaData property as a matrix the same size as the ZData property. The FaceColor property also must be set to 'interp'.

• 'texturemap' — Transform the data in AlphaData so that it conforms to the surface.

EdgeColor — Edge line color

[0 0 0] (default) | 'none' | 'flat' | 'interp' | RGB triplet | hexadecimal color code | 'r' | 'g' | 'b' | ...

Edge line color, specified as one of the values listed here. The default color of [0 0 0] corresponds to black edges.

Value	Description
'none'	Do not draw the edges.
'flat'	Use a different color for each edge based on the values in the CData property. First you must specify the CData property as a matrix the same size as ZData. The color value at the first vertex of each face (in the positive x and y directions) determines the color for the adjacent edges. You cannot use this value when the EdgeAlpha property is set to 'interp'.
'interp'	Use interpolated coloring for each edge based on the values in the CData property. First you must specify the CData property as a matrix the same size as ZData. The color varies across each edge by linearly interpolating the color values at the vertices. You cannot use this value when the EdgeAlpha property is set to 'flat'.
RGB triplet, hexadecimal color code, or color name	Use the specified color for all the edges. This option does not use the color values in the CData property.

RGB triplets and hexadecimal color codes are useful for specifying custom colors.

• An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1]; for example, [0.4 0.6 0.7].

• A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Thus, the color codes "#FF8800", "#ff8800", "#F80", and "#f80" are equivalent.

Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.

Color Name	Short Name	RGB Triplet	Hexadecimal Color Code	Appearance
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"

Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.

RGB Triplet	Hexadecimal Color Code	Appearance
[0 0.4470 0.7410]	"#0072BD"
[0.8500 0.3250 0.0980]	"#D95319"
[0.9290 0.6940 0.1250]	"#EDB120"
[0.4940 0.1840 0.5560]	"#7E2F8E"
[0.4660 0.6740 0.1880]	"#77AC30"
[0.3010 0.7450 0.9330]	"#4DBEEE"
[0.6350 0.0780 0.1840]	"#A2142F"

EdgeColor — Edge line color

[0 0 0] (default) | 'none' | 'flat' | 'interp' | RGB triplet | hexadecimal color code | 'r' | 'g' | 'b' | ...

Edge line color, specified as one of the values listed here. The default color of [0 0 0] corresponds to black edges.

Value	Description
'none'	Do not draw the edges.
'flat'	Use a different color for each edge based on the values in the CData property. First you must specify the CData property as a matrix the same size as ZData. The color value at the first vertex of each face (in the positive x and y directions) determines the color for the adjacent edges. You cannot use this value when the EdgeAlpha property is set to 'interp'.
'interp'	Use interpolated coloring for each edge based on the values in the CData property. First you must specify the CData property as a matrix the same size as ZData. The color varies across each edge by linearly interpolating the color values at the vertices. You cannot use this value when the EdgeAlpha property is set to 'flat'.
RGB triplet, hexadecimal color code, or color name	Use the specified color for all the edges. This option does not use the color values in the CData property.

RGB triplets and hexadecimal color codes are useful for specifying custom colors.

• An RGB triplet is a three-element row vector whose elements specify the intensities of the red, green, and blue components of the color. The intensities must be in the range [0,1]; for example, [0.4 0.6 0.7].

• A hexadecimal color code is a character vector or a string scalar that starts with a hash symbol (#) followed by three or six hexadecimal digits, which can range from 0 to F. The values are not case sensitive. Thus, the color codes "#FF8800", "#ff8800", "#F80", and "#f80" are equivalent.

Alternatively, you can specify some common colors by name. This table lists the named color options, the equivalent RGB triplets, and hexadecimal color codes.

Color Name	Short Name	RGB Triplet	Hexadecimal Color Code	Appearance
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"

Here are the RGB triplets and hexadecimal color codes for the default colors MATLAB uses in many types of plots.

RGB Triplet	Hexadecimal Color Code	Appearance
[0 0.4470 0.7410]	"#0072BD"
[0.8500 0.3250 0.0980]	"#D95319"
[0.9290 0.6940 0.1250]	"#EDB120"
[0.4940 0.1840 0.5560]	"#7E2F8E"
[0.4660 0.6740 0.1880]	"#77AC30"
[0.3010 0.7450 0.9330]	"#4DBEEE"
[0.6350 0.0780 0.1840]	"#A2142F"

EdgeAlpha — Edge transparency

1 (default) | scalar value in range[0,1] | 'flat' | 'interp'

Edge transparency, specified as one of these values:

• Scalar in range [0,1] — Use uniform transparency across all of the edges. A value of 1 is fully opaque and 0 is completely transparent. Values between 0 and 1 are semitransparent. This option does not use the transparency values in the AlphaData property.

• 'flat' — Use a different transparency for each edge based on the values in the AlphaData property. First you must specify the AlphaData property as a matrix the same size as the ZData property. The transparency value at the first vertex determines the transparency for the entire edge. The EdgeColor property also must be set to 'flat'.

• 'interp' — Use interpolated transparency for each edge based on the values in AlphaData property. First you must specify the AlphaData property as a matrix the same size as the ZData property. The transparency varies across each edge by interpolating the values at the vertices. The EdgeColor property also must be set to 'interp'.

Algorithms

ellipsoid generates the data using this equation:

$$\frac{{\left(x-xc\right)}^2}{x{r}^2}+\frac{{\left(y-yc\right)}^2}{y{r}^2}+\frac{{\left(z-zc\right)}^2}{z{r}^2}=1.$$

ellipsoid(0,0,0,1,1,1) is equivalent to a unit sphere.

Version History

Introduced before R2006a

R2024b: Control appearance and behavior with name-value arguments

Control the appearance and behavior of ellipsoid plots by specifying name-value arguments. Previously, ellipsoid did not support name-value arguments.