mat2cell

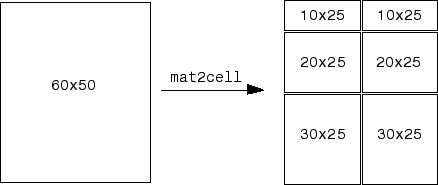
Convertir un arreglo a un arreglo de celdas, cuyas celdas contienen subarreglos

contraer todo en la página

Sintaxis

C = mat2cell(A,dim1Dist,...,dimNDist)
C = mat2cell(A,rowDist)

Descripción

C = mat2cell(A,dim1Dist,...,dimNDist) divide el arreglo A en arreglos más pequeños y los devuelve en un arreglo de celdas C. Los vectores dim1Dist,...dimNDist especifican cómo dividir las filas, columnas y las dimensiones más altas de A cuando corresponda. Los arreglos más pequeños en C pueden tener diferentes tamaños. A puede tener cualquier tipo de datos.

ejemplo

C = mat2cell(A,rowDist) divide el arreglo A en un arreglo de celdas C de n por 1, donde n es igual al número de elementos en rowDist.

ejemplo

Ejemplos

contraer todo

Abrir script en vivo

Cree un arreglo numérico de 5᠐ por 4.

A = reshape(1:20,5,4)'
A = 4×5

     1     2     3     4     5
     6     7     8     9    10
    11    12    13    14    15
    16    17    18    19    20

Divida A en dos subarreglos de 2 por 3 y dos de 2 por 2. Devuelva los subarreglos en un arreglo de celdas.

C = mat2cell(A,[2 2],[3 2])
C=2×2 cell array
    {2×3 double}    {2×2 double}
    {2×3 double}    {2×2 double}

Muestre los subarreglos en C con la función celldisp.

celldisp(C)
 
C{1,1} =
 
     1     2     3
     6     7     8

 
 
C{2,1} =
 
    11    12    13
    16    17    18

 
 
C{1,2} =
 
     4     5
     9    10

 
 
C{2,2} =
 
    14    15
    19    20
Abrir script en vivo

Cree un arreglo.

A = reshape(1:20,5,4)'
A = 4×5

     1     2     3     4     5
     6     7     8     9    10
    11    12    13    14    15
    16    17    18    19    20

Divida las columnas de A para que el arreglo de celdas contenga dos subarreglos. Dado que el primer elemento de rowDist es 1, la primera celda de C contiene la primera fila de A. El segundo elemento de rowDist es 3; por lo que la siguiente celda de C contiene las siguientes tres filas de A. La suma de los elementos de rowDist debe ser igual al número de filas de A.

rowDist = [1 3];
C = mat2cell(A,rowDist)
C=2×1 cell array
    {[1 2 3 4 5]}
    {3×5 double }

Muestre los subarreglos.

celldisp(C)
 
C{1} =
 
     1     2     3     4     5

 
 
C{2} =
 
     6     7     8     9    10
    11    12    13    14    15
    16    17    18    19    20

Argumentos de entrada

contraer todo

Arreglo de entrada.

Vectores que describen las distribuciones de los elementos del arreglo de entrada en cada dimensión, especificados como vectores numéricos.

Por ejemplo, si A es un arreglo de 60 por 50, podrá especificar este argumento como [10 20 30],[25 25] para dividir A, como se muestra en el código y figura. C es un arreglo de celdas que contiene los seis subarreglos extraídos de A.

C = mat2cell(A,[10 20 30],[25 25])

Para la K-ésima dimensión de A, especifique los elementos del vector dimKDist correspondiente, de manera que sum(dimKDist) sea igual al tamaño de la K-ésima dimensión.

Si la K-ésima dimensión de A tiene un tamaño de cero, especifique el vector dimKDist correspondiente como el arreglo vacío, [], tal y como se muestra en el código.

A = rand(3,0,4);
C = mat2cell(A,[1 2],[],[2 1 1]);

Vector que describe la distribución por filas del arreglo de entrada, especificado como vector numérico. Cuando no especifica cómo dividir A en cualquier otra dimensión, la función mat2cell devuelve un arreglo de celdas C de n por 1, donde n es igual al número de elementos en rowDist.

Cada elemento de rowDist especifica el número de filas en el subarreglo que están en la celda correspondiente de C. La suma de los elementos de rowDist debe ser igual al número de filas de A.

Capacidades ampliadas

expandir todo

Historial de versiones

Introducido antes de R2006a

Consulte también

|

Temas