Esta página se ha traducido mediante traducción automática. Haga clic aquí para ver la última versión en inglés.

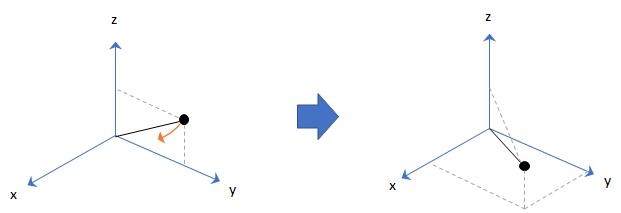
punto de rotación

Rotación del punto cuaternión

Sintaxis

rotationResult = rotatepoint(quat,cartesianPoints)

Descripción

rotationResult = rotatepoint(quat,cartesianPoints) rota los puntos cartesianos utilizando el cuaternión, quat. Los elementos del cuaternión se normalizan antes de su uso en la rotación.

Ejemplos

Rotar punto usando el vector cuaternión

Definir un punto en tres dimensiones. Las coordenadas de un punto siempre se especifican en orden x, y, z. Para una visualización conveniente, defina el punto en el plano x-y.

x = 0.5;
y = 0.5;
z = 0;

plot(x,y,"ko")
hold on
axis([-1 1 -1 1])

Crea un vector de cuaternión que especifique dos rotaciones separadas, una para rotar el punto 45 y otra para rotar el punto -90 grados alrededor del eje z. Utilice rotatepoint para realizar la rotación.

quat = quaternion([0,0,pi/4; ...
                   0,0,-pi/2],"euler","XYZ","point");
               
rotatedPoint = rotatepoint(quat,[x,y,z])

rotatedPoint = 2×3

   -0.0000    0.7071         0
    0.5000   -0.5000         0

Traza los puntos rotados.

plot(rotatedPoint(1,1),rotatedPoint(1,2),"bo")
plot(rotatedPoint(2,1),rotatedPoint(2,2),"go")

Rotar grupo de puntos usando cuaternión

Defina dos puntos en un espacio tridimensional. Define un cuaternión para rotar el punto girando primero sobre el eje z 30 grados y luego sobre el nuevo eje y 45 grados.

a = [1,0,0];
b = [0,1,0];
quat = quaternion([30,45,0],"eulerd","ZYX","point");

Utilice rotatepoint para rotar ambos puntos utilizando el operador de rotación de cuaternión. Muestra el resultado.

rP = rotatepoint(quat,[a;b])

rP = 2×3

    0.6124    0.5000   -0.6124
   -0.3536    0.8660    0.3536

Visualice la orientación original y la orientación rotada de los puntos. Dibuja líneas desde el origen hasta cada uno de los puntos para fines de visualización.

plot3(a(1),a(2),a(3),"bo");

hold on
grid on
axis([-1 1 -1 1 -1 1])
xlabel("x")
ylabel("y")
zlabel("z")

plot3(b(1),b(2),b(3),"ro")
plot3(rP(1,1),rP(1,2),rP(1,3),"bd")
plot3(rP(2,1),rP(2,2),rP(2,3),"rd")

plot3([0;rP(1,1)],[0;rP(1,2)],[0;rP(1,3)],"k")
plot3([0;rP(2,1)],[0;rP(2,2)],[0;rP(2,3)],"k")
plot3([0;a(1)],[0;a(2)],[0;a(3)],"k")
plot3([0;b(1)],[0;b(2)],[0;b(3)],"k")

Argumentos de entrada

quat — Cuaternión que define la rotación

objeto quaternion | vector de objetos quaternion

Cuaternión que define la rotación, especificado como un objeto quaternion o un vector de objetos quaternion. quat y cartesianPoints deben tener tamaños compatibles:

• length(quat) == size(cartesianPoints,1), o

• length(quat) == 1, o

• size(cartesianPoints,1) == 1

cartesianPoints — Puntos cartesianos tridimensionales

vector numérico de 1 por 3 | matriz numérica de N por 3

Puntos cartesianos tridimensionales, especificados como un vector numérico de 1 por 3 que representa un solo punto o una matriz numérica de N por 3 que representa puntos N. quat y cartesianPoints deben tener tamaños compatibles:

• length(quat) == size(cartesianPoints,1) o

• length(quat) == 1, o

• size(cartesianPoints,1) == 1

Tipos de datos: single | double

Argumentos de salida

rotationResult — Puntos cartesianos reposicionados

vector numérico de 1 por 3 | matriz numérica

Puntos cartesianos rotados definidos mediante la rotación de cuaterniones, devueltos como un vector numérico de 1 por 3 o una matriz numérica.

rotationResult es un vector de 1 por 3 cuando quat es un objeto escalar quaternion y cartesianPoints es un vector de 1 por 3 que representa un solo punto. De lo contrario, rotationResult es una matriz de M por 3, donde M es el máximo de length(quat) y size(cartesianPoints,1).

Tipos de datos: single | double

Algoritmos

La rotación del punto cuaternión gira un punto especificado en R³ según un cuaternión especificado:

$$L_q(u)=qu{q}^{*}$$

donde q es el cuaternión, * representa la conjugación y u es el punto a rotar, especificado como un cuaternión.

Para mayor comodidad, la función rotatepoint toma un punto en R³ y devuelve un punto en R³. Dada una llamada de función con un cuaternión arbitrario, q = a + bi + cj + dk, y una coordenada arbitraria, [x,y,z], por ejemplo,

rereferencedPoint = rotatepoint(q,[x,y,z])

La función rotatepoint realiza las siguientes operaciones:

1. Convierte el punto [x,y,z] en un cuaternión:

   $$u_q=0+xi+yj+zk$$

2. Normaliza el cuaternión, q:

   $$q_n=\frac{q}{\sqrt{a^2+b^2+c^2+d^2}}$$

3. Aplica la rotación:

   $$v_q=q{u}_q{q}^{*}$$

4. Convierte la salida del cuaternión, v_q, de nuevo a R³

Capacidades ampliadas

Generación de código C/C++
Genere código C y C++ mediante MATLAB® Coder™.

Historial de versiones

Introducido en R2019b

Consulte también

Funciones

• rotateframe

Objetos

• quaternion

Temas

• Rotaciones, orientación y cuaterniones